The MDC Procedure
Nested Logit Modeling
A more general model can be specified using the nested logit model.
Consider, for example, the following random utility function:
![\[ U_{ij} = {x}_{ij}\beta + \epsilon _{ij}\; \; j=1,\ldots ,3 \]](images/etsug_mdc0014.png)
Suppose the set of all alternatives indexed by j is partitioned into K nests,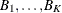 
. The nested logit model is obtained by assuming that the error term in the utility function has the GEV cumulative distribution
function
![\[ \exp \left(-\sum _{k=1}^ K\left(\sum _{j\in B_ k}\exp \{ -\epsilon _{ij}/\lambda _ k\} \right)^{\lambda _ k}\right) \]](images/etsug_mdc0016.png)
where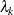 
is a measure of a degree of independence among the alternatives in nest k. When 
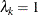for all k, the model reduces to the standard logit model.
Since the public transportation modes, 1 and 2, tend to be correlated, these two choices can be grouped together. The decision tree displayed in Figure 25.8 is constructed.
Figure 25.8: Decision Tree for Model Choice
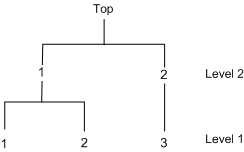
The two-level decision tree is specified in the NEST statement. The NCHOICE= option is not allowed for nested logit estimation. Instead, the CHOICE= option needs to be specified, as in the following statements:
/*-- nested logit estimation --*/
proc mdc data=newdata;
model decision = ttime /
type=nlogit
choice=(mode 1 2 3)
covest=hess;
id pid;
utility u(1,) = ttime;
nest level(1) = (1 2 @ 1, 3 @ 2),
level(2) = (1 2 @ 1);
run;
In Figure 25.9, estimates of the inclusive value parameters, INC_L2G1C1 and INC_L2G1C2, are indicative of a nested model structure. See the section Nested Logit and the section Decision Tree and Nested Logit for more details about inclusive values.
Figure 25.9: Two-Level Nested Logit Estimates
The nested logit model is estimated with the restriction INC_L2G1C1 = INC_L2G1C2 by specifying the SAMESCALE option, as in the following statements:
/*-- nlogit with samescale option --*/
proc mdc data=newdata;
model decision = ttime /
type=nlogit
choice=(mode 1 2 3)
samescale
covest=hess;
id pid;
utility u(1,) = ttime;
nest level(1) = (1 2 @ 1, 3 @ 2),
level(2) = (1 2 @ 1);
run;
The estimation result is displayed in Figure 25.10.
Figure 25.10: Nested Logit Estimates with One Dissimilarity Parameter
The nested logit model is equivalent to the conditional logit model if INC_L2G1C1 = INC_L2G1C2 = 1. You can verify this relationship by estimating a constrained nested logit model as shown in the following statements.
(See the section RESTRICT Statement for details about imposing linear restrictions on parameter estimates.)
/*-- constrained nested logit estimation --*/
proc mdc data=newdata;
model decision = ttime /
type=nlogit
choice=(mode 1 2 3)
covest=hess;
id pid;
utility u(1,) = ttime;
nest level(1) = (1 2 @ 1, 3 @ 2),
level(2) = (1 2 @ 1);
restrict INC_L2G1C1 = 1, INC_L2G1C2 =1;
run;
The parameter estimates and the active linear constraints for the constrained nested logit model are displayed in Figure 25.11.
Figure 25.11: Constrained Nested Logit Estimates
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
Parameter Label |
| ttime_L1 | 1 | -0.3572 | 0.0776 | -4.60 | <.0001 | |
| INC_L2G1C1 | 0 | 1.0000 | 0 | |||
| INC_L2G1C2 | 0 | 1.0000 | 0 | |||
| Restrict1 | 1 | -2.1706 | 8.4098 | -0.26 | 0.7993* | Linear EC [ 1 ] |
| Restrict2 | 1 | 3.6573 | 10.0001 | 0.37 | 0.7186* | Linear EC [ 2 ] |
| * Probability computed using beta distribution. |