The TIMESERIES Procedure

Spectral Density Analysis

Using Kernel Specifications
Using Specification of Weight Constants
Computational Method
Missing Values

Spectral analysis can be performed on the working series by specifying the OUTSPECTRA= option or by specifying the PLOTS=PERIODOGRAM or PLOTS=SPECTRUM option in the PROC TIMESERIES statement. PROC TIMESERIES uses the finite Fourier transform to decompose data series into a sum of sine and cosine terms of different amplitudes and wavelengths. The finite Fourier transform decomposition of the series is

$\displaystyle x_ t$	$\displaystyle = \frac{a_0}{2} + \sum _{k=1}^{K-1}f_ k ( a_{k} \cos \omega _ kt +b_{k} \sin \omega _ kt )$
$\displaystyle f_ k$	$\displaystyle = \begin{cases} 1/2 & \textrm{if $T$ is even and $k=K-1$}\\ 1 & \textrm{otherwise} \end{cases}$

where

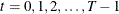
: is the time subscript, $t=0,1,2,\dots ,T-1$
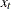
: are the equally spaced time series data
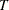
: is the number of observations in the time series
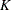
: is the number of frequencies in the Fourier decomposition: 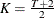$K=\frac{T+2}{2}$ if 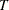is even, 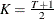$K=\frac{T+1}{2}$ if 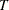is odd
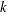
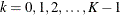
: is the frequency subscript, $k=0,1,2,\dots ,K-1$
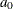
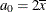
${a_{0}}$: is the mean term: ${a_{0} = 2 {\overline x}}$
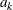
${a_{k}}$: are the cosine coefficients
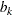
${b_{k}}$: are the sine coefficients
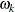
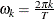
${{\omega }_{k}}$: are the Fourier frequencies: ${{\omega }_{k} = \frac{2{\pi }k}{T}}$

The Fourier decomposition is performed after the ACCUMULATE=, DIF=, SDIF= and TRANSFORM= options in the ID and VAR statements have been applied.

Functions of the Fourier coefficients ${a_{k}}$ and ${b_{k}}$ can be plotted against frequency or against wavelength to form periodograms. The amplitude periodogram ${I_{k}}$ is defined as follows:

$I_{k}=\frac{T}{2} ( a^{2}_{k}+ b^{2}_{k} )$

Since the Fourier transform is an even, periodic function of frequency which repeats every ordinates the periodogram is also. Values of for all therefore can be mapped to the unique values ${I_ k}:k = 0\ldots K-1$ using the equations

$\displaystyle I_ k$	$\displaystyle = I_{-k}$	$\displaystyle$	$\displaystyle \textrm{for all $k$}$
$\displaystyle I_ k$	$\displaystyle = I_{k+nT}$	$\displaystyle \qquad$	$\displaystyle \textrm{for $n = \pm 1, \pm 2, \pm 3, \ldots $}$
$\displaystyle I_ k$	$\displaystyle = I_{T-k}$	$\displaystyle$	$\displaystyle \textrm{for $0 \le k \le K-1$}$

The periodogram, , is an estimate at the discrete frequencies $\omega _ k$ of the spectral density function which characterizes the series . By smoothing the periodogram an improved spectral density estimate with reduced variance and bias can be achieved at these points. Smoothing can be accomplished either through use of a spectral window smoothing function or by applying a lag window filter to the series autocovariance function.

When the SPECTRA statement’s DOMAIN=FREQUENCY option is in effect spectral density estimates are computed by smoothing the periodogram ordinates using the equation

$\displaystyle S_{k}(M) = \sum _{\tau = K-T}^{K-1} {\textrm{w}\left( \frac{{\tau }}{M} \right) I_{k+\tau }}$

where $\mr {w}(\theta )$ is the spectral window function whose form is specified by either the KERNEL= option or the WEIGHTS option. is the kernel scale parameter which acts as a frequency scaling factor in the spectral window smoothing function. Values of $I_{k+\tau }$ that fall outside of $0 \le k + \tau \le K-1$ are mapped to values inside this range by the equations presented previously.

When the DOMAIN=TIME option is specified spectral density values are estimated by applying a lag window filter, $\lambda (h,M)$ , to the series autocovariance function. The spectral density estimate then can be computed from the filtered autocovariance function using the equation

$S_ k(M) = \sum _{h=-(T-1)}^{T-1} \lambda (h,M)\hat{\gamma }(h) \cos h\omega _ k.$

In this case the kernel scale parameter, , serves as a scale factor for the lag length, , in the time domain. In the lag window formulation the spectral density estimate is a consistent estimator as $T,M\to \infty$ under the conditions $\lambda (h,M) = 0$ for , and $\lim _{T\to \infty }M/T=0$ . These conditions lead to the following parameterization of provided by the SPECTRA statement:

$M = c K^ e$

where the values and satisfy the consistency conditions. To specify the kernel scale parameter explicitly, set to the desired scale factor and .

For uniformity and computational efficiency all spectral density estimates are calculated using a spectral window weighting function, $\textrm{w}(\theta )$ , applied to the periodogram ordinates. In the case where the DOMAIN=TIME option is specified the effective spectral window weighting function is computed by the equation

$\textrm{w}_\textrm {TIME}(\theta ) = \sum _{h=-(T-1)}^{T-1} \lambda (h,M) \cos h\theta .$

Because the kernel scale parameter, , serves as a lag scale factor in the time domain and bandwidth scale factor in the frequency domain the impact of on spectral density estimates depends on the value of the DOMAIN= option. When DOMAIN=FREQUENCY increasing values of decrease variance and increase bias in the spectral density estimates whereas when DOMAIN=TIME increasing values of increase variance and decrease bias.

Using Kernel Specifications

You can specify one of ten different kernel smoothing functions in the SPECTRA statement. Five smoothing functions are available as KERNEL= options and five complementary smoothing functions which correspond to lag window filters are available when the KERNEL= option is used in conjunction with the DOMAIN=TIME option.

For example, a Parzen kernel with a support of 11 periodogram ordinates in the frequency domain can be specified using the kernel option:

   spectra / parzen c=5 expon=0;

The TIMESERIES procedure supports the following spectral window kernel functions in the frequency domain where $x=\tau /M$ :

BARTLETT: Bartlett kernel

$\displaystyle \textrm{w}(x)$

$\displaystyle =$

$\displaystyle \begin{cases} 1-{|x|} & {|x|}{\le }1 \\ 0 & \mr {otherwise} \end{cases}$

PARZEN: Parzen kernel

$\displaystyle \textrm{w}(x)$

$\displaystyle =$

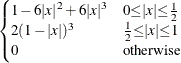$\displaystyle \begin{cases} 1-6{|x|}^{2} + 6{|x|}^{3} & {0{\le }{|x|}{\le }\frac{1}{2}} \\ 2(1-{|x|})^{3} & {\frac{1}{2}{\le }{|x|}{\le }1} \\ 0 & \mr {otherwise} \end{cases}$

QS: quadratic spectral kernel

$\displaystyle \mr {w}(x)$

$\displaystyle =$

$\displaystyle \frac{3}{(2\pi x)^2} \left( \frac{\sin 2\pi x}{2\pi x} - \cos 2\pi x \right)$

TUKEY: Tukey-Hanning kernel

$\displaystyle \textrm{w}(x)$

$\displaystyle =$

$\displaystyle \begin{cases} (1+\cos ( {\pi } x))/2 & {|x|}{\le }1 \\ 0 & \mr {otherwise} \end{cases}$

TRUNCAT: truncated kernel

$\displaystyle \textrm{w}(x)$

$\displaystyle =$

$\displaystyle \begin{cases} 1 & {|x|}{\le }1 \\ 0 & \mr {otherwise} \end{cases}$

When the DOMAIN=TIME option is specified the five kernel functions above are interpreted as lag window filters on the autocovariance function. The lag window kernel functions correspond to the following spectral window smoothing functions where $\theta =2\pi \tau /T$ :

BARTLETT: Bartlett equivalent lag window filter

$\displaystyle \textrm{w}(\theta )$

$\displaystyle =$

$\displaystyle \frac{1}{2\pi M}\left(\frac{\sin (M\theta /2)}{\sin (\theta /2)}\right)^2$

PARZEN: Parzen equivalent lag window filter

$\displaystyle \textrm{w}(\theta )$

$\displaystyle =$

$\displaystyle \frac{6}{\pi M^3}\left(\frac{\sin (M\theta /4)}{\sin (\theta /2)} \right)^4\left(1-\frac{2}{3}\sin ^2(\theta /2)\right)$

QS: quadratic spectral equivalent lag window filter

$\displaystyle \textrm{w}(\theta )$

$\displaystyle =$

$\displaystyle \begin{cases} \frac{3M}{4\pi }(1-(M\theta /\pi )^2) & {|\theta |}\le \pi /M \\ 0 & {|\theta |}>\pi /M \end{cases}$

TUKEY: Tukey-Hanning equivalent lag window filter

$\displaystyle \mr {w}(\theta )$	$\displaystyle =$	$\displaystyle \frac{1}{4}D_ M(\theta - \pi /M) + \frac{1}{2}D_ M(\theta ) + \frac{1}{4}D_ M(\theta + \pi /M)$
$\displaystyle D_ M(\theta )$	$\displaystyle =$	$\displaystyle \frac{1}{2\pi }\frac{\sin [(M+1/2)\theta ]}{\sin (\theta /2)}$

TRUNC: truncated equivalent lag window filter

$\displaystyle \mr {w}(\theta )$

$\displaystyle =$

$\displaystyle D_ M(\theta )$

Using Specification of Weight Constants

Any number of weighting constants can be specified. The constants are interpreted symmetrically about the middle weight. The middle constant (or the constant to the right of the middle if an even number of weight constants is specified) is the relative weight of the current periodogram ordinate. The constant immediately following the middle one is the relative weight of the next periodogram ordinate, and so on. The actual weights used in the smoothing process are the weights specified in the WEIGHTS option scaled so that they sum to 1.

The moving average calculation reflects at each end of the periodogram to accommodate the periodicity of the periodogram function.

For example, a simple triangular weighting can be specified using the following WEIGHTS option:

   spectra / weights 1 2 3 2 1;

Computational Method

If the number of observations, , factors into prime integers that are less than or equal to 23, and the product of the square-free factors of is less than 210, then the procedure uses the fast Fourier transform developed by Cooley and Tukey (1965) and implemented by Singleton (1969). If cannot be factored in this way, then the procedure uses a Chirp-Z algorithm similar to that proposed by Monro and Branch (1976).

Missing Values

Missing values are replaced with an estimate of the mean to perform spectral analyses. This treatment of a series with missing values is consistent with the approach used by Priestley (1981).