Table Analysis

Association in Sets of Tables

After the pilot study on the new ouchless Band-Aids, the investigators decided to continue their research by conducting a clinical trial in which children at five clinics were tested with the test and regular Band-Aids. Instead of a single table, the clinical trial produces five tables. In order to assess whether the test Band-Aids produced fewer complaints than the regular Band-Aids, you need to assess the association in sets of tables instead of the association in a single table.

Extended Mantel-Haenszel statistics, also known as Cochran-Mantel-Haenszel statistics, provide a way of assessing association between two variables that determine a table while controlling for, or adjusting for, the variables that determine the sets of tables. These variables are also known as stratification variables. In this instance, the statistics can provide a way to assess the association between Band-Aid type and complaint status while controlling for clinic.

In the first section, the odds ratio was presented as a measure of association. You can also compute an overall odds ratio for a set of tables that has been adjusted for the stratification variables.

The Studybandaid data set contains the information collected in this clinical trial and includes data that constitute tables for each of the five clinics.

Open the Studybandaid Data Set

These data are provided as the Studybandaid data set in the Analyst Sample Library. To open the Studybandaid data set, follow these steps:

Select Tools Sample Data ...
Select Studybandaid.
Click OK to create the sample data set in your Sasuser directory.
Select File Open By SAS Name ...
Select Sasuser from the list of Libraries.
Select Studybandaid from the list of members.
Click OK to bring the Studybandaid data set into the data table.

Figure 9.15 displays the data table containing these data. Note that the data are in frequency form, with the variable count containing the frequencies of the profile contained in each row of the table. The column corresponding to the variable clinic contains the values for the five clinics.

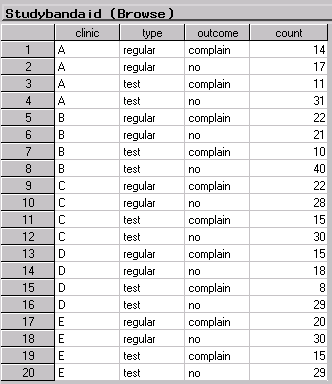Figure 9.15: Data Set Studybandaid in the Data Table

Specify the Tables

To request individual table tests of association as well as the CMH tests for the association of type of Band-Aid with complaint outcome, first specify the tables under study.

Select Statistics Table Analysis ...
Select type from the candidate list as the Row variable.
Select outcome from the candidate list as the Column variable.
Select clinic from the candidate list as the Strata variable.
Select count from the candidate list as the Cell Counts variable.

Figure 9.16 displays the resulting dialog.

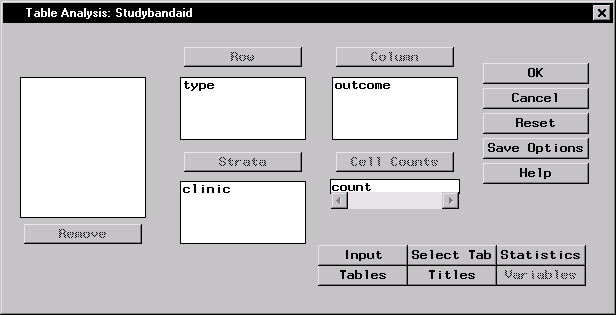Figure 9.16: Table Analysis Task for Band-Aid Study

Request Tests and Measures of Association

Use the Statistics dialog to specify the tests.

Click on the Statistics button.
Select Chi-square statistics.
Select Mantel-Haenszel Statistics.
Click OK.

Note that the Tables dialog specifications (see Figure 9.5) made previously remain in effect. Therefore, both frequencies and row percentages are produced for this analysis.

Click OK in the Table Analysis dialog to perform the analysis.

Review the Results

The results produced include individual tables, individual table statistics, and the summary chi-square statistics.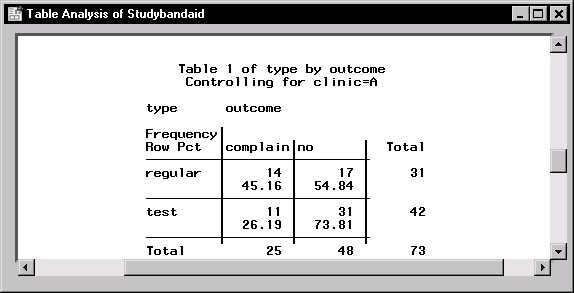

Figure 9.17: Frequency Table for Clinic A

Figure 9.17 contains the frequency table for clinic A.

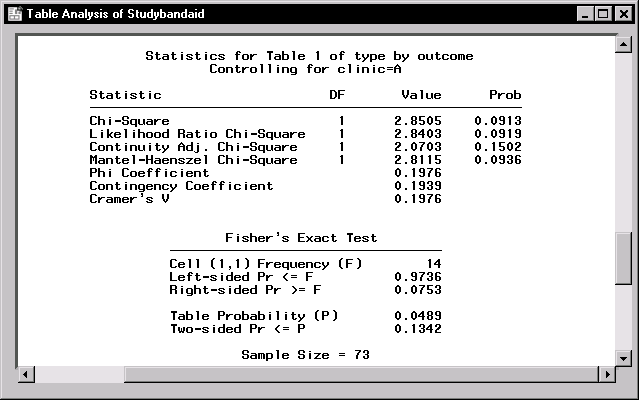Figure 9.18: Table Statistics for Clinic A

Figure 9.18 contains the table statistics for clinic A. The Pearson chi-square statistic has the value 2.8505 and a p-value of 0.091 with 1 degree of freedom.

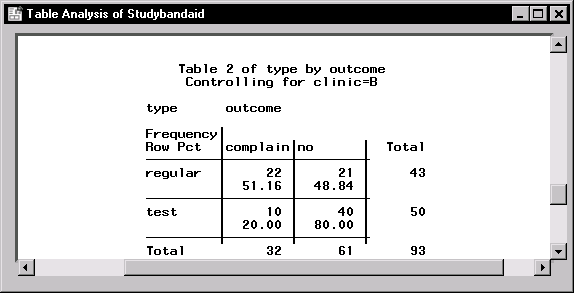Figure 9.19: Frequency Table for Clinic B

Figure 9.19 contains the frequency table for clinic B.

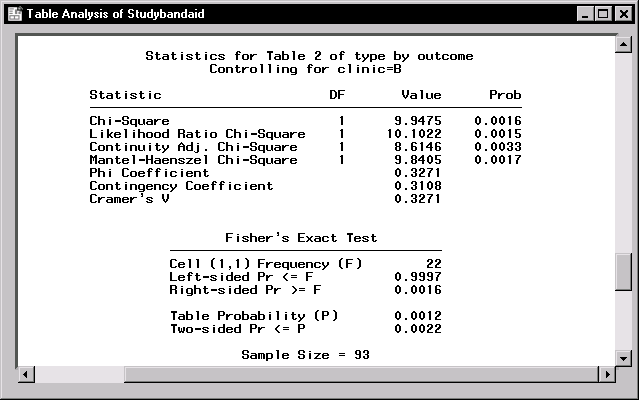Figure 9.20: Table Statistics for Clinic B

Figure 9.20 contains the associated table statistics. The Pearson chi-square statistic has a value of 9.9475 and a corresponding p-value of 0.0016.

The other individual tables, not printed here, show varying degrees of evidence of association. Clinic C and clinic E appear to have no evidence of association, while clinic D does appear to show evidence of association.

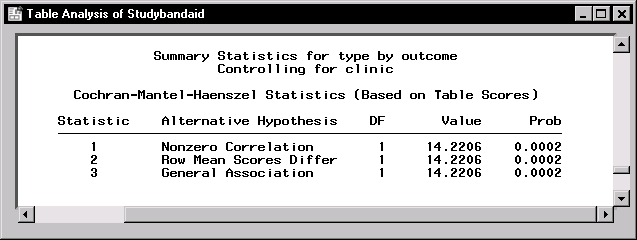Figure 9.21: CMH Summary Table

Figure 9.21 displays the results of the CMH analysis. Three versions of the CMH statistic are printed; all have the value 14.2206 and a p-value of 0.0002 with 1 degree of freedom. Your choice of statistic depends on the scale of variables that determine the rows and columns. The General Association statistic always applies. If the columns can be considered ordered, or ordinal, then the Row Mean Score statistic is appropriate as well and is directed at location shifts. If both the columns and rows are ordered, then the Correlation statistic is also appropriate and is directed at linear association. The degrees of freedom of these statistics vary. For more details, refer to Stokes, Davis, and Koch (1995). Note that the sample size requirement for the CMH statistics is that the total (tables combined) sample size be adequate.

In the case of the 2 ×2 table, all of these statistics are equivalent. Here, you can conclude that type of Band-Aid is significantly associated with complaint status, controlling for clinic. Figure 9.22 displays the overall relative risk and odds ratios and their confidence bounds.

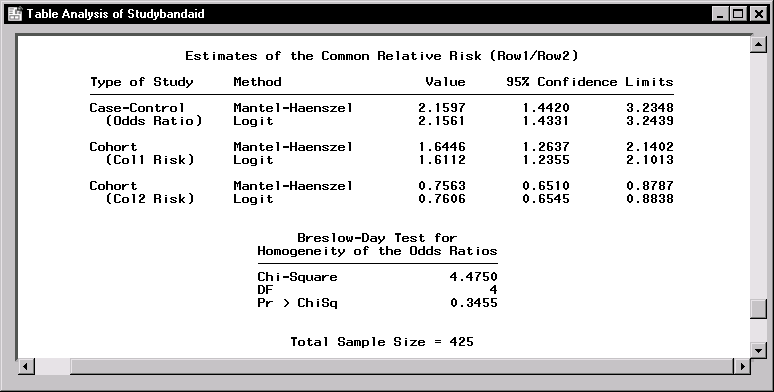Figure 9.22: Odds Ratio

The odds ratio for this study has the value 2.1597 with a confidence bound of (1.4420, 3.2348). This means that those children with the regular Band-Aid are twice as likely to have complaints as those with the test Band-Aid or, conversely, that those children with the test Band-Aid are half as likely to have complaints as those children with the regular Band-Aid. Since the 95 percent confidence bounds don't include the value 1, this odds ratio is considered to be significantly different from 1.

Note that another test called the Breslow-Day test for Homogeneity of Odds Ratio is also printed. Since the test has a p-value of 0.3455, you would conclude that the hypothesis is not rejected. The sample size requirement for this test is that each individual table has to have sufficient sample size unlike the sample size requirement for the CMH statistics. In this case, since all tables have totals greater than 25, this condition is met.

Top of Page