Usage Note 69066: The effect of time in repeated measures analysis in the MIXED procedure
 |  |  |
When you have repeated measures data and the response variable is assumed normal, you typically use PROC MIXED to analyze the data. One of the possible models is to use the REPEATED statement in PROC MIXED to model the correlations in your data. However, with different data situations for your TIME variable, and different model specifications in your PROC MIXED program, the results might not be what you expect, as explained below for three scenarios.
The repeated measures data comes from the example titled "Repeated Measures" in the PROC MIXED documentation. The name of the time variable is changed from Age to Time for clarity.
data pr;
input Person Gender $ y1 y2 y3 y4;
y=y1; Time=8; output;
y=y2; Time=10; output;
y=y3; Time=12; output;
y=y4; Time=14; output;
drop y1-y4;
datalines;
1 F 21.0 20.0 21.5 23.0
2 F 21.0 21.5 24.0 25.5
3 F 20.5 24.0 24.5 26.0
4 F 23.5 24.5 25.0 26.5
5 F 21.5 23.0 22.5 23.5
6 F 20.0 21.0 21.0 22.5
7 F 21.5 22.5 23.0 25.0
8 F 23.0 23.0 23.5 24.0
9 F 20.0 21.0 22.0 21.5
10 F 16.5 19.0 19.0 19.5
11 F 24.5 25.0 28.0 28.0
12 M 26.0 25.0 29.0 31.0
13 M 21.5 22.5 23.0 26.5
14 M 23.0 22.5 24.0 27.5
15 M 25.5 27.5 26.5 27.0
16 M 20.0 23.5 22.5 26.0
17 M 24.5 25.5 27.0 28.5
18 M 22.0 22.0 24.5 26.5
19 M 24.0 21.5 24.5 25.5
20 M 23.0 20.5 31.0 26.0
21 M 27.5 28.0 31.0 31.5
22 M 23.0 23.0 23.5 25.0
23 M 21.5 23.5 24.0 28.0
24 M 17.0 24.5 26.0 29.5
25 M 22.5 25.5 25.5 26.0
26 M 23.0 24.5 26.0 30.0
27 M 22.0 21.5 23.5 25.0
;
The following statements fit the model to be used throughout.
proc mixed data=pr ;
class Person Gender Time;
model y = Gender Time Gender*Time / s;
repeated Time / type=ar(1) subject=Person r;
run;
Following is partial output.
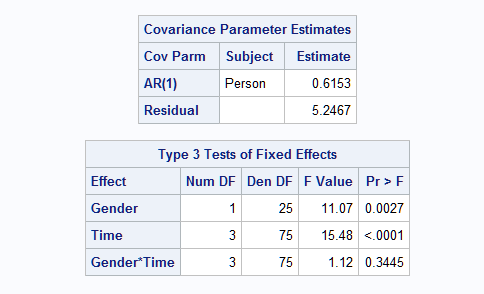 |
1. Missing Values for Some Time Points
The PR data set is balanced in that each subject has four repeated measures at time values of 8, 9, 10, and 11. Now suppose that not every subject has all four repeated measures, as in data set NEW, and the model is refitted.
data new;
set pr;
if _n_ in (4,5,6,15,16,26) then delete;
run;
proc mixed data=new ;
class Person Gender Time;
model y = Gender Time Gender*Time / s;
repeated Time / type=ar(1) subject=Person r;
run;
Partial results that reflect the change in the data are shown below:
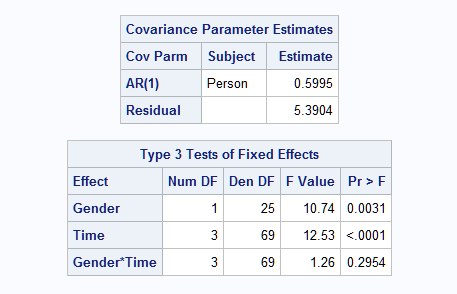 |
However, if you do not specify the repeated effect, TIME, in the REPEATED statement, you get different and incorrect results that might be unexpected.
proc mixed data=new ;
class Person Gender Time;
model y = Gender Time Gender*Time / s;
repeated / type=ar(1) subject=Person r;
run;
Here are the results from this analysis.
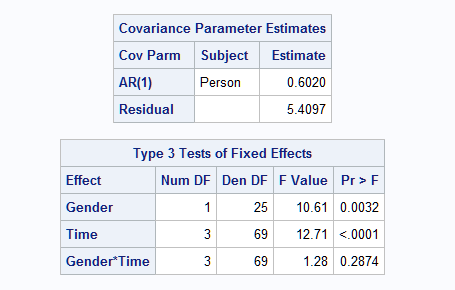 |
The reason the two approaches produce different results is that without the TIME effect in the REPEATED statement, the repeated measures for subjects are treated differently. To explain this problem, examine the first few observations in data set NEW.
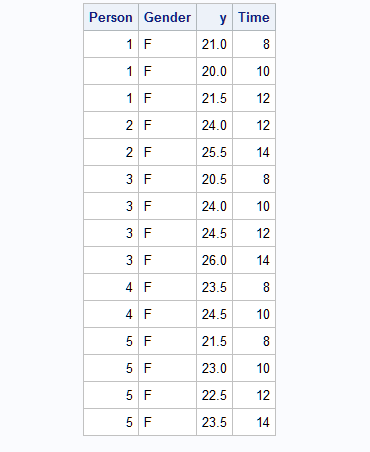 |
For subject 2, the repeated measures are considered the second and fourth time points for the model when the repeated effect, TIME, is in the REPEATED statement. However, they are considered the first and second time points when TIME is not specified as the repeated effect in the REPEATED statement. Therefore, it is recommended that you specify the repeated effect whenever possible in the REPEATED statement in PROC MIXED.
2. Specifying the REF= Option for TIME in the CLASS Statement
You can specify the REF= option in the CLASS statement so that the "Solutions for Fixed Effects" table produces the differences with the desired reference level. However, this option can cause the repeated measures to be sorted in a different order and therefore produce unexpected results. That is illustrated below.
proc mixed data=pr ;
class Person Gender Time(ref='8');
model y = Gender Time Gender*Time / s;
repeated Time / type=ar(1) subject=Person r;
run;
Partial output follows.
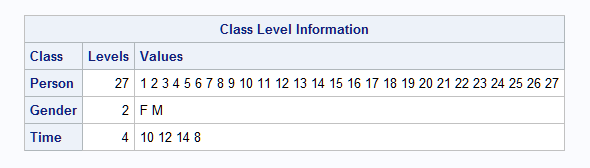 |
Note that in PROC MIXED (also in the GLM and GLIMMIX procedures), specifying the reference category essentially reorders the levels for the CLASS variable. In this case, the order for TIME is 10 12 14 8. So the observation for time 8 is considered the last time point and that affects the estimation of the AR(1) parameters. The results are also affected as shown below.
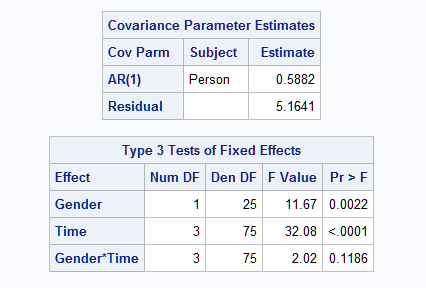 |
It is recommended that you do not use the REF= option to change the order of the levels of the TIME variable unless the change creates the proper chronological order.
If you want to compare the mean response at different time points against a certain time point, you can use the LSMEANS statement with the DIFF=CONTROL option to specify the desired reference time level.
lsmeans time / diff=control('8');
If you need to use TIME='8' as the reference level but still preserve the natural order of time for the AR(1) covariance structure, you can create a duplicate TIME variable, such as TIME1, and use TIME1 as the REPEATED effect. Here is an example:
data pr;
set pr;
Time1=Time;
run;
proc mixed data=pr ;
class Person Gender Time(ref='8') Time1;
model y = Gender Time Gender*Time / s;
repeated Time1 / type=ar(1) subject=Person r;
run;
3. Appending New Observations to Obtain Predicted Values for Them
The following approach is often used to obtain predicted values for a data set of new observations. This approach works with many modeling procedures.
- Create a scoring data set with values for all independent variables in your model and the values for which you want to obtain predicted values. The values for the response variable are all set to missing.
- Append this scoring data set to the original data set.
- Run your model using this combined data set and use the appropriate statement or option to obtain predicted values. In PROC MIXED, use the OUTP= option in the MODEL statement to obtain a data set of predicted values.
Because the observations in the scoring data set have missing values for the response variable, they are not used in the model estimation process. The model results should be unaffected and, by including these observations in the data set, predicted values are computed for these observations. However, the model fit might not be unaffected.
Suppose the following is your scoring data set.
data scoring;
input person gender $ time y;
datalines;
1 F 8.5 .
13 M 9.5 .
30 F 10 .
;
After combining the original data and this scoring data set, you can refit the model.
data all;
set pr scoring;
run;
proc mixed data=all ;
class Person Gender Time;
model y = Gender Time Gender*Time / s outp=preddata;
repeated Time / type=ar(1) subject=Person r;
run;
Following is partial output. Note that the TIME values in the original data set, 8, 10, 12, and 14, are considered now the first, fourth, fifth, and sixth time points and therefore the results are affected, as shown below.
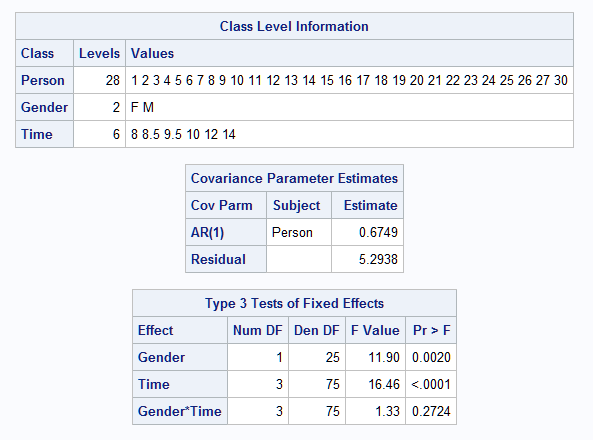 |
The resulting predicted values for the new observations in the scoring data set are based on a different set of parameter estimates than the original ones.
Another scoring approach is to use the STORE statement in PROC MIXED to save the fitted model, and then use the SCORE statement in the PLM procedure to obtain the predicted values as shown below.
proc mixed data=pr ;
class Person Gender Time;
model y = Gender Time Gender*Time / s ;
repeated Time / type=ar(1) subject=Person r;
store mxout;
run;
proc plm restore=mxout;
score data=scoring out=preddata2 predicted=pred;
run;
Here are some things to be aware of with this approach:
- The predicted vales from PROC PLM will not be kriging predictions as is the case in the OUTP= data set with PROC MIXED. Instead, they will be the same predicted values as reported by the PROC GLIMMIX model with only a random R-side effect. If you want the kriging predictions, then do not use PROC PLM.
- When you specify a RANDOM statement in PROC MIXED, the SCORE statement in PROC PLM does not compute the predicated values involving random effects. If you want the predicted values to include the random effects, consider using the LMIXED procedure with the STORE statement in SAS® Viya® to fit your mixed model. Then use the ASTORE procedure with the SCORE statement to obtain predicted values.
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | z/OS | ||
| z/OS 64-bit | ||||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 8.1 Pro x64 | ||||
| Microsoft Windows 10 | ||||
| Microsoft Windows 11 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows Server 2016 | ||||
| Microsoft Windows Server 2019 | ||||
| Microsoft Windows Server 2022 | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | Analytics ==> Mixed Models Analytics ==> Regression Analytics ==> Scoring SAS Reference ==> Procedures ==> GLIMMIX SAS Reference ==> Procedures ==> MIXED |
| Date Modified: | 2025-10-21 15:42:24 |
| Date Created: | 2022-04-07 15:30:20 |