Usage Note 57738: Solving the shortest path problem with the OPTMODEL and OPTNET procedures
 |  |  |
The shortest path problem finds the path between nodes in a graph such that the sum of the weights (such as costs) is minimized. Some examples of shortest path problems include driving directions, network routing, operating schedules, and social networking. PROC OPTMODEL can be used to find the shortest path in a graph. Beginning in SAS® 9.3 TS1M2, PROC OPTNET can also be used. Both procedures are part of SAS/OR® software.
The following network flow example is presented in Ahuja et. al. (1993). The diagram shows the costs for traversing between nodes of the network. The goal is to move from node 1 to node 6 with minimum cost.
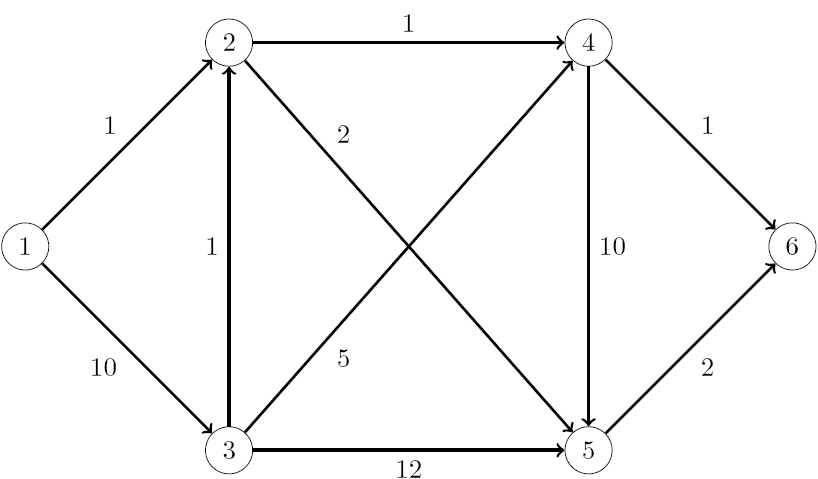
|
The network is summarized in the following data. Variables i and j represent the flow from node i to node j with the associated cost and time.
data arc_data;
input i j cost time;
datalines;
1 2 1 10
1 3 10 3
2 4 1 1
2 5 2 3
3 2 1 2
3 4 5 7
3 5 12 3
4 5 10 1
4 6 1 7
5 6 2 2
;
The destination of the graph starts at the source node and ends at the sink node.
%let source = 1;
%let sink = 6;
Three ways of solving this problem are shown. First, the LP solver is used in PROC OPTMODEL. The network solver in PROC OPTMODEL can also solve the problem and is shown next. Finally, PROC OPTNET is used.
LP Solver in PROC OPTMODELThe following PROC OPTMODEL statements solve this shortest path problem. The sum of the costs of the arcs is the objective function to be minimized. Starting from the source node (node 1), the solution is subject to the constraint that only one path may be taken to the sink node (node 6).
proc optmodel;
/* Declare sets and parameters, and read data */
set <num,num> ARCS;
num cost {ARCS};
read data arc_data into ARCS=[i j] cost;
put (card(ARCS))=;
print cost;
set NODES = union {<i,j> in ARCS} {i,j};
put (card(NODES))=;
num source = &source;
num sink = &sink;
/* Declare decision variables */
var Flow {ARCS} >= 0;
/* Declare objective */
min TotalCost =
sum {<i,j> in ARCS} cost[i,j] * Flow[i,j];
/* Declare constraints */
con Balance {i in NODES}:
sum {<(i),j> in ARCS} Flow[i,j]
- sum {<j,(i)> in ARCS} Flow[j,i]
= (if i = source then 1 else if i = sink then -1 else 0);
/* Display algebraic expansion of model */
expand;
/* Call LP solver */
solve;
/* Save Solution */
create data solution_data1 from [i j] Flow;
/* Save Solution (Sparse Form) */
create data solution_data2 from [i j]={<i,j> in ARCS: Flow[i,j].sol > 1e-6} Flow cost;
quit;
The "Objective Value" in the Solution Summary table shows that the minimum cost for the shortest path in this network is 3.
| ||||||||||||||||||||||||||||
The CREATE DATA statements save the solution in two different forms which are displayed by the following statements.
proc print data=solution_data1;
id i j;
title 'Arc Flow Decision Variables At The Solution';
run;
proc print data=solution_data2;
id i j;
title 'Arc Flows Used At Optimal Solution';
run;
The "Arc Flow Decision Variables At The Solution" table shows each possible flow from one node to another (the decision variables of the problem) and the value of the decision variable at the solution. If the value of the decision variable is 1, it is used in the solution for the shortest path. If the value is 0, it is not used in the solution. The "Arc Flows Used At Optimal Solution" table shows only the decision variables that are used in the solution and their associated cost. This form is particularly useful if the network is large and you want to print only the decision variables greater than zero that are in the solution.
|
The optimal solution found by PROC OPTMODEL can be represented in the following network diagram. It shows that the optimal flow for the shortest path is to go from node 1 to node 2 with a cost of 1, from node 2 to node 4 with a cost of 1, and node 4 to node 6 with a cost of 1.
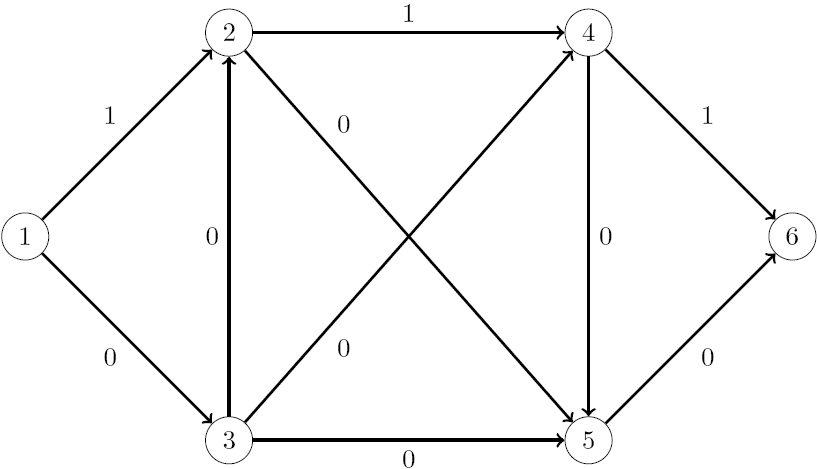
|
The network solver in PROC OPTMODEL can also solve the shortest path problem by using the SHORTPATH= option in the SOLVE WITH NETWORK statement. Using the SOURCE= and SINK= suboptions, PROC OPTMODEL calculates the shortest path between one source and one sink node. These statements solve the problem and display the solution.
proc optmodel;
/* Declare sets and parameters, and read data */
set <num,num> LINKS;
num cost{LINKS};
read data arc_data into LINKS=[i j] cost;
set <num,num,num,num,num> PATHS; /* source, sink, order, from, to */
set <num,num> PATH_EDGES = setof {<o,d,order,i,j> in PATHS} <i,j>;
set SOURCES = {&source};
set SINKS = {&sink};
/* Call the network solver using the shortest path algorithm */
solve with network /
graph_direction = directed
links = (weight=cost)
shortpath = (source=SOURCES sink=SINKS)
out = (sppaths=PATHS)
;
put PATHS;
put PATH_EDGES;
/* Save solution */
create data ShortPath from [source sink order i j]=PATHS cost[i,j];
quit;
proc print data=shortpath;
id order;
var i j cost;
title 'Shortest Path for One Source-Sink Pair';
run;
The "Shortest Path for One Source-Sink Pair" table shows the shortest path.
|
The problem can also be solved using PROC OPTNET. These statements read the network data and use the shortest path algorithm to find the optimal solution and save it in a data set.
proc optnet
data_links = arc_data
/* Specify a directed graph */
graph_direction = directed;
/* Specify the flow of the network */
data_links_var
from = i
to = j
weight = cost;
/* Invoke shortest path algorithm */
shortpath
source = &source
sink = &sink
/* Save solution to solution_data data set */
out = solution_data;
run;
These statements display the optimal solution.
proc print data=solution_data;
id order;
var i j cost;
sum cost;
run;
Note that the same solution is found with total cost of 3.
|
Reference
Ahuja, R. K., Magnanti, T. L., and Orlin, J. B. (1993). Network Flows: Theory, Algorithms, and Applications. Englewood Cliffs, NJ: Prentice-Hall.Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/OR | z/OS | ||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Pro | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 10 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | SAS Reference ==> Procedures ==> OPTMODEL Analytics ==> Mathematical Optimization SAS Reference ==> Procedures ==> OPTNET |
| Date Modified: | 2016-08-09 16:55:06 |
| Date Created: | 2016-02-26 10:54:17 |