Sample 45612: Bayesian Multinomial Model for Ordinal Data Using SAS/STAT 9.2
 |  |  |  |
Analysis
Researchers study the results of a taste test on three different brands of ice cream. They want to assess the testers’ preference of the three brands. The taste of each brand is rated on a five-point scale from very good to very bad. the five points correspond to response variables Y1 through Y5, where Y1 represents very good and Y5 represents very bad. Response variables contain the number of taste testers who rate each brand in each category. The very bad taste level (Y5) is used as the reference response level. Two dummy variables, BRAND1 and BRAND2, are created to indicate Brands 1 and 2, respectively. Brand 3 is set as the reference level in this example and is represented in the data set when both of the dummy variables equal zero.
The following statements create the ICECREAM data set:
data icecream;
input y1-y5 brand;
if brand = 1 then brand1 = 1;
else brand1 = 0;
if brand = 2 then brand2 = 1;
else brand2 = 0;
keep y1-y5 brand1 brand2;
datalines;
70 71 151 30 46 1
20 36 130 74 70 2
50 55 140 52 50 3
;
Bayesian Multinomial Model
Multinomial ordinal models occur frequently in applications such as food testing, survey response, or anywhere order matters in the categorical response. Categorical data with an ordinal response correspond to multinomial models based on cumulative response probabilities (. In this data set, the ordered response variable is the taste tester’s rating for a brand of ice cream.
Let the random variable
 for brand
for brand
 , and let response level
, and let response level
 , be from an multinomial ordinal model with mutually exclusive,
discrete response levels and probability mass function
, be from an multinomial ordinal model with mutually exclusive,
discrete response levels and probability mass function

|
where 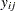 represents the number of people from
represents the number of people from 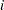 th brand in the
th brand in the  th response level. For the grouped data, let
th response level. For the grouped data, let  denote the number of testers who taste the
denote the number of testers who taste the 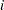 th brand of ice cream and let
th brand of ice cream and let  . Let
. Let  denote the probability that the response of brand
denote the probability that the response of brand 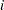 falls into the
falls into the  th response level, and let
th response level, and let 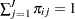 . Let
. Let 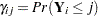 denote the corresponding cumulative probability that the response falls in the
denote the corresponding cumulative probability that the response falls in the  th level or below, so
th level or below, so  . The transformed cumulative probabilities are linear functions of the covariates written as
. The transformed cumulative probabilities are linear functions of the covariates written as 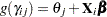 , where
, where  refers to the logit link function,
refers to the logit link function,  represents the effects for the covariates, and
represents the effects for the covariates, and  . Let
. Let  represent the baseline value of the transformed cumulative probability for category
represent the baseline value of the transformed cumulative probability for category  such that the constraint
such that the constraint 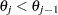 holds for all
holds for all  (. Then
(. Then
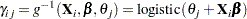
|
(1) |
and the group probabilities for the  th levels are as follows:
th levels are as follows:

|
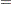
|

|
(2) | ||

|
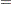
|

|
|||

|
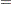
|

|
(3) | ||

|
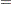
|

|
|||

|
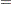
|
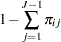
|
(4) |
The likelihood function for the counts and corresponding covariates is
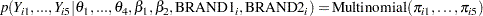
|
(5) |
where  denotes a conditional probability density. The multinomial density is evaluated at the specified value of
denotes a conditional probability density. The multinomial density is evaluated at the specified value of 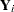 and the corresponding probabilities
and the corresponding probabilities 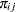 , which are defined in Equation 2 through 4.
, which are defined in Equation 2 through 4.
There are six parameters in the likelihood: the intercepts 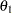 through
through  and the regression parameters
and the regression parameters 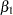 and
and  that correspond to the relative Brand 1 and 2 effects, respectively.
that correspond to the relative Brand 1 and 2 effects, respectively.
Suppose the following prior distributions are placed on the six parameters, where  indicates a prior distribution and
indicates a prior distribution and  indicates a conditional prior distribution:
indicates a conditional prior distribution:

|
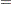
|

|
(6) | ||
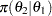
|
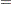
|

|
(7) | ||

|
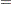
|

|
(8) | ||
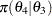
|
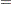
|

|
(9) | ||

|
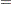
|

|
(10) |
The joint prior distribution of 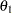 through
through  is the product of Equation 6 through 9. The prior distributions in Equation 7 through 9 represent truncated normal distributions with mean 0, variance 100, and the designated lower bound. The lower bound ensures that the order restriction on
is the product of Equation 6 through 9. The prior distributions in Equation 7 through 9 represent truncated normal distributions with mean 0, variance 100, and the designated lower bound. The lower bound ensures that the order restriction on  is sustained.
is sustained.
Using Bayes’ theorem, the likelihood function and prior distributions determine the posterior distribution of the parameters as follows:

|

|

|
|||

|
PROC MCMC obtains samples from the desired posterior distribution. You do not need to specify the exact form of the posterior distribution.
The odds ratio for comparing one brand to another can be written as

|
(11) |
for
 . The odds ratio is useful for interpreting how the taste
preference for the different brands of ice cream cpmpares. For this example, Brand 3 is set as the reference level, which implies that
. The odds ratio is useful for interpreting how the taste
preference for the different brands of ice cream cpmpares. For this example, Brand 3 is set as the reference level, which implies that
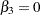 .
.
The following SAS statements fit the Bayesian multinomial ordinal model. The PROC MCMC statement invokes the procedure and specifies the input data set. The NBI= option specifies the number of burn-in iterations. The NMC= option specifies the number of posterior simulation iterations. The THIN=10 option specifies that one of every 10 samples is kept. The SEED= option specifies a seed for the random number generator (the seed guarantees the reproducibility of the random stream). The PROPCOV=QUANEW option uses the estimated inverse Hessian matrix as the initial proposal covariance matrix. The MONITOR= option outputs analysis on selected symbols of interest in the program.
ods graphics on;
proc mcmc data=icecream nbi=10000 nmc=25000 thin=10 seed=1181
propcov=quanew monitor=(beta1 beta2 or12 or13 or23);
array theta[4];
array gamma[4];
parms theta1-theta4 beta1 beta2;
prior beta: ~ normal(0,var=1000);
prior theta1 ~ normal(0,var=100);
prior theta2 ~ normal(0,var=100,lower=theta1);
prior theta3 ~ normal(0,var=100,lower=theta2);
prior theta4 ~ normal(0,var=100,lower=theta3);
mu = beta1*brand1 + beta2*brand2;
do j = 1 to 4;
gamma[j] = logistic(theta[j] + mu);
end;
pi1 = gamma1;
pi2 = gamma2 - gamma1;
pi3 = gamma3 - gamma2;
pi4 = gamma4 - gamma3;
pi5 = 1 - sum(of pi1-pi4);
llike = logmpdfmultinom(of y1-y5, of pi1-pi5);
model dgeneral(llike);
beginnodata;;
or12 = exp(beta1-beta2);
or13 = exp(beta1);
or23 = exp(beta2);
endnodata;;
run;
ods graphics off;
Each of the two ARRAY statements associates a name with a list of variables and constants. The first ARRAY statement specifies names for the intercept parameters. The second ARRAY statement contains the  parameters.
parameters.
The PARMS statement puts all six parameters in a single block. The PRIOR statements specify priors for the parameters as given in Equations 6 through 10.
The MU assignment statement calculates  . The DO loop and coinciding GAMMA assignment statements calculate
. The DO loop and coinciding GAMMA assignment statements calculate  for
for  as in Equation 1. The five ETA assignment statements calculate the individual probabilities that an observation falls into the
as in Equation 1. The five ETA assignment statements calculate the individual probabilities that an observation falls into the  th response level as in Equation 2 to Equation 4.
th response level as in Equation 2 to Equation 4.
The LLIKE statement uses the multivariate LOGMPDFMULTIM function to calculate the value of the log likelihood function as in Equation 5. The multinomial density is not listed in the section "Standard Distributions" in the PROC MCMC documentation, so you use the DGENERAL function in the MODEL statement. The letter "D" stands for discrete. The log likelihood is the input parameter because the DGENERAL function must be specified on the logarithm scale. Since the multivariate log likelihood function takes the dependent variable into account, you do not need to explicitly state the dependent variable in the MODEL statement.
The statements within the BEGINNODATA and ENDNODATA statements calculate the three odds ratios for pairwise comparisons of ice cream brands according to Equation 11. The statements are enclosed within the BEGINNODATA and ENDNODATA block to reduce unnecessary observation-level computations.
Figure 1 displays diagnostic plots to assess whether the Markov chains have converged.

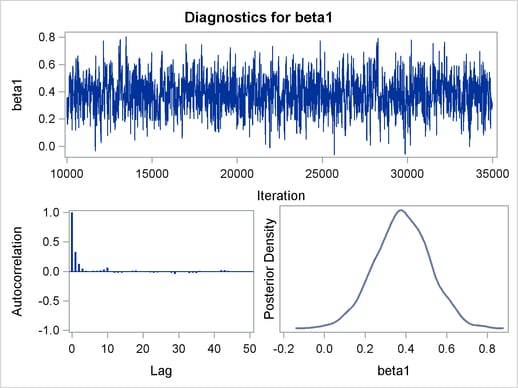
The trace plot in Figure 1 indicates that the chain appears to have reached a stationary distribution. It also has good mixing and is dense.
The autocorrelation plot indicates low autocorrelation and efficient sampling. Finally, the kernel density plot shows the smooth, unimodal shape of posterior marginal distribution for
 . The remaining diagnostic plots (not shown here) similarly indicate good
convergence in the other parameters.
. The remaining diagnostic plots (not shown here) similarly indicate good
convergence in the other parameters.
Figure 2 displays a number of convergence diagnostics, including Monte Carlo standard errors, autocorrelations at selected lags, Geweke diagnostics, and the effective sample sizes.
| Monte Carlo Standard Errors | |||
|---|---|---|---|
| Parameter | MCSE | Standard Deviation |
MCSE/SD |
| beta1 | 0.00379 | 0.1337 | 0.0283 |
| beta2 | 0.00449 | 0.1403 | 0.0320 |
| or12 | 0.0119 | 0.4054 | 0.0294 |
| or13 | 0.00562 | 0.1981 | 0.0284 |
| or23 | 0.00236 | 0.0743 | 0.0317 |
| Posterior Autocorrelations | ||||
|---|---|---|---|---|
| Parameter | Lag 1 | Lag 5 | Lag 10 | Lag 50 |
| beta1 | 0.3284 | -0.0011 | 0.0618 | -0.0120 |
| beta2 | 0.4089 | 0.0287 | 0.0232 | 0.0142 |
| or12 | 0.3465 | 0.0059 | 0.0297 | -0.0029 |
| or13 | 0.3260 | 0.0014 | 0.0607 | -0.0130 |
| or23 | 0.3967 | 0.0338 | 0.0266 | 0.0144 |
| Geweke Diagnostics | ||
|---|---|---|
| Parameter | z | Pr > |z| |
| beta1 | -0.1114 | 0.9113 |
| beta2 | -1.5302 | 0.1260 |
| or12 | 1.4711 | 0.1413 |
| or13 | -0.1486 | 0.8819 |
| or23 | -1.5676 | 0.1170 |
| Effective Sample Sizes | |||
|---|---|---|---|
| Parameter | ESS | Autocorrelation Time |
Efficiency |
| beta1 | 1246.3 | 2.0060 | 0.4985 |
| beta2 | 978.1 | 2.5560 | 0.3912 |
| or12 | 1157.6 | 2.1596 | 0.4631 |
| or13 | 1243.9 | 2.0098 | 0.4976 |
| or23 | 992.7 | 2.5184 | 0.3971 |
Figure 3 reports summary and interval statistics for the regression parameters and odds ratios. The odds ratios provide the relative difference
in one brand with respect to another and indicate whether there is a significant brand effect. The odds ratio for Brand 1 and Brand 2 is the multiplicative change in the odds of a
taste tester preferring Brand 1 compared to the odds of the tester preferring Brand 2. The estimated odds ratio
( ) value is 2.8366 with a corresponding 95% equal-tail
credible interval of
) value is 2.8366 with a corresponding 95% equal-tail
credible interval of  . Similarly, the odds ratio for
Brand 1 and Brand 3 is 1.4787 with a 95% equal-tail credible interval of
. Similarly, the odds ratio for
Brand 1 and Brand 3 is 1.4787 with a 95% equal-tail credible interval of
 . Finally, the odds ratio for Brand 2 compared to Brand
3 is 0.5271 with a 95% equal-tail credible interval of
. Finally, the odds ratio for Brand 2 compared to Brand
3 is 0.5271 with a 95% equal-tail credible interval of  .
The lower categories indicate the favorable taste results; so Brand 1 scored significantly better when compared to Brand 2 or 3. Brand 2 scored less favorably when compared to Brand 3.
.
The lower categories indicate the favorable taste results; so Brand 1 scored significantly better when compared to Brand 2 or 3. Brand 2 scored less favorably when compared to Brand 3.
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| beta1 | 2500 | 0.3822 | 0.1337 | 0.2957 | 0.3810 | 0.4718 |
| beta2 | 2500 | -0.6502 | 0.1403 | -0.7456 | -0.6488 | -0.5590 |
| or12 | 2500 | 2.8366 | 0.4054 | 2.5518 | 2.8079 | 3.1088 |
| or13 | 2500 | 1.4787 | 0.1981 | 1.3440 | 1.4638 | 1.6029 |
| or23 | 2500 | 0.5271 | 0.0743 | 0.4745 | 0.5227 | 0.5718 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| beta1 | 0.050 | 0.1135 | 0.6443 | 0.1081 | 0.6344 |
| beta2 | 0.050 | -0.9297 | -0.3736 | -0.9357 | -0.3828 |
| or12 | 0.050 | 2.1197 | 3.6740 | 2.0851 | 3.6103 |
| or13 | 0.050 | 1.1202 | 1.9046 | 1.1059 | 1.8741 |
| or23 | 0.050 | 0.3947 | 0.6882 | 0.3849 | 0.6714 |
References
-
Albert, J. H. and Chib, S. (1993), “Bayesian Analysis of Binary and Polychotomous Response Data,” Journal of the American Statistical Association, 88(422), 669–679.
-
McCullagh, P. and Nelder, J. A. (1989), Generalized Linear Models, Second Edition, London: Chapman & Hall.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
data icecream;
input y1-y5 brand;
if brand = 1 then brand1 = 1;
else brand1 = 0;
if brand = 2 then brand2 = 1;
else brand2 = 0;
keep y1-y5 brand1 brand2;
datalines;
70 71 151 30 46 1
20 36 130 74 70 2
50 55 140 52 50 3
;
ods graphics on;
proc mcmc data=icecream nbi=10000 nmc=25000 thin=10 seed=1181
propcov=quanew monitor=(beta1 beta2 or12 or13 or23);
array theta[4];
array gamma[4];
parms theta1-theta4 beta1 beta2;
prior beta: ~ normal(0,var=1000);
prior theta1 ~ normal(0,var=100);
prior theta2 ~ normal(0,var=100,lower=theta1);
prior theta3 ~ normal(0,var=100,lower=theta2);
prior theta4 ~ normal(0,var=100,lower=theta3);
mu = beta1*brand1 + beta2*brand2;
do j = 1 to 4;
gamma[j] = logistic(theta[j] + mu);
end;
pi1 = gamma1;
pi2 = gamma2 - gamma1;
pi3 = gamma3 - gamma2;
pi4 = gamma4 - gamma3;
pi5 = 1 - sum(of pi1-pi4);
llike = logmpdfmultinom(of y1-y5, of pi1-pi5);
model dgeneral(llike);
beginnodata;;
or12 = exp(beta1-beta2);
or13 = exp(beta1);
or23 = exp(beta2);
endnodata;;
run;
ods graphics off;
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
| Type: | Sample |
| Topic: | Analytics ==> Bayesian Analysis SAS Reference ==> Procedures ==> MCMC |
| Date Modified: | 2016-10-17 13:25:14 |
| Date Created: | 2012-02-08 15:42:21 |
Operating System and Release Information
| Product Family | Product | Host | Product Release | SAS Release | ||
| Starting | Ending | Starting | Ending | |||
| SAS System | SAS/STAT | z/OS | 9.22 | |||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | 9.22 | |||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | 9.22 | |||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | 9.22 | |||||
| Microsoft Windows XP 64-bit Edition | 9.22 | |||||
| Microsoft® Windows® for x64 | 9.22 | |||||
| Microsoft Windows 95/98 | 9.22 | |||||
| Microsoft Windows 2000 Advanced Server | 9.22 | |||||
| Microsoft Windows 2000 Datacenter Server | 9.22 | |||||
| Microsoft Windows 2000 Server | 9.22 | |||||
| Microsoft Windows 2000 Professional | 9.22 | |||||
| Microsoft Windows NT Workstation | 9.22 | |||||
| Microsoft Windows Server 2003 Datacenter Edition | 9.22 | |||||
| Microsoft Windows Server 2003 Enterprise Edition | 9.22 | |||||
| Microsoft Windows Server 2003 Standard Edition | 9.22 | |||||
| Microsoft Windows Server 2003 for x64 | 9.22 | |||||
| Microsoft Windows Server 2008 | 9.22 | |||||
| Microsoft Windows Server 2008 for x64 | 9.22 | |||||
| Microsoft Windows XP Professional | 9.22 | |||||
| Windows 7 Enterprise 32 bit | 9.22 | |||||
| Windows 7 Enterprise x64 | 9.22 | |||||
| Windows 7 Home Premium 32 bit | 9.22 | |||||
| Windows 7 Home Premium x64 | 9.22 | |||||
| Windows 7 Professional 32 bit | 9.22 | |||||
| Windows 7 Professional x64 | 9.22 | |||||
| Windows 7 Ultimate 32 bit | 9.22 | |||||
| Windows 7 Ultimate x64 | 9.22 | |||||
| Windows Millennium Edition (Me) | 9.22 | |||||
| Windows Vista | 9.22 | |||||
| Windows Vista for x64 | 9.22 | |||||
| 64-bit Enabled AIX | 9.22 | |||||
| 64-bit Enabled HP-UX | 9.22 | |||||
| 64-bit Enabled Solaris | 9.22 | |||||
| HP-UX IPF | 9.22 | |||||
| Linux | 9.22 | |||||
| Linux for x64 | 9.22 | |||||
| OpenVMS on HP Integrity | 9.22 | |||||
| Solaris for x64 | 9.22 | |||||