Sample 42514: Tests for comparing nested and nonnested models
 |  |  |  |  |
Tests for comparing nested and nonnested models
| Contents: | Purpose / History / Requirements / Usage / Details / Limitations / Missing Values / See Also / References |
- PURPOSE:
- Compare two nested or nonnested models fit by maximum likelihood. Nested models are compared using the likelihood ratio test. Nonnested models are compared using tests by Vuong or Clarke testing the hypothesis that both models are equally distant from the true model.
- HISTORY:
-
Version Update Notes 1.1 Added likelihood ratio test for nested models. Added FREQ= and WEIGHT= parameters for models fit to data containing frequencies and/or weights. 1.0 Initial version providing Vuong and Clarke tests for nonnested models. - REQUIREMENTS:
- Only Base SAS is required.
- USAGE:
- Follow the instructions in the Downloads tab of this sample to save the %VUONG macro definition. Before calling the %VUONG macro, specify the following %INC statement in your SAS program or in the SAS editor window to define the macro and make it available for use. In the %INC statement, replace the text within quotes with the location of the %VUONG macro definition file on your system.
%inc "<location of your file containing the VUONG macro>";
Following this statement, you can call the %VUONG macro using the following syntax. Macro arguments can be listed in any order.
%vuong(<list of macro arguments separated by commas>)
Before running the %VUONG macro, fit both models that you want to compare and save the predicted values from each. The DATA= data set analyzed by the macro must contain the common response variable used in both models and one variable from each model containing predicted or probability values. Also, if one or both models is a binomial model fit using events/trials syntax (that is, fit to aggregated or summarized data), then the variable containing the numbers of trials must be included. If one or both models is a zero-inflated Poisson (ZIP) or zero-inflated negative binomial (ZINB) model, then the variable containing zero-inflation probabilities must be included.
The easiest way to generate the necessary input data set is to use the output data set from fitting the first model as the input data set for fitting the second model. Then the output data set from fitting the second model should have all the necessary variables. The examples in the Results tab use this technique.
The following macro arguments are required:
- response=variable
- Specifies the common response variable in both models. Note that exactly the same response values must be used in estimating both models.
- p1=variable and p2=variable
- These parameters specify the variables containing the predicted values from the first and second model. These variables are created by the P= or PRED= option in the OUTPUT statement in the LOGISTIC, PROBIT, GENMOD, or COUNTREG procedure. In PROC MIXED (fixed effects models only), specify the OUTP= option in the MODEL statement. For models with nonnormal distributions fit in PROC GLIMMIX, use the PRED(ILINK)= option to produce this variable.
- dist1=NOR|BIN|MULT|GAM|IG|NB|POI|ZIP|ZINB|OTH and
dist2=NOR|BIN|MULT|GAM|IG|NB|POI|ZIP|ZINB|OTH - These parameters specify the distributions of the response in the first model and second model: NOR=normal, BIN=binomial, MULT=multinomial, GAM=gamma, IG=inverse Gaussian, NB=negative binomial, POI=Poisson, ZIP=zero-inflated Poisson, ZINB=zero-inflated negative binomial, OTH=other. Specify OTH if the corresponding predicted values variable (P1= or P2=) contains the observation likelihood contributions (rather than predicted values) from any distribution. For a normal, negative binomial, zero-inflated negative binomial, gamma, or inverse Gaussian model, the scale value must be specified in the corresponding scale parameter (SCALE1= or SCALE2=). For a zero-inflated Poisson or zero-inflated negative binomial model, specify the zero-inflation probability variable in the corresponding parameter (PZERO1= or PZERO2=).
The following macro arguments are optional except as noted.
- data=data-set-name
- Specifies the name of the input data set that contains the response variable and two variables holding the predicted values from each of the two models to be compared. If omitted the last created data set is used.
- model1=label
- Specifies a label (up to 40 characters) for the first model defined by the DIST1= and P1= parameters. The default label is Model 1.
- model2=label
- Specifies a label (up to 40 characters) for the second model defined by the DIST2= and P2= parameters. The default label is Model 2.
- test=BOTH|VUONG|CLARKE|LR
- Species whether to compute Vuong's test, Clarke's test, or both when comparing nonnested models or the likelihood ratio test when comparing nested models. The default is both.
- freq=variable
- Species the variable containing frequency counts if such a variable was used to fit the models.
- weight=variable
- Species the variable containing weights if such a variable was used to fit the models.
The NPARM1= and NPARM2= parameters must both be specified in order for the Akaike- and Schwarz-adjusted tests to be computed. If only one or neither is specified, then only the unadjusted tests are provided.
- nparm1=value
- Specifies the number of parameters estimated in the first model.
- nparm2=value
- Specifies the number of parameters estimated in the second model.
If a binomial model is being tested, one of the following two parameters must be specified. If events/trials syntax was used to fit the model to summarized data, specify the events variable in the RESPONSE= parameter and the trials variable in the TRIALS= parameter. If single variable syntax was used to fit the model to binary data, specify the response variable in the RESPONSE= parameter and specify the EVENT= parameter to indicate which response level is the event level.
- event=value | "value" | 'value'
- Specifies the value of the RESPONSE= variable that represents the event level that was modeled. If the RESPONSE= variable is a character variable, value must be enclosed in quotes.
- trials=variable
- Specifies a variable containing the number of trials in each observation. This is the trials variable used when fitting a binomial model with events/trials syntax in the MODEL statement. Specify the events variable in the RESPONSE= parameter.
One of the following parameters is required for each zero-inflated Poisson (ZIP) or zero-inflated negative binomial (ZINB) model being tested. This variable can be created by the PZERO= option in the OUTPUT statement of PROC GENMOD or the PROBZERO= option in the OUTPUT statement of PROC COUNTREG.
- pzero1=variable
- Specifies the variable containing the zero-inflation probabilities for the first model.
- pzero2=variable
- Specifies the variable containing the zero-inflation probabilities for the second model.
One of the following parameters is required for each normal, negative binomial, zero-inflated negative binomial, gamma, or inverse Gaussian model being tested.
- scale1=value
- Specifies the scale parameter value for the first model according to the table below.
- scale2=value
- Specifies the scale parameter value for the second model according to the table below.
Distribution GENMOD GLIMMIX* MIXED** COUNTREG Normal*** Scale √Scale √ Residual covariance
parameter estimateNegative
binomialDispersion Scale _Alpha ZINB Dispersion _Alpha Gamma Scale Scale Inverse
GaussianScale √Scale * Specify the NOREML option in the PROC GLIMMIX statement, the SOLUTION option in the MODEL statement, and the PRED(ILINK)= option in the OUTPUT statement.
** Fixed effects models only. Specify the METHOD=ML option in the PROC MIXED statement and the OUTP= option in the MODEL statement.
*** With PROC REG or PROC GLM, specify the Root MSE value in SCALE1= or SCALE2=.
The version of the %VUONG macro that you are using is displayed in the SAS log when you specify version (or any string) as the first argument. For example:
%vuong(version, ...other options...) - DETAILS:
- The %VUONG macro can compare nested models using the likelihood ratio test or nonnested models using the Vuong and/or Clarke tests.
Nested models
Two nested models fit using maximum likelihood (ML) can be compared using a likelihood ratio (LR) test statistic. The LR statistic is computed as twice the positive difference of the models' log likelihood values and is chi-square distributed with degrees of freedom equal to the positive difference in the number of model parameters. The LR test cannot be used to compare models that are nonnested, or models fit by methods other than maximum likelihood such as Generalized Estimating Equations (GEE). See also "Limitations on constructing valid LR tests" in Example 4 of this note.
Nonnested models
The %VUONG macro performs the Vuong and Clarke tests of the null hypothesis that both models are equally distant from the true model against a two-sided alternative hypothesis that one of the models is closer to the true model. If the test statistic is positive and significant, the null hypothesis is rejected in favor of the first model being closer to the true model. If the test statistic is negative and significant, the null hypothesis is rejected in favor of the second model being closer to the true model. A one-sided test, that one of the models is closer to the true model, can be performed by simply halving the p-value if the sign of the statistic is in the hypothesized direction.
Both tests are based on the Kullback-Leibler information criteria (KLIC). KLIC is a measure of "distance" between a model and the true model. Both tests assume the models being compared are strictly nonnested. Tests exist for comparing partially nonnested (overlapping) models, but this macro does not provide them. Clarke (2001) notes two models with the same functional form and the same error structure are strictly nonnested "if no variables in the first model can be written as a linear combination of the variables in the second model."
Vuong (1989) also provides definitions of nesting. He notes that models are strictly nonnested if they have "different distributional assumptions on the errors, say normally or logistic distributed" or if they have "the same distributional assumption but different functional forms" such as if one is linear and the other is nonlinear. Suppose two models have the same error distribution and functional form, and have one or more predictors in common. These models are partially, not strictly, nonnested and cannot be compared using the tests provided by this macro.
This macro is intended to compare strictly nonnested models that are estimated by ML procedures such as GENMOD, LOGISTIC, PROBIT, GLIMMIX, and others. Observations are assumed to be independent, so this macro is not intended to be used with repeated measures models or time series models.
Clarke (2007) suggests that for small sample sizes and when the observation log likelihood ratios have a peaked (leptokurtic) distribution, Vuong's test has lower power than his test.
Clarke's statistic is reported as (n+ - n-)/2, that is, as the number of positive values minus its expectation.
Note that information criteria such as Akaike's (AIC), Schwarz's (SC, BIC), and QIC can be used to compare competing nonnested models, but do not provide a test of the comparison. Consequently, they cannot indicate whether one model is significantly better than another. The GENMOD, LOGISTIC, GLIMMIX, MIXED, and other procedures provide information criteria measures.
Macro Updates
The %VUONG macro attempts to check for a later version of itself. If it is unable to do this (such as if there is no active Internet connection available), the macro issues the following message:
VUONG: Unable to check for newer version
The computations performed by the macro are not affected by the appearance of this message.
- LIMITATIONS:
- These tests require that both models are fit using exactly the same set of response values. This means more than just using the same response variable when fitting the models. See MISSING VALUES below. Data used to fit the competing models should consist of independent observations. When comparing nonnested models, the models must be strictly nonnested as described above. The Vuong and Clarke tests are not valid for nested or overlapping models. See Clarke (2001) and Vuong (1989) for details. The likelihood ratio test is not valid for nonnested models.
This macro cannot be used to analyze an input data set containing multiple BY groups. BY groups processing is not supported.
- MISSING VALUES:
- Missing values in the predictors or other variables involved in the model can cause one or more observations to be omitted when estimating the model. When competing models involve different variables, different observations might be omitted resulting in models not fit to exactly the same set of response values. The macro stops and issues an error message if it finds an observation in the input data set that has one predicted value missing and the other nonmissing. The macro proceeds with computations if both predicted values are either missing or nonmissing.
- SEE ALSO:
- For discussion and examples of comparing nested models using a CONTRAST statement, see Example 4 in "Examples of Writing CONTRAST and ESTIMATE Statements". See the %CLASSIFY macro that can help in constructing the input data set for the %VUONG macro when comparing ordinal logistic models as illustrated in Example 6 in the Results tab.
- REFERENCES:
- Clarke, K.A. (2001), "Testing Nonnested Models of International Relations: Reevaluating Realism," American Journal of Political Science, 45:3, 724-744.
Clarke, K.A. (2007), "A Simple Distribution-Free Test for Nonnested Hypotheses," Political Analysis, 15:3.
Clarke, K.A. and Signorino, C.S. (2010), "Discriminating Methods: Tests for Nonnested Discrete Choice Models," Political Studies, 58:2, 368-388.
Stokes, M. E., Davis, C. S., and Koch, G. G.
Vuong, Q. (1989), "Likelihood ratio tests for model selection and non-nested hypotheses," Econometrica, 57: 307-334.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
- EXAMPLE 1: Comparing Poisson and zero-inflated Poisson (ZIP) models
-
Long (1997) discusses a study that examines how factors such as gender (fem), marital status (mar), number of young children (kid5), prestige of the graduate program (phd), and number of articles published by a scientist's mentor (ment) affect the number of articles (art) published by the scientist. The data can be found in the SAS/ETS Sample Library. Poisson and negative binomial models based on these data are shown in the Getting Started section of the PROC COUNTREG documentation. ZIP and ZINB models are presented in the example titled "ZIP and ZINB Models for Data Exhibiting Extra Zeros" in the Examples section of the COUNTREG documentation.
These statements fit the Poisson and ZIP models to the data. These models can be compared using the Vuong and Clarke tests because the Poisson and ZIP models are not nested. The PROBZERO= option saves the zero-inflation probabilities in the OUTPUT OUT= data set. Notice that the OUTPUT OUT= data set (OUTZIP) is used as input to the COUNTREG step that fits the Poisson model. This allows the variables holding the predicted values and zero-inflation probabilities from the ZIP model to be passed to the OUTPUT OUT= data set (OUT) from the Poisson model that adds the requested predicted values from the Poisson model. Data set OUT has all of the information needed to compare the models.
proc countreg data=long97data; model art=fem mar kid5 phd ment / d=zip; zeromodel art~fem mar kid5 phd ment; output out=outzip pred=predzip probzero=p0; run; proc countreg data=outzip; model art=fem mar kid5 phd ment / d=Poisson; output out=out pred=predp; run;The %INC statement defines the VUONG macro and makes it available for use. Note that you only need to submit this statement once per SAS session. It will be omitted in subsequent examples. The following statement calls the %VUONG macro to compare the ZIP model to the Poisson model. The response distributions are specified in the DIST1= and DIST2= parameters and the variables containing the predicted values are specified in the P1= and P2= parameters. The numbers of parameters in the models are specified in the NPARM1= and NPARM2= parameters so that the adjusted tests can be computed.
%inc "<location of your file containing the VUONG macro>"; %vuong(data=out, response=art, model1=zip, p1=predzip, dist1=zip, pzero1=p0, model2=Poisson, p2=predp, dist2=poi, nparm1=12, nparm2=6)The large Z values and small p-values of the Vuong statistics indicate that one of the two models is closer to the true model. The positive values of the Z statistics indicate that it is the first model, the ZIP model, which is closer to the true model. In this case, the Clarke test does not reject the null hypothesis that the two models are equally far from the true model.
The Vuong Macro Model Information
Data Set out Response art Number of Observations Used 915 Model 1 zip Distribution ZIP Predicted Variable predzip Number of Parameters 12 Zero-inflation Probability p0 Log Likelihood -1604.7729 Model 2 Poisson Distribution POI Predicted Variable predp Number of Parameters 6 Log Likelihood -1651.0563
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred
ModelUnadjusted 4.1828 <.0001 zip Akaike Adjusted 3.6405 0.0003 zip Schwarz Adjusted 2.3340 0.0196 zip
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred Model Unadjusted 18.5000 0.2340 zip Akaike Adjusted 11.5000 0.4671 zip Schwarz Adjusted -0.5000 1.0000 Poisson - EXAMPLE 2: Comparing negative binomial and zero-inflated negative binomial (ZINB) models
-
Continuing Example 1, the following statements fit negative binomial and zero-inflated negative binomial (ZINB) models. Again, these models can be compared using the Vuong and Clarke tests because the negative binomial and ZINB models are not nested.
proc countreg data=long97data method=qn; model art=fem mar kid5 phd ment / d=zinb; zeromodel art~fem mar kid5 phd ment; output out=outzinb pred=pzinb probzero=p0; run; proc countreg data=outzinb method=qn; model art=fem mar kid5 phd ment / d=negbin(p=2); output out=out pred=pnb; run;The call to the %VUONG macro now must include the negative binomial dispersion parameter values, specified in the SCALE1= and SCALE2= macro parameters. These values appear in the PROC COUNTREG results labeled as _Alpha, Dispersion in PROC GENMOD, or Scale in PROC GLIMMIX.
%vuong(data=out, response=art, model1=zinb, p1=pzinb, dist1=zinb, scale1=0.376681, pzero1=p0, model2=neg. bin., p2=pnb, dist2=nb, scale2=0.441620, nparm1=13, nparm2=7)Both sets of test results are more ambiguous in this case since the unadjusted tests suggest the ZINB model is closer to the true model, the Schwarz adjusted tests suggest the negative binomial model is closer, and the Akaike adjusted tests find no difference.
The Vuong Macro Model Information
Data Set out Response art Number of Observations Used 915 Model 1 zinb Distribution ZINB Predicted Variable pzinb Number of Parameters 13 Scale 0.376681 Zero-inflation Probability p0 Log Likelihood -1549.9909 Model 2 neg. bin. Distribution NB Predicted Variable pnb Number of Parameters 7 Scale 0.441620 Log Likelihood -1560.9583
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred Model Unadjusted 2.2431 0.0249 zinb Akaike Adjusted 1.0159 0.3097 zinb Schwarz Adjusted -1.9407 0.0523 neg. bin.
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred Model Unadjusted 43.5000 0.0044 zinb Akaike Adjusted 7.5000 0.6435 zinb Schwarz Adjusted -44.5000 0.0036 neg. bin. - EXAMPLE 3: Comparing spline and polynomial models
-
The data below are presented in the "Getting Started" section of the GAM documentation from a study investigating the dependence of serum C-peptide concentration (logCP) at diagnosis on age and base deficit (a measure of acidity).
data diabetes; input Age BaseDeficit CPeptide @@; logCP = log(CPeptide); datalines; 5.2 -8.1 4.8 8.8 -16.1 4.1 10.5 -0.9 5.2 10.6 -7.8 5.5 10.4 -29.0 5.0 1.8 -19.2 3.4 12.7 -18.9 3.4 15.6 -10.6 4.9 5.8 -2.8 5.6 1.9 -25.0 3.7 2.2 -3.1 3.9 4.8 -7.8 4.5 7.9 -13.9 4.8 5.2 -4.5 4.9 0.9 -11.6 3.0 11.8 -2.1 4.6 7.9 -2.0 4.8 11.5 -9.0 5.5 10.6 -11.2 4.5 8.5 -0.2 5.3 11.1 -6.1 4.7 12.8 -1.0 6.6 11.3 -3.6 5.1 1.0 -8.2 3.9 14.5 -0.5 5.7 11.9 -2.0 5.1 8.1 -1.6 5.2 13.8 -11.9 3.7 15.5 -0.7 4.9 9.8 -1.2 4.8 11.0 -14.3 4.4 12.4 -0.8 5.2 11.1 -16.8 5.1 5.1 -5.1 4.6 4.8 -9.5 3.9 4.2 -17.0 5.1 6.9 -3.3 5.1 13.2 -0.7 6.0 9.9 -3.3 4.9 12.5 -13.6 4.1 13.2 -1.9 4.6 8.9 -10.0 4.9 10.8 -13.5 5.1 ;These statements fit a model using splines for both the Age and BaseDeficit predictors. The EFFECT statement specifies separate splines for each predictor and the resulting set of design columns is named SPL for use in the MODEL statement. The STORE statement saves the model for later use by PROC PLM and the OUTPUT statement saves the predicted values in data set SPLOUT. The NOREML option in the PROC GLIMMIX statement requests maximum likelihood estimation.
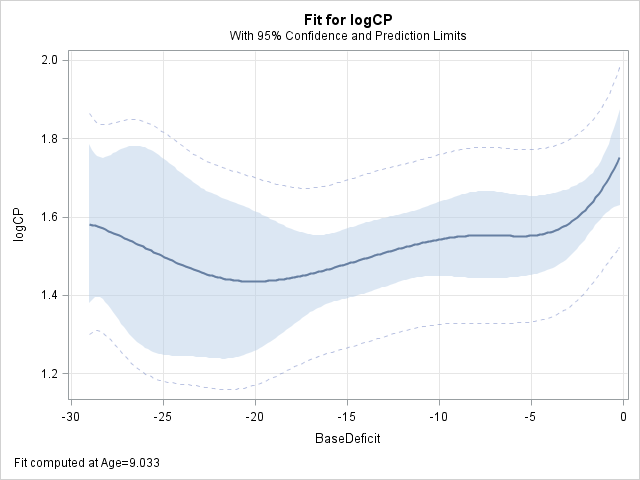
proc glimmix data=diabetes noreml; effect spl=spline(Age BaseDeficit / separate); model logCP = spl / s; store out=splmod; output out=splout pred(ilink)=splp; run;These EFFECTPLOT statements in PROC PLM provide plots of the fitted values against each of the predictors. The effects in each case appear to be at least quadratic in nature.
proc plm source=splmod; effectplot fit(x=Age); effectplot fit(x=BaseDeficit); run;
A polynomial model that is quadratic in each predictor is fitted using the following statements. Note that the output data set from the preceding GLIMMIX step is used as input for the next GLIMMIX step. The predicted values from both models are saved in data set FITS.
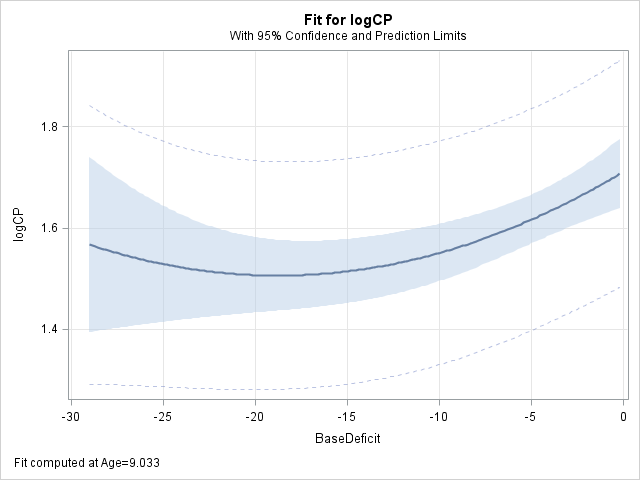
proc glimmix data=splout noreml; model logCP = Age|Age BaseDeficit|BaseDeficit / s; store out=quadmod; output out=fits pred(ilink)=quadp; run;The effect plots from this polynomial model are now strictly quadratic as compared to the plots from the spline model above.
proc plm source=quadmod; effectplot fit(x=Age); effectplot fit(x=BaseDeficit); run;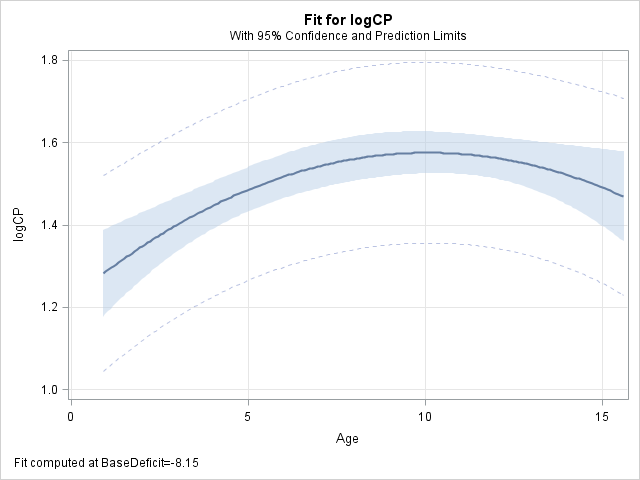
The %VUONG macro is called to compare the two models. The scale parameter reported by GLIMMIX is the square of the value needed by the macro. The square roots of the scale parameters are specified below.
%vuong(data=fits, response=logCP, model1=spline, p1=splp, dist1=nor, scale1=.0967, model2=quadratic, p2=quadp, dist2=nor, scale2=.1058, nparm1=14, nparm2=6)The Vuong Macro Model Information
Data Set fits Response logCP Number of Observations Used 43 Model 1 spline Distribution NOR Predicted Variable splp Number of Parameters 14 Scale .0967 Log Likelihood 39.4574491 Model 2 quadratic Distribution NOR Predicted Variable quadp Number of Parameters 6 Scale .1058 Log Likelihood 35.5573683
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred Model Unadjusted 1.4408 0.1496 spline Akaike Adjusted -1.5147 0.1299 quadratic Schwarz Adjusted -4.1173 <.0001 quadratic
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred Model Unadjusted 7.5000 0.0315 spline Akaike Adjusted -7.5000 0.0315 quadratic Schwarz Adjusted -14.5000 <.0001 quadratic - EXAMPLE 4: Comparing models with different link functions
-
The following data set contains a gamma-distributed response, Y, generated from a log-linked model involving predictor variables A and B and their interaction.
data a; do n=1 to 3; do a=-1 to 1 by .25; do b=1 to 4 by .5; lmu=2 + 4*a + 2*b - a*b; mu=exp(lmu); lambda=2; y=lambda*rand("gamma",mu); output; end; end; end; run; data a; input a b y @@; datalines; -1.00 1.0 6.69 0.50 4.0 44161.64 0.00 3.5 16166.42 -0.50 3.0 3543.95 -1.00 1.5 17.27 0.75 1.0 1045.21 0.00 4.0 44712.33 -0.50 3.5 12540.08 -1.00 2.0 98.99 0.75 1.5 1997.90 0.25 1.0 249.86 -0.50 4.0 43681.60 -1.00 2.5 499.28 0.75 2.0 3667.85 0.25 1.5 534.84 -0.25 1.0 60.39 -1.00 3.0 2229.24 0.75 2.5 6763.92 0.25 2.0 1329.38 -0.25 1.5 185.95 -1.00 3.5 10033.70 0.75 3.0 12539.73 0.25 2.5 3126.08 -0.25 2.0 484.98 -1.00 4.0 43601.68 0.75 3.5 23545.79 0.25 3.0 7503.28 -0.25 2.5 1575.45 -0.75 1.0 3.04 0.75 4.0 44205.64 0.25 3.5 18342.57 -0.25 3.0 4596.44 -0.75 1.5 52.89 1.00 1.0 2203.10 0.25 4.0 44091.60 -0.25 3.5 14033.04 -0.75 2.0 177.38 1.00 1.5 3725.16 0.50 1.0 527.22 -0.25 4.0 43699.68 -0.75 2.5 719.42 1.00 2.0 5902.46 0.50 1.5 993.48 0.00 1.0 107.35 -0.75 3.0 2659.39 1.00 2.5 9714.89 0.50 2.0 2217.75 0.00 1.5 295.58 -0.75 3.5 11436.84 1.00 3.0 16234.10 0.50 2.5 4612.23 0.00 2.0 791.36 -0.75 4.0 43724.48 1.00 3.5 26843.77 0.50 3.0 9954.23 0.00 2.5 2220.09 -0.50 1.0 42.07 1.00 4.0 44348.60 0.50 3.5 20545.31 0.00 3.0 5981.62 -0.50 1.5 69.98 -1.00 1.0 10.61 0.50 4.0 43978.08 0.00 3.5 16318.15 -0.50 2.0 263.82 -1.00 1.5 25.06 0.75 1.0 1050.88 0.00 4.0 44204.46 -0.50 2.5 1082.24 -1.00 2.0 85.42 0.75 1.5 1913.49 0.25 1.0 204.77 -0.50 3.0 3599.48 -1.00 2.5 511.68 0.75 2.0 3682.33 0.25 1.5 556.71 -0.50 3.5 12978.21 -1.00 3.0 2343.00 0.75 2.5 6707.24 0.25 2.0 1281.70 -0.50 4.0 44174.61 -1.00 3.5 9855.94 0.75 3.0 12784.85 0.25 2.5 3097.86 -0.25 1.0 55.68 -1.00 4.0 44348.73 0.75 3.5 23512.51 0.25 3.0 7679.94 -0.25 1.5 186.46 -0.75 1.0 5.75 0.75 4.0 43709.99 0.25 3.5 18561.98 -0.25 2.0 477.29 -0.75 1.5 51.84 1.00 1.0 2150.43 0.25 4.0 44294.88 -0.25 2.5 1519.93 -0.75 2.0 191.58 1.00 1.5 3613.19 0.50 1.0 591.90 -0.25 3.0 4544.84 -0.75 2.5 656.39 1.00 2.0 6117.25 0.50 1.5 1063.41 -0.25 3.5 14238.08 -0.75 3.0 2836.08 1.00 2.5 9725.04 0.50 2.0 2205.77 -0.25 4.0 43637.18 -0.75 3.5 11042.66 1.00 3.0 15928.60 0.50 2.5 4772.31 0.00 1.0 85.70 -0.75 4.0 43940.52 1.00 3.5 26521.27 0.50 3.0 9724.22 0.00 1.5 324.63 -0.50 1.0 21.07 1.00 4.0 43955.38 0.50 3.5 20578.18 0.00 2.0 790.34 -0.50 1.5 91.79 -1.00 1.0 6.28 0.50 4.0 43944.68 0.00 2.5 2273.70 -0.50 2.0 308.27 -1.00 1.5 19.47 0.75 1.0 963.03 0.00 3.0 5860.04 -0.50 2.5 1003.53 -1.00 2.0 96.20 0.75 1.5 1967.91 0.00 3.5 16209.48 -0.50 3.0 3621.42 -1.00 2.5 576.61 0.75 2.0 3674.94 0.00 4.0 44191.62 -0.50 3.5 12726.22 -1.00 3.0 2161.17 0.75 2.5 6526.27 0.25 1.0 230.35 -0.50 4.0 44017.85 -1.00 3.5 9534.02 0.75 3.0 12523.79 0.25 1.5 546.22 -0.25 1.0 39.97 -1.00 4.0 43806.75 0.75 3.5 23742.13 0.25 2.0 1431.56 -0.25 1.5 157.14 -0.75 1.0 16.04 0.75 4.0 43692.37 0.25 2.5 3189.81 -0.25 2.0 503.54 -0.75 1.5 61.58 1.00 1.0 2283.30 0.25 3.0 7824.22 -0.25 2.5 1528.93 -0.75 2.0 183.38 1.00 1.5 3585.20 0.25 3.5 18386.49 -0.25 3.0 4630.77 -0.75 2.5 755.26 1.00 2.0 5845.74 0.25 4.0 43788.15 -0.25 3.5 14345.90 -0.75 3.0 2803.06 1.00 2.5 9764.83 0.50 1.0 464.31 -0.25 4.0 43985.15 -0.75 3.5 10883.26 1.00 3.0 16655.93 0.50 1.5 1063.22 0.00 1.0 109.58 -0.75 4.0 43262.62 1.00 3.5 26782.57 0.50 2.0 2137.70 0.00 1.5 312.72 -0.50 1.0 27.90 1.00 4.0 43904.04 0.50 2.5 4618.40 0.00 2.0 769.80 -0.50 1.5 96.16 0.50 3.0 9746.06 0.00 2.5 2156.44 -0.50 2.0 325.90 0.50 3.5 20689.75 0.00 3.0 5928.10 -0.50 2.5 1080.56 ;The GENMOD steps below fit two competing models that differ only in their link functions. The first model uses the log link that is commonly employed with gamma models. The second model uses the reciprocal link function. This is the canonical link function for the gamma distribution and is the default in PROC GENMOD. The %VUONG macro compares the two models. Since both models have the same number of parameters estimated, the Akaike and Schwarz adjusted statistics would be the same as the unadjusted statistic, so the NPARM1= and NPARM2= options are omitted.
proc genmod data=a; model y=a b / dist=gamma link=log; output out=outlog p=plog; run; proc genmod data=outlog; model y=a b / dist=gamma; output out=fits p=pinv; run; %vuong(data=fits, response=y, model1=Gamma Log Link, p1=plog, dist1=gam, scale1=2.4933, model2=Gamma Reciprocal Link, p2=pinv, dist2=gam, scale2=0.8007)The results from both tests indicate that the log-linked model is the preferred model. This is as expected since the true model uses the log link.
The Vuong Macro Model Information
Data Set fits Response y Number of Observations Used 189 Model 1 Gamma Log Link Distribution GAM Predicted Variable plog Scale 2.4933 Log Likelihood -1648.3199 Model 2 Gamma Reciprocal Link Distribution GAM Predicted Variable pinv Scale 0.8007 Log Likelihood -1779.7125
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred Model Unadjusted 9.8312 <.0001 Gamma Log Link
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred Model Unadjusted 67.5000 <.0001 Gamma Log Link - EXAMPLE 5: Comparing models with different error distributions
-
Using the data from the previous example, the following GENMOD steps fit models using either the gamma or the inverse Gaussian distributions, both of which are commonly used for positively valued responses. The model specifications are otherwise identical, so again there is no need to request the adjusted statistics.
proc genmod data=a; model y=a b / dist=gamma link=log; output out=outgam p=pgam; run; proc genmod data=outgam; model y=a b / dist=ig link=log; output out=fits p=pinvg; run; %vuong(data=fits, response=y, model1=Gamma, p1=pgam, dist1=gam, scale1=2.4933, model2=Inv. Gaussian, p2=pinvg, dist2=ig, scale2=0.0413)Both tests indicate a preference for the gamma model, which was the distribution used in generating the data.
The Vuong Macro Model Information
Data Set fits Response y Number of Observations Used 189 Model 1 Gamma Distribution GAM Predicted Variable pgam Scale 2.4933 Log Likelihood -1648.3199 Model 2 Inv. Gaussian Distribution IG Predicted Variable pinvg Scale 0.0413 Log Likelihood -1846.856
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred
ModelUnadjusted 3.6907 0.0002 Gamma
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred
ModelUnadjusted 49.5000 <.0001 Gamma - EXAMPLE 6: Comparing ordinal (cumulative logit) and nominal (generalized logit) logistic models
-
Stokes et. al. (2000) analyze dental pain relief data from a study by Gansky, Koch, and Wilson (1994). The response is pain relief on a five-point scale, 0 to 4 with 0 indicating no relief and 4 maximum relief.
The following statements fit the generalized logit model that treats the response levels as nominal (unordered). This model is often used when the response levels are actually ordinal (ordered) but a test of the proportional odds assumption is rejected when fitting the usual proportional odds model. However, the generalized logit model contains many more parameters since no equality restriction is placed on the parameters within an effect as in the proportional odds model.
proc logistic data=dent; class center baseline trt / param=ref order=data; model resp(descending)=center baseline trt / link=glogit; output out=log p=pglog; run;With an ordinal response, the P= option in the OUTPUT statement of PROC LOGISTIC creates a data set in which each input observation results in several output observations with the predicted probabilities of the individual levels stored in the P= variable. The following statements keep only the observation containing predicted probability of the observed level. These are the values needed in the %VUONG macro for this model.
data log1; set log; if resp=_level_; drop _level_; run;The proportional odds model is fitted in the next PROC LOGISTIC step. The proportional odds model fits cumulative, rather than generalized, logits and is commonly used for ordinal responses such as the pain relief response in this example. It is the default model fit by PROC LOGISTIC when the response has more than two levels.
proc logistic data=log1; class center baseline trt / param=ref order=data; model resp(descending)=center baseline trt; output out=fits p=ppo; run;As before, the P= option creates a data set with multiples of each input observation. But when the response is ordinal, the probabilities in the P= variable are cumulative probabilities. In order to get the predicted probability of the observed level, you can use the POBS= parameter in the %CLASSIFY macro. To use the %CLASSIFY macro, specify the output data set from PROC LOGISTIC in the DATA= parameter, the response variable in the RESPONSE= parameter, and the variable of cumulative probabilities in the P= parameter. In the OUT= parameter, specify a name for the data set that the %CLASSIFY macro creates, and in the POBS= parameter assign a name to the variable that will contain the predicted probability of the observed response.
%inc "<location of your file containing the CLASSIFY macro>"; %classify(data=fits, response=resp, p=ppo, pobs=pobs, out=probs)The %VUONG macro can now be called to compare the models. Since the multilevel response modeled by both the generalized logit and the proportional odds model is a multinomial response, specify DIST=MULT for both models.
%vuong(data=probs, response=resp, model1=Generalized Logit, p1=pglog, dist1=mult, model2=Proportional Odds, p2=pobs, dist2=mult, nparm1=28,nparm2=10)The unadjusted tests both indicate that the generalized logit model is the preferred model if you ignore the model sizes. But because the generalized logit model has so many more parameters, the penalty applied by the adjusted tests swing the conclusion the other way. Again, you might want to further investigate the model fits, such as by comparing predicted probabilities at the observation level, before choosing a model.
The Vuong Macro Model Information
Data Set probs Response resp Number of Observations Used 258 Model 1 Generalized Logit Distribution MULT Predicted Variable pglog Number of Parameters 28 Log Likelihood -326.67394 Model 2 Proportional Odds Distribution MULT Predicted Variable pobs Number of Parameters 10 Log Likelihood -344.41297
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred Model Unadjusted 3.1927 0.0014 Generalized Logit Akaike Adjusted -0.0470 0.9625 Proportional Odds Schwarz Adjusted -5.8021 <.0001 Proportional Odds
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred Model Unadjusted 38.0000 <.0001 Generalized Logit Akaike Adjusted -20.0000 0.0150 Proportional Odds Schwarz Adjusted -52.0000 <.0001 Proportional Odds Note that fitting partial proportional and nonproportional odds models is discussed and illustrated in this note. You can compare proportional odds, partial proportional odds, and nonproportional odds models using likelihood ratio tests or F-tests since these are nested models.
- EXAMPLE 7: Comparing generalized Poisson and negative binomial models
-
The generalized Poisson distribution is an extension of the Poisson distribution. It includes a scale parameter, ξ, which allows for overdispersion. When ξ=0, the generalized Poisson reduces to the Poisson distribution. A model using this distribution is another alternative to negative binomial and zero-inflated models. Though this distribution is not directly supported by any modeling procedure, you can fit such a model by specifying the log likelihood of the generalized Poisson distribution in the NLMIXED procedure.
The following statements fit a generalized Poisson model to the articles data from Examples 1 and 2. Since this distribution is not available in the %VUONG macro, it is necessary to specify DIST1=OTH and to provide the likelihood contributions of the observations, rather than predicted responses, in the P1= variable. The PREDICT statement below computes these probabilities by exponentiating the log likelihood values. The probabilities are saved in a data set named GENPOI in a variable named PRED.
proc nlmixed data=long97data; parms b0=0 b1=0 b2=0 b3=0 b4=0 b5=0 xi=0; mean = exp(b0 + b1*fem + b2*mar + b3*kid5 + b4*phd + b5*ment); ll = log(mean*(1-xi)) + (art-1)*log(mean-xi*(mean-art)) - (mean-xi*(mean-art)) - lgamma(art+1); model art ~ general(ll); predict exp(ll) out=genpoi; run;The negative binomial model is fit as in Example 2 and predicted responses are saved in variable PNB.
proc countreg data=genpoi method=qn; model art=fem mar kid5 phd ment / d=negbin(p=2); output out=out pred=pnb; run;The %VUONG macro compares the two models. Both models have seven parameters, so the adjusted statistics are not requested.
%vuong(data=out, response=art, model1=Gen. Poisson, p1=pred, dist1=oth, model2=Neg. Binomial, p2=pnb, dist2=nb, scale2=0.441620)The results from both tests indicate no significant difference between the two models.
The Vuong Macro Model Information
Data Set out Response art Number of Observations Used 915 Model 1 Gen. Poisson Distribution OTH Predicted Variable pred Log Likelihood -1563.8691 Model 2 Neg. Binomial Distribution NB Predicted Variable pnb Scale 0.441620 Log Likelihood -1560.9583
The Vuong Macro Vuong Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Vuong Statistic Z Pr>|Z| Preferred Model Unadjusted -0.6918 0.4890 Neg. Binomial
The Vuong Macro Clarke Sign Test H0: models are equally close to the true model Ha: one of the models is closer to the true model
Clarke Statistic M Pr>=|M| Preferred Model Unadjusted -9.5000 0.5518 Neg. Binomial - EXAMPLE 8: Comparing nested models with a likelihood ratio test
-
Example 4 of this note illustrates comparing nested models using the CONTRAST statement in the procedure used to fit the models. The %VUONG macro can also perform the test without the need of determining proper contrast coefficients. As shown in the example, the following statements fit the full model containing all main effects and interactions, and a reduced model containing only main effects. The %VUONG macro is called with the TEST=LR parameter requesting the likelihood ratio test to compare the two nested models. Note the use of the FREQ= parameter since the models were fit to summarized data containing a frequency count variable.
proc genmod data=detergent; class Softness Previous Temperature; freq Count; model Brand = Softness|Previous|Temperature / dist=binomial; output out=full p=pfull; run; proc genmod data=full; class Softness Previous Temperature; freq Count; model Brand = Softness Previous Temperature / dist=binomial; output out=fullred p=pred; run; %vuong(data=fullred, freq=count, response=Brand, event='M', test=lr, model1=Full, p1=pfull, dist1=bin, nparm1=12, model2=Reduced, p2=pred, dist2=bin, nparm2=5)The likelihood ratio test is not significant indicating insufficient evidence to prefer the more complex model over the simpler main effects model. Note that the results agree with the likelihood ratio test produced by the CONTRAST statement illustrated in Example 4 of the note.
The Vuong Macro Model Information
Data Set fullred Response Brand Event Level M Number of Trials 1 Frequency Variable count Number of Observations Used 24 Model 1 Full Distribution BIN Predicted Variable pfull Number of Parameters 12 Log Likelihood -682.2478 Model 2 Reduced Distribution BIN Predicted Variable pred Number of Parameters 5 Log Likelihood -686.36179
The Vuong Macro Likelihood Ratio Test H0: models are equivalent Ha: models differ
Test Chi-Square DF Pr>Chi-Square Likelihood Ratio 8.2280 7 0.3129
Right-click on the link below and select Save to save the %VUONG macro definition to a file. It is recommended that you name the file vuong.sas.
| Type: | Sample |
| Topic: | Analytics ==> Categorical Data Analysis Analytics ==> Regression |
| Date Modified: | 2019-05-07 15:24:40 |
| Date Created: | 2011-02-24 15:13:27 |
Operating System and Release Information
| Product Family | Product | Host | SAS Release | |
| Starting | Ending | |||
| SAS System | SAS/STAT | z/OS | ||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| SAS System | SAS/ETS | z/OS | ||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||