Usage Note 41364: ROC analysis for binary response models fit in the GLIMMIX, NLMIXED, GAM or other procedures
 |  |  |
While the GLIMMIX and NLMIXED procedures can fit a logistic model, with or without random effects, they cannot produce a graph of the associated ROC (Receiver Operating Characteristic) curve, nor compute the area under the ROC curve (AUC). Similarly, PROC GAM can fit a logistic model, with or without nonparametric components such as splines, but also cannot do an ROC analysis of the resulting model. You can obtain an ROC analysis from these, or any procedure or method that models a binary response (such as the GENMOD or PROBIT procedures), by saving the predicted probabilities from the fitted model and using them in PROC LOGISTIC in the MODEL or ROC statements. PROC LOGISTIC can then provide a graph of the ROC curve and the AUC. Tests comparing the ROC curves from competing models can also be performed in PROC LOGISTIC. This is illustrated in the examples below. Another method used for binary response data is the classification tree. Beginning in SAS® 9.4 TS1M3, you can build a classification tree using PROC HPSPLIT and obtain an ROC analysis. For discussion and an example, see the PROC HPSPLIT documentation.
For an extension of the AUC for multinomial models, see the MultAUC macro.
For information on obtaining an unbiased ROC analysis using validation data or crossvalidation, see this note.
This example shows how to produce a graph of overlaid ROC curves from competing models fit to a single data set. This note shows how you can create a graph of overlaid ROC curves of a single model applied to multiple data sets.
A logistic model with random effects
The following statements create the data set, MULTICENTER, which contains the number of subjects exhibiting side effects (SIDEEFFECT) and the total number of subjects (N) in each center (CENTER). The centers are divided into two groups (GROUP).
data multicenter;
input center group$ n sideeffect @@;
datalines;
1 A 32 14 1 B 33 18 2 A 30 4 2 B 28 8
3 A 23 14 3 B 24 9 4 A 22 7 4 B 22 10
5 A 20 6 5 B 21 12 6 A 19 1 6 B 20 3
7 A 17 2 7 B 17 6 8 A 16 7 8 B 15 9
9 A 13 1 9 B 14 5 10 A 13 3 10 B 13 1
11 A 11 1 11 B 12 2 12 A 10 1 12 B 9 0
13 A 9 2 13 B 9 6 14 A 8 1 14 B 8 1
15 A 7 1 15 B 8 0
;
These statements fit a logistic model with a random effect for centers. Predicted log odds (XBETA) and predicted probabilities (PREDPROB) are computed by the OUTPUT statement and saved in data set GLMMOUT.
proc glimmix data=multicenter;
class center group;
model sideeffect/n = group / dist=binomial solution;
random intercept / subject=center solution;
output out=glmmout pred=xbeta pred(ilink)=predprob;
run;
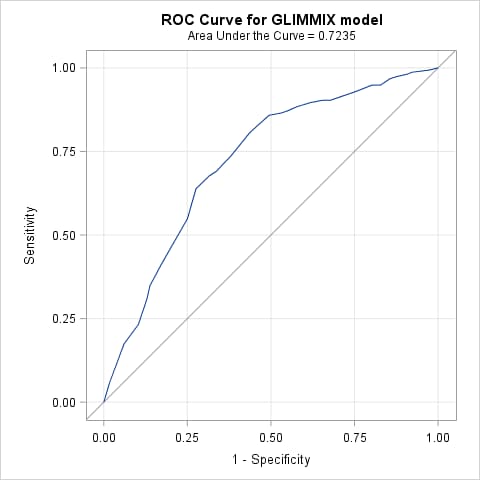
Beginning in SAS 9.4 TS1M3, you can use the ROC statement with the NOFIT option in the MODEL statement to obtain the ROC analysis of the GLIMMIX model. The following statements use PROC LOGISTIC to perform the ROC analysis using the predicted probabilities from PROC GLIMMIX. While a MODEL statement is required, the NOFIT option avoids fitting the specified model (an intercept-only model in this case) since this is not needed. The PRED= option in the ROC statement enables use of the predicted probabilities from GLIMMIX to provide an ROC analysis. When the PRED= option is used, the variable specified does not need to be in the MODEL statement. Otherwise, variables in the ROC statement must appear in the MODEL statement.
proc logistic data=glmmout;
model sideeffect/n = / nofit;
roc "GLIMMIX model" pred=predprob;
run;
|
||||||||||||||||||||||||||||
Prior to SAS 9.4 TS1M3, the ROC analysis can be done by using either the predicted log odds or the predicted probabilities as the single predictor in the MODEL statement. The PLOTS(ONLY)=ROC option produces a graph of the ROC curve. The area under the ROC curve is displayed at the top of the graph.
proc logistic data=glmmout plots(only)=roc;
model sideeffect/n = predprob;
run;
A logistic model with spline effects
These data are introduced in the example titled Generalized Additive Model with Binary Data in the PROC GAM documentation.
data kyphosis;
input Age StartVert NumVert Kyphosis @@;
datalines;
71 5 3 0 158 14 3 0 128 5 4 1
2 1 5 0 1 15 4 0 1 16 2 0
61 17 2 0 37 16 3 0 113 16 2 0
59 12 6 1 82 14 5 1 148 16 3 0
18 2 5 0 1 12 4 0 243 8 8 0
168 18 3 0 1 16 3 0 78 15 6 0
175 13 5 0 80 16 5 0 27 9 4 0
22 16 2 0 105 5 6 1 96 12 3 1
131 3 2 0 15 2 7 1 9 13 5 0
12 2 14 1 8 6 3 0 100 14 3 0
4 16 3 0 151 16 2 0 31 16 3 0
125 11 2 0 130 13 5 0 112 16 3 0
140 11 5 0 93 16 3 0 1 9 3 0
52 6 5 1 20 9 6 0 91 12 5 1
73 1 5 1 35 13 3 0 143 3 9 0
61 1 4 0 97 16 3 0 139 10 3 1
136 15 4 0 131 13 5 0 121 3 3 1
177 14 2 0 68 10 5 0 9 17 2 0
139 6 10 1 2 17 2 0 140 15 4 0
72 15 5 0 2 13 3 0 120 8 5 1
51 9 7 0 102 13 3 0 130 1 4 1
114 8 7 1 81 1 4 0 118 16 3 0
118 16 4 0 17 10 4 0 195 17 2 0
159 13 4 0 18 11 4 0 15 16 5 0
158 15 4 0 127 12 4 0 87 16 4 0
206 10 4 0 11 15 3 0 178 15 4 0
157 13 3 1 26 13 7 0 120 13 2 0
42 6 7 1 36 13 4 0
;
These statements fit a logistic model using 3 degree of freedom splines for each of the predictors. The predicted values are saved in data set GAMOUT as the variable named P_Kyphosis.
proc gam data=kyphosis;
model Kyphosis (event="1") = spline(Age ,df=3)
spline(StartVert,df=3)
spline(NumVert ,df=3) / dist=binomial;
output out=gamout predicted;
run;
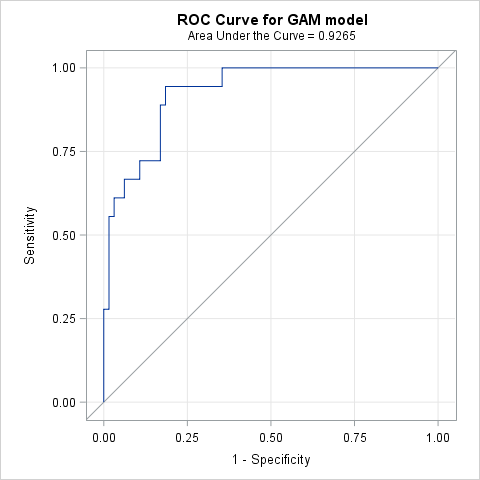
PROC LOGISTIC is used to do the ROC analysis by specifying P_Kyphosis in the PRED= option in the ROC statement.
proc logistic data=gamout;
model Kyphosis (event="1") = / nofit;
roc "GAM model" pred=P_Kyphosis;
run;
|
||||||||||||||||||||||||||||
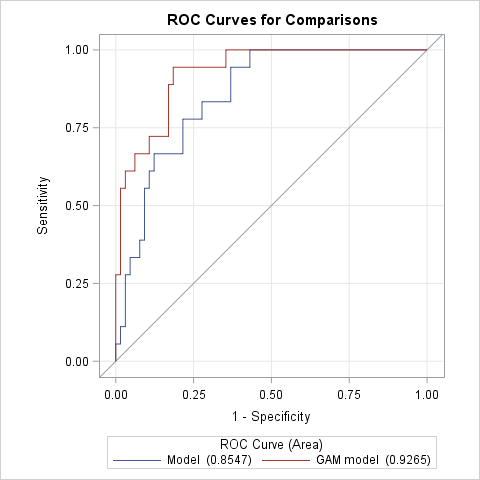
You can use the ROC and ROCCONTRAST statements in PROC LOGISTIC to compare the spline model to the corresponding linear effects logistic model that doesn't use splines. In the following statements, two models are estimated and compared. The MODEL statement specifies the linear effects logistic model. The ROC statement specifies the spline model from PROC GAM by using the predicted values variable, P_Kyphosis, in the PRED= option. Note that the PRED= variable must contain no missing values. If it does, then remove those observations from the DATA= data set prior to the PROC LOGISTIC step or omit them by including a WHERE statement. The ROCCONTRAST statement performs a test comparing the areas under the ROC curves of the two models.
proc logistic data=gamout;
model Kyphosis (event="1") = Age StartVert NumVert;
roc "GAM model" pred=P_Kyphosis;
roccontrast;
run;
PROC LOGISTIC produces a plot showing the ROC curves and areas from both models. The tables that follow provide confidence intervals around the areas under each ROC curve and a test comparing the areas. The small p-value (p=0.0166) indicates that the spline model fit in PROC GAM is a significantly better model than the simple linear effects model fit in PROC LOGISTIC.
|
||||||||||||||||||||||||||||||||||||||||||||||||
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | Microsoft Windows Server 2003 Enterprise Edition | ||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 95/98 | ||||
| OS/2 | ||||
| Microsoft® Windows® for x64 | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows XP Professional | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| OpenVMS VAX | ||||
| z/OS | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | SAS Reference ==> Procedures ==> GLIMMIX SAS Reference ==> Procedures ==> LOGISTIC Analytics ==> Categorical Data Analysis SAS Reference ==> Procedures ==> CATMOD SAS Reference ==> Procedures ==> GAM SAS Reference ==> Procedures ==> GENMOD SAS Reference ==> Procedures ==> NLMIXED SAS Reference ==> Procedures ==> PROBIT SAS Reference ==> Procedures ==> ADAPTIVEREG SAS Reference ==> Procedures ==> FMM SAS Reference ==> Procedures ==> GAMPL SAS Reference ==> Procedures ==> GEE SAS Reference ==> Procedures ==> HPFMM SAS Reference ==> Procedures ==> HPGENSELECT SAS Reference ==> Procedures ==> HPLOGISTIC SAS Reference ==> Procedures ==> HPNLMOD SAS Reference ==> Procedures ==> MDC SAS Reference ==> Procedures ==> QLIM SAS Reference ==> Procedures ==> SURVEYLOGISTIC Analytics ==> Regression Analytics ==> Statistical Graphics |
| Date Modified: | 2020-01-10 15:32:42 |
| Date Created: | 2010-10-22 03:04:22 |