Usage Note 37944: Plotting empirical (observed) logits for binary and ordinal response data
 |  |  |
For binary response data, there is a single logit which is defined as
Logit = log[ p/(1-p) ],
where p is the probability of the event level of the response.
The proportional odds assumption for an ordinal, multinomial logistic model implies that the curves on the various cumulative logits are parallel. This assumption can be assessed visually for a given predictor by plotting it against the empirical cumulative logits.
For a response with k levels, the cumulative logits are:
Logit1 = log[ p1/(1-p1) ] = log[ p1/(p2+p3+...+pk) ] ,
Logit2 = log[ (p1+p2)/(1-(p1+p2)) ] = log[ (p1+p2)/(p3+p4+...+pk) ] ,
...
Logitk-1 = log[ (p1+p2+...+pk-1) / pk ]
where p1, p2, ... , pk are the probabilities of the k response levels in a population. A population is defined as a setting of the predictors. Notice that there are k-1 cumulative logits defined on the k response levels. Effectively, each cumulative logit dichotomizes the multinomial response into two sums by "cutting" the ordered list of probabilities at each possible position.
By using the observed counts, yi, you can compute empirical logits for use in plots. A constant, such as 0.5, can be added to the numerators and denominators of the logits when zero counts exist in the data that would cause a logit to be undefined.
EmpLogiti = log[ (y1+y2+...+yi+c)/(yi+1+yi+2+...+yk+c) ] ,
where c is a constant. This computation is easily done when there is some replication within the levels of the predictor, such as for predictors that are typically specified in the CLASS statement of the modeling procedure. The computation is illustrated in the code presented in the examples below. When the predictor is continuous, with little or no replication at each level, then the logits can be computed in neighborhoods of each observation using observations that have similar values of the predictor.
This note and Derr (2013) further discuss the testing and assessment of the proportional odds assumption. Derr presents macros that produce empirical logit plots like those shown below and plots proposed by Harrell (2001) which provide another way to visually assess proportional odds. An updated version of his empirical logit plotting macro that is more robust is available. See instructions in Example 1 below. When the proportional odds assumption is not valid, alternative models can be fit as discussed and illustrated in the above note and by Derr (2013).
Example 1: Cheese tasting data
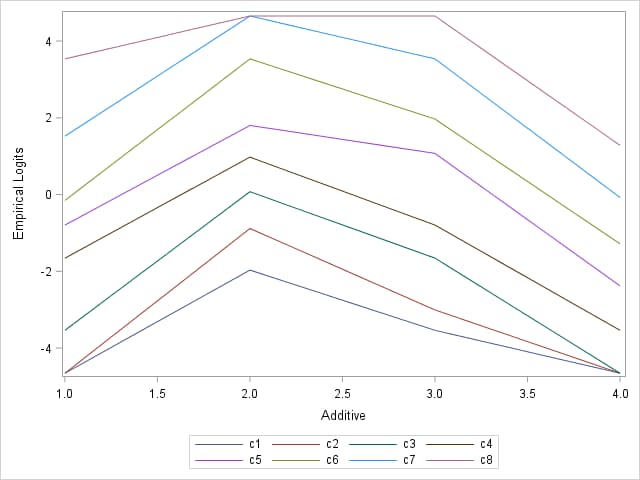
The following uses the data in the example titled "Ordinal Logistic Regression" in the LOGISTIC documentation. To compute the empirical logits, begin by transposing the data so that there is one observation per additive. Each observation contains the counts of all nine response categories for that additive. Since there are a few zero counts, the following DATA step adds 0.5 to the numerator and denominator of each cumulative logit. The eight empirical logits, c1, c2, ..., c8, are then computed. Note that each logit is computed by accumulating over the lower response levels. Finally, a plot of the empirical logits is produced using PROC SGPLOT.
proc transpose data=Cheese out=tran;
by Additive; var freq;
run;
data a; set tran;
const=0.5;
c1=log((sum(of col1-col1)+const)/(sum(of col2-col9)+const));
c2=log((sum(of col1-col2)+const)/(sum(of col3-col9)+const));
c3=log((sum(of col1-col3)+const)/(sum(of col4-col9)+const));
c4=log((sum(of col1-col4)+const)/(sum(of col5-col9)+const));
c5=log((sum(of col1-col5)+const)/(sum(of col6-col9)+const));
c6=log((sum(of col1-col6)+const)/(sum(of col7-col9)+const));
c7=log((sum(of col1-col7)+const)/(sum(of col8-col9)+const));
c8=log((sum(of col1-col8)+const)/(sum(of col9-col9)+const));
run;
proc sgplot;
series y=c1 x=Additive;
series y=c2 x=Additive;
series y=c3 x=Additive;
series y=c4 x=Additive;
series y=c5 x=Additive;
series y=c6 x=Additive;
series y=c7 x=Additive;
series y=c8 x=Additive;
yaxis label="Empirical Logits";
run;
Notice that the curves are roughly parallel. This visually confirms the nonsignificant test of the proportional odds assumption provided by PROC LOGISTIC (p=0.6936).
 |
Using the EmpiricalLogitPlot macro
The empirical logit plot can also be produced using an updated version of the EmpiricalLogitPlot macro provided by Derr (2013). To use this macro, submit all of this macro code, unaltered, in your SAS® session. Note that the EmpiricalLogitPlot macro calls two other macros whose code is also provided. Use of the macro also requires version 1.1 or later of the CtoN macro. The code for that macro must also be submitted in your SAS session. Once all of this macro code is submitted, the macros are available for use in your current SAS session. See the instructions and a description of the available macro parameters and options in the above macro code.
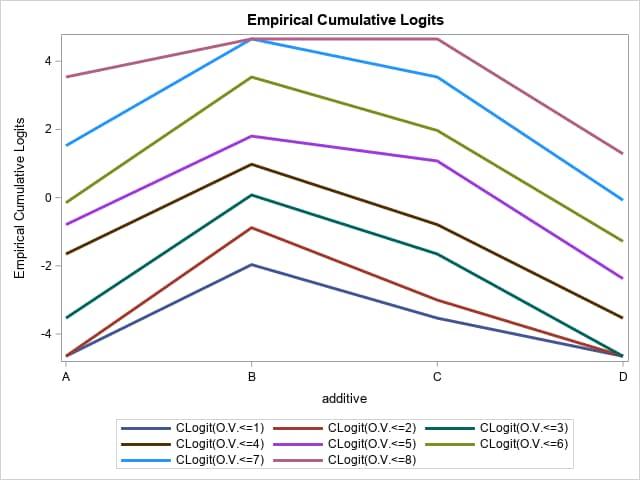
The macro associates the response levels with Ordered Values as shown in the Response Profile table. By default, the macro associates the higher response levels with the lower Ordered Values. This is what PROC LOGISTIC does when the DESCENDING option is used. The macro always computes logits over the response levels associated with the lower Ordered Values. This means that if, as in this example, the response levels have values 1, 2, ... , 9, then by default the logits are computed over the higher response levels because they are associated with the lower Ordered Values. Always inspect the Response Profile table to verify that the response levels are in logical increasing or decreasing order. Otherwise the plot is meaningless.
Note that the data in this example is aggregated such that each observation represents several actual observations. The count provided in variable freq indicates the number of times that each combination of additive and y values occurred. Since the macro does not accept aggregated data, it is necessary to expand the data to contain a single observation for each individual occurrence. The following DATA step expands the aggregated data.
data cheese;
set cheese;
do i=1 to freq;
output;
end;
run;
The following macro call produces the plot. Specify the response variable in y=. In x=, specify any predictors to plot empirical logits against. Recall that the default is to assign higher response levels to lower Ordered Values and that the macro always computes logits by accumulating over the lower Ordered Values. Therefore, in order for the logits to be computed over the lower response levels, the ascending option is needed to reverse the default association of Ordered Values. When logits are to be plotted against several predictors, it is useful to have all of the plots arranged in a panel and this is done by default by the macro. Separate plots for the predictors can be obtained with the nopanel option, which allows for the display of the predictor values on the horizontal axis.
%EmpiricalLogitPlot(data=cheese, y=y, x=additive, options=ascending nopanel)
 |
Example 2: Dental data
This example uses the dental pain relief data discussed in this note. For this ordinal, multinomial data, the overall test of the proportional odds assumption provided by PROC LOGISTIC is significant (p=0.0089). As mentioned in the note, this test is known to be liberal (rejecting the assumption more often than expected), particularly for small samples. While the rough sample size requirements as discussed by Stokes, et. al. are found to be nearly met by these data, separate tests of parallelism for each of the three predictors produced using PROC LOGISTIC (p=0.18, 0.17, and 0.07) suggest that not all of the predictors exhibit nonproportional odds. Of course, the overall test provided by PROC LOGISTIC having combined degrees of freedom is somewhat more powerful than each of these three tests. Graphical assessment of the assumption can be helpful.
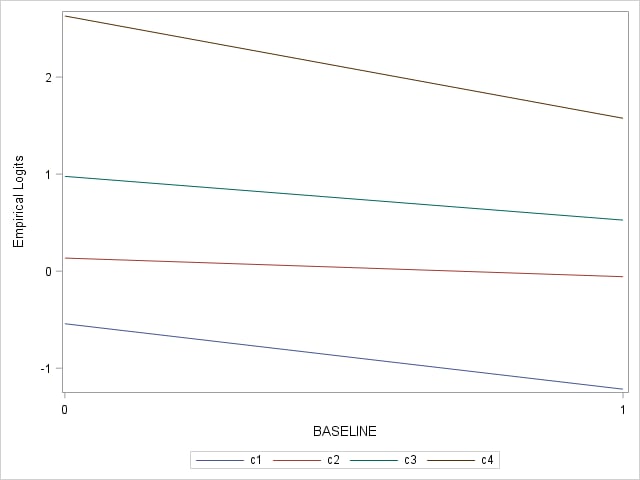
The following statements produce empirical logit plots for each of the three predictors – Baseline, Center, and Trt. Beginning with Baseline, these statements first obtain the response counts for each of the two levels of Baseline, then proceed as above to compute the empirical logits. For this data set there are no zero counts, so a constant is not added to the counts. Since there are five response levels, four logits are computed and plotted.
proc freq data=dent;
table baseline*resp / out=os;
run;
proc transpose data=os out=tran;
by baseline; var count;
run;
data a; set tran;
const=0;
c1=log((sum(of col1-col1)+const)/(sum(of col2-col5)+const));
c2=log((sum(of col1-col2)+const)/(sum(of col3-col5)+const));
c3=log((sum(of col1-col3)+const)/(sum(of col4-col5)+const));
c4=log((sum(of col1-col4)+const)/(sum(of col5-col5)+const));
run;
proc sgplot;
series y=c1 x=baseline;
series y=c2 x=baseline;
series y=c3 x=baseline;
series y=c4 x=baseline;
yaxis label="Empirical Logits";
xaxis integer;
run;
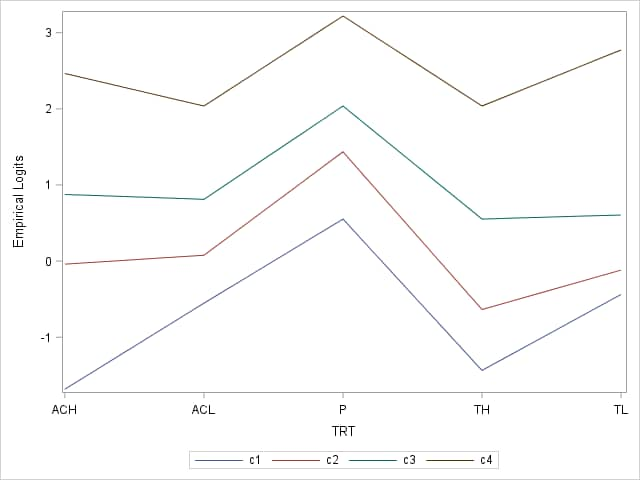
The test of parallelism for Baseline was not significant (p=0.1727). The plot shows only a little variation among the logit lines. Similar code is used to produce the plot for Trt and Center. For Trt, the test for parallelism was marginally significant (p=0.0688). The plot shows some nonparallelism at levels ACH and TL. For Center, the test for parallelism was not significant (p=0.1782). The plot shows roughly parallel lines.
 |
 |
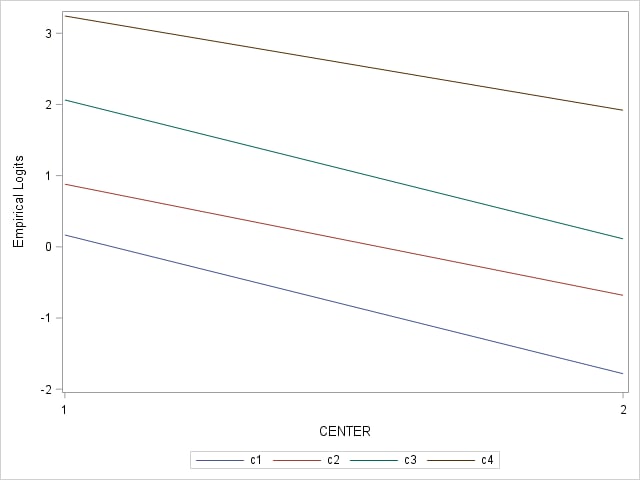 |
The EmpiricalLogitsPlot macro can produce the same set of plots and adds the ldose variable. As in the previous example, the ascending option is needed to compute logits over the lower levels of the response. The default is to produce a panel of all plots.
%EmpiricalLogitPlot(data=dent, y=resp, x=baseline trt center ldose,
const=0, options=ascending)
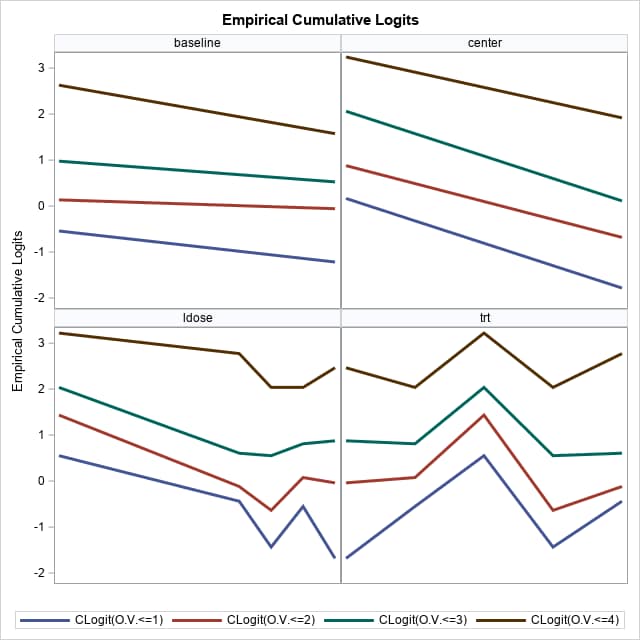 |
Example 3: Warmth of relationship data
Long (1997) presents data from a survey investigating the effects of demographic predictors such as race (White), Age, education (Ed), and occupational prestige (Prst) on the level of agreement with the statement that a working mother can have as warm a relationship with her child as a nonworking mother (Warm). Agreement can range from strongly disagree (Warm=1) to strongly agree (Warm=4). Since the probabilities of higher warmth are of interest, logits are to be computed over the higher response levels.
The overall test of the proportional odds assumption is marginally significant (p=0.0606). The assumption can be assessed graphically with the following call of the EmpiricalLogitPlot macro. Note that all of the predictors, other than race, are effectively continuous with many levels. For a predictor with a large number of levels (more than 20, by default, as controlled by contcutoff=), the macro defines neighborhoods around the observed values and represents each logit using a LOESS-smoothed curve. By default, the neighborhood size is 50 (controlled by neighbors=), but the macro might reduce it, depending on the sample size. When that happens, notes are displayed in the log. Also, the final neighborhood size is noted in each affected plot.
%EmpiricalLogitPlot(v,data=data9.longch5ordlog, y=Warm, x=White Age Ed Prst)
The Response Profile table shows that the default ordering of response levels was used, so logits are computed over the higher response levels (lower Ordered Values). The plots show good parallelism of the logits for three of the four predictors. Only Ed shows some difference.
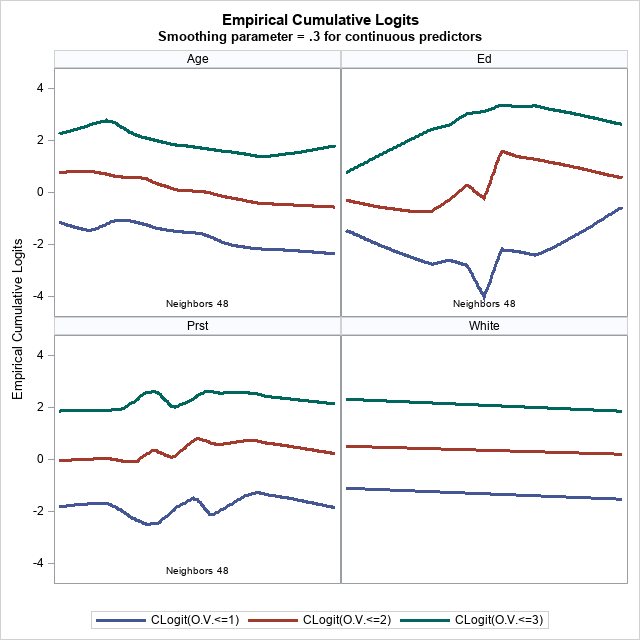 |
The following statements allow Ed to have unequal slopes in an ordinal logistic model for Warm.
proc logistic data=Longdat;
model Warm = Age White Ed Prst / unequalslopes=(Ed);
run;
Example 4: Insect data
These data are from the example titled "Multilevel Response" in the PROC PROBIT documentation. The response, Symptoms, has three ordered levels resulting in two cumulative logits. Two predictors, Prep and Ldose, are of interest.
If modeled in PROC LOGISTIC using a main effects logistic model, the test of the proportional odds assumption is not significant (p=0.2857). Similarly, using a probit model, the test for parallelism is also not significant (p=0.3402). After expanding this aggregated data so that there is a single response per observation, the following call of the EmpiricalLogitPlots macro produces plots of the observed logits. Note that the response variable is character with levels None, Mild, and Severe. If either the ascending or the default descending order is used, the levels will not be in logical ascending or descending order. Since the order of first appearance of the levels in the data set is in logical ascending order, the dataorder option can be used to ensure that the response levels are in logical order.
data multi;
set multi;
do i=1 to n;
output;
end;
run;
%EmpiricalLogitPlot(data=multi, y=symptoms, x=prep ldose, options=dataorder, const=0)
Proper response ordering is confirmed by the Response Profile table.The resulting plots are reasonably consistent with the nonsignificant test for proportion odds.
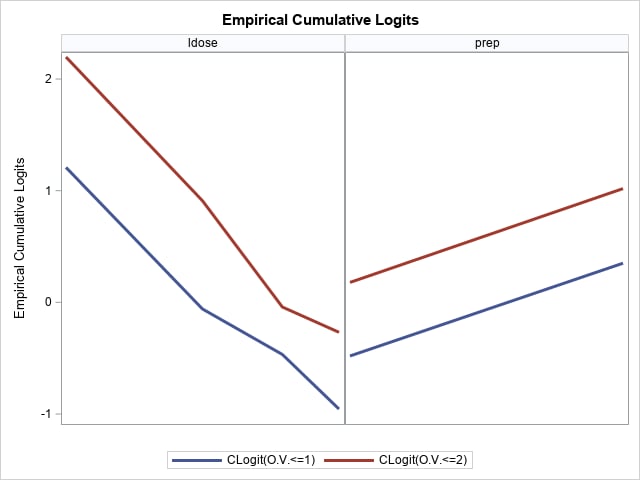 |
Example 5: Binary response
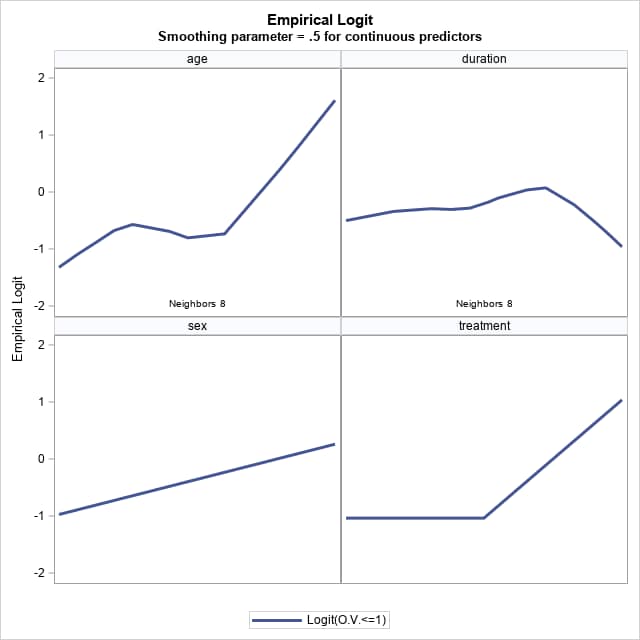
The following uses the data in the example titled "Logistic Modeling with Categorical Predictors" in the LOGISTIC documentation. The response, Pain, is binary. Four predictors are of interest, two of which, Age and Duration, are continuous with many levels. The following call of the EmpiricalLogitPlot macro plots the single logit for the event (Pain="Yes"). Since the sample size is small (N=60), a smaller number of neighbors (neighbors=8) is requested for the continuous predictors. Also, a little more smoothing of the LOESS curve is applied by smooth=.5 to the continuous predictors than is done by the default (smooth=.3).
%EmpiricalLogitPlot(data=Neuralgia, y=Pain,
x=sex age duration treatment, neighbors=8, smooth=.5)
The Response Profile table confirms that Pain="Yes", the intended event level, is associated with the first Ordered Value. Instead of the below panel of plots, individual plots for the predictors showing their levels on the horizontal axis can be drawn by specifying options=nopanel.
 |
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | z/OS | ||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | Analytics ==> Categorical Data Analysis SAS Reference ==> Procedures ==> LOGISTIC Analytics ==> Statistical Graphics SAS Reference ==> Procedures ==> GENMOD SAS Reference ==> Procedures ==> GLIMMIX SAS Reference ==> Procedures ==> PROBIT |
| Date Modified: | 2021-08-27 09:05:52 |
| Date Created: | 2009-11-20 16:41:22 |