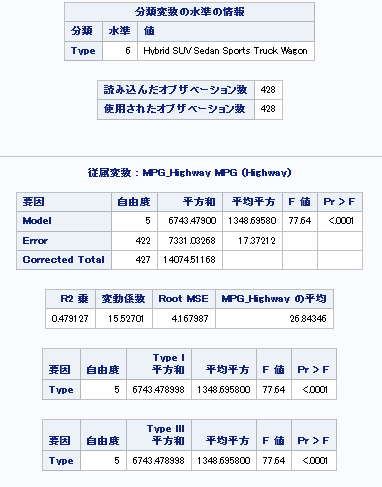
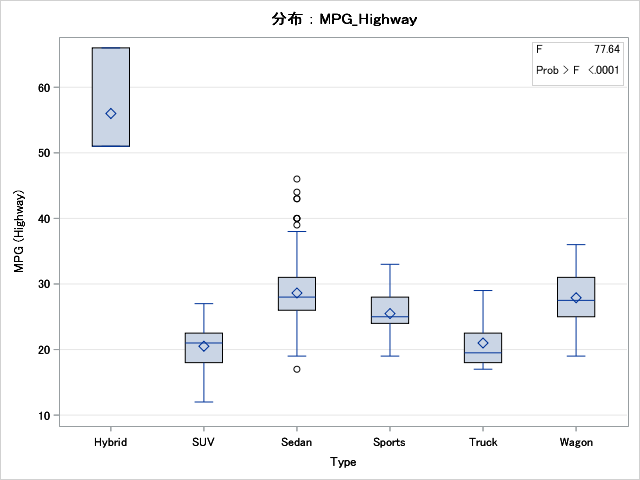
一元配置分散分析タスク
オプションの設定
|
オプション名
|
説明
|
|---|---|
|
分散の等分散性
|
|
|
検定
|
実行する検定の種類を指定します。有効な値は次のとおりです。
None
検定を実行しないことを指定します。
Bartlett
データが正規分布である場合に、Type Iの誤差率を正確に計算します。
|
|
検定(続き)
|
Brown & Forsythe
Leveneの検定の一種です。等分散を調べる際は、グループの中央値からの絶対偏差に基づいて行います。この検定は分散の差異を調べるのに適していますが、データに大きなグループが複数含まれている場合はリソースの消費量が大きくなります。
Levene
2乗残差を計算して等分散を調べます。Leveneの検定は分散の等分散性の標準検定と考えられています。これがデフォルトです。
O'Brien
O'Brienの検定(2乗残差を使用するLeveneの検定を変更したもの)を指定します。
|
|
Welch's variance-weighted ANOVA
|
重み付き分散を使用してグループの平均を検定します。等分散の仮定が満たされない場合にこの検定を使用できます。
|
|
比較
|
|
|
次の比較手法から選択できます。
Bonferroni
主効果のすべての平均値に対して平均値間の差を求めるBonferroniのt検定を実行します。
Duncanの多重比較
主効果のすべての平均値に対してDuncanの多重比較検定を実行します。
Dunnett 両側
Dunnettの両側t検定を実行して、主効果のすべての平均値について、単一の対照群と比較して、任意の処理群に有意差がないかどうかを調べます。
Dunnett左側
Dunnettの片側t検定を実行して、対照群に対して、任意の処理群が有意に小さいかを調べます。
Dunnett右側
Dunnettの片側t検定を実行して、対照群に対して、任意の処理群が有意に大きいかを調べます。
Gabriel
主効果のすべての平均値に対して、Gabrielの多重比較プロシジャを実行します。
Nelson
最小二乗平均を使用してすべての差異を分析します。
|
|
|
Ryan-Einot-Gabriel-Welsch
主効果のすべての平均値に対して、Ryan-Einot-Gabriel-Welschの多重比較検定を実行します。
Scheffé
主効果のすべての平均値に対して、Schefféの多重比較プロシジャを実行します。
Sidak
主効果のすべての平均値に対して、Sidakの不等式により調整した水準を使用して平均値間の差異を調べる、対応のあるt検定を実行します。
Student-Newman-Keuls
主効果のすべての平均値に対して、Student-Newman-Keulsの多重比較検定を実行します。
Least significant difference (LSD)
主効果のすべての平均値に対して、対応のあるt検定を実行します。セルのサイズが等しい場合、この検定は、Fisherの最小有意差検定と同等になります。
Tukey
主効果のすべての平均値に対して、Tukeyのスチューデント化範囲検定(HSD)を実行します。グループサイズが異なる場合、これはTukey-Kramer検定になります。
選択した検定の有意水準を指定することもできます。
|
|
|
ブロット
|
|
|
デフォルトでは、結果に箱ひげ図、平均値プロットおよび最小二乗平均差のプロットが含まれます。パネルに表したり個々のプロットとして表示できる診断プロットを含めることもできます。
また、これらのプロットに含める最大点数を指定することもできます。
|
|