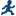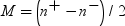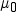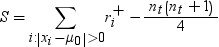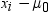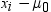T Tests Task: Paired t Test

Example: Determining the Distribution of Price – Cost

About the Paired t Test Task

A paired t test compares the mean of the differences in the observations to a given number, the null hypothesis difference. The paired t test is used when the two samples are correlated, such as two measures of blood pressure from the same person.

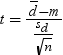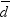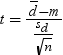To compare n paired differences to a value m, use $t equals . fraction d with macron above , minus m , over fraction s sub d , over square root of n end fraction end fraction$ , where

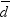is the sample mean of the paired differences and s²_d is the sample variance of the paired differences.

To run a paired t test, open the T Tests task. From the T test drop-down list, select Paired test.

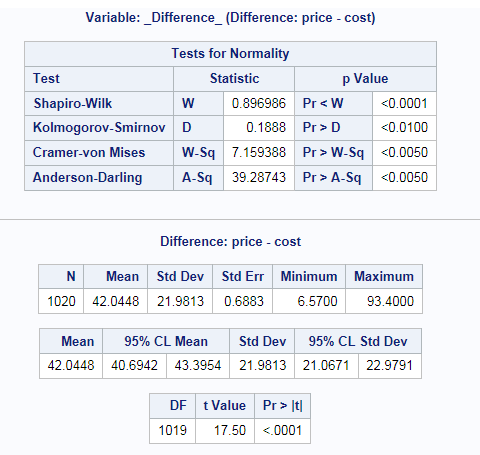
Example: Determining the Distribution of Price – Cost

In this example, you want to compare the means of differences in price and cost in the Sashelp.Pricedata data set. The null hypothesis for this test is 30.

To create this example:

In the Tasks section, expand the Statistics folder and double-click T Tests. The user interface for the T Tests task opens.
On the Data tab, select the SASHELP.PRICEDATA data set.
From the T test drop-down list, select Paired test.

Assign columns to these roles:

Role	Column Name
Group 1 variable	price
Group 2 variable	cost

On the Options tab, enter 30 in the Alternative field.
To run the task, click .

Here is a subset of the results:

The Distribution of Difference between Price and Cost

Assigning Data to Roles

To run a paired t test, select Paired test from the T test drop-down list. Assign columns to the Group 1 variable and Group 2 variable roles. The task compares these two variables. Because paired t tests are performed by subtracting each value of the Group 2 variable from the corresponding value of the Group 1 variable, the designation of the variables matters.

Setting Options

Option Name	Description
Test
Tails	specifies the number of sides (or tails) and direction of the statistical tests and test-based confidence intervals. You can choose from these options: Two-tailed test specifies two-sided tests and confidence intervals for means. Upper one-tailed test specifies upper one-sided tests in which the alternative hypothesis indicates a mean greater than the null value. The upper one-sided confidence intervals range between the lower confidence limit and infinity. Lower one-tailed test specifies lower one-sided tests in which the alternative hypothesis indicates a mean less than the null value. The lower one-sided confidence intervals range between minus infinity and the upper confidence limit.
Alternative	specifies the value of the null hypothesis.
Normality Assumption
Tests for normality	runs tests for normality that include a series of goodness-of-fit tests based on the empirical distribution function. The table provides test statistics and p-values for the Shapiro-Wilk test (provided the sample size is less than or equal to 2000), the Kolmogorov-Smirnov test, the Anderson-Darling test, and the Cramér-von Mises test.
Nonparametric Tests Note: This option is available only for a two-tailed test.
Sign test and Wilcoxon signed rank test	generates the results from these tests: The sign test statistic is , where n⁺ is the number of values that are greater than , and n^- is the number of values that are less than . Values equal to are discarded. The Wilcoxon signed rank statistic S is calculated as $s equals . sum , from , i colon vertical line , x sub i , minus , mu sub 0 , vertical line greater than 0 , to , white square , of . r with subscript i , and with superscript plus , end sub-superscript , minus . fraction n sub t , open , n sub t , plus 1 close , over 4 end fraction$ , where r⁺_i is the rank of after discarding values of and n_t is the number of x_i values not equal to . Average ranks are used for tied values.
Plots
Histogram and box plot	creates a histogram and box plot together in a single panel, sharing common X axes.
Normality plot	creates a normal quantile-quantile (Q-Q) plot.
Agreement plot	plots the second response in each pair against the first response. The mean is shown as a large bold symbol. A diagonal line with slope=0 and y-intercept=1 is overlaid. The location of the points with respect to the diagonal line reveals the strength and direction of the difference or ratio. The tighter the clustering along the same direction as the line, the stronger the positive correlation of the two measurements for each subject. Clustering along a direction perpendicular to the line indicates negative correlation.
Response profile plot	creates a plot where a line is drawn for each observation from left to right that connects the first response to the second response. The mean first response and mean second response are connected with a bold line. The more extreme the slope, the stronger the effect. A wide spread of profiles indicates high between-subject variability. Consistent positive slopes indicate strong positive correlation. Widely varying slopes indicate lack of correlation. Consistent negative slopes indicate strong negative correlation.
Confidence interval plot	creates a plot of the confidence interval for the means.