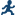Heckman's Two-Step Selection Method :: SAS(R) Studio 3.5: Task Reference Guide

About Heckman’s Two-Step Selection Method

The Heckman two-step selection method provides a means of correcting for non-randomly selected samples. It is a two-stage estimation method. The first stage performs a probit analysis on a selection equation. The second stage analyzes an outcome equation based on the first-stage binary probit model.

Example: Heckman’s Two-Step Selection Method

To create this example:

In the Tasks section, expand the Econometrics folder, and then double-click Causal Models. The user interface for the Causal Models task opens.
On the Data tab, select the SASHELP.JUNKMAIL data set.

Tip
If the data set is not available from the drop-down list, click . In the Choose a Table window, expand the library that contains the data set that you want to use. Select the data set for the example and click OK. The selected data set should now appear in the drop-down list.
Under the Analysis heading, select Heckman’s two-step selection method.

Assign columns to these roles:

Role	Column Name
Outcome Equation
Dependent variable	Business
Continuous variables	CapAvg CapTotal
Selection Equation
Dependent variable	Class
Categorical variables	Make

To run the task, click .

Here is a subset of the results:

Assigning Data to Roles

To perform an analysis that uses Heckman’s two-step selection method, you must assign an input data set. To filter the input data source, click Filter Icon

. Then under the Analysis heading, select Heckman’s two-step selection method.

You must assign columns to the Dependent variable roles for the selection and outcome equations.

Role	Description
Outcome Equation
Dependent variable	specifies a single numeric column to use.
Continuous variables	specifies the independent variables (or regressors) to use in the model for the outcome equation dependent variable.
Categorical values	specifies the independent variables to use to group the values into levels.
Include the intercept	specifies whether to include the intercept in the selection equation.
Selection Equation
Dependent variable	specifies a single numeric column that takes binary values. Select the value to use for the dependent variable from the Select samples with dependent variable drop-down list.
Continuous variables	specifies the independent variables (or regressors) to use in the model for the selection equation dependent variable.
Categorical variables	specifies the independent variables to use to group the values into levels.
Include the intercept	specifies whether to include the intercept in the selection equation.
Additional Roles
Group analysis by	enables you to obtain separate analyses of observations for each unique group.

Setting Options

Option	Description
Methods
Optimization method	specifies the iterative minimization method to use. You can use the default method, or you can choose from these methods: Conjugate-gradient Double-dogleg Nelder-Mead simplex Newton-Raphson combining line-search with ridging Quasi-Newton Trust region
Maximum number of iterations	specifies the maximum number of iterations for the selected method. You can use the default value or specify a custom value.
Variance estimation method	specifies whether to calculate the standard errors by using the corrected standard errors or the OLS standard errors.
Type of covariances of the parameter estimates	specifies the method to calculate the covariance matrix of parameter estimates. You can use the default value, or you can select the covariance from the inverse Hessian matrix, from the outer product matrix, or from the outer product and Hessian matrices (the quasi-maximum likelihood estimates).
Statistics
You can specify whether the results include the statistics that the task creates by default, the default statistics and any additional statistics that you select, or no statistics. Here is the information that you can include in the results: correlations of the parameter estimates covariances of the parameter estimates iteration history of the objective function and parameter estimates

Creating the Output Data Sets

You can create a data set that contains the parameter estimates from the analysis.