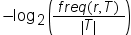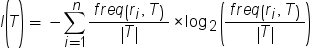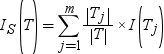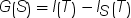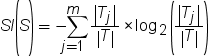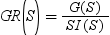Information Gain and Gain Ratio Calculations

When the Rapid growth property is enabled, node splits are determined in part by information gain ratio instead of information gain. The information gain and information gain ratio calculations and their benefits and drawbacks are explained in this section. In these explanations, an attribute is considered any specific measurement level of a classification variable or bin of a measure variable.

The information gain method chooses a split based on which attribute provides the greatest information gain. The gain is measured in bits. Although this method provides good results, it favors splitting on variables that have a large number of attributes. The information gain ratio method incorporates the value of a split to determine what proportion of the information gain is actually valuable for that split. The split with the greatest information gain ratio is chosen.

The information gain calculation starts by determining the information of the training data. The information in a response value, r, is calculated in the following expression:

T represents the training data and |T| is the number of observations. To determine the expected information of the training data, sum this expression for every possible response value:

Here, n is the total number of response values. This value is also referred to as the entropy of the training data.

Next, consider a split S on a variable X with m possible attributes. The expected information provided by that split is calculated by the following equation:

In this equation, T_j represents the observations that contain the j^th attribute.

The information gain of split S is calculated by the following equation:

Information gain ratio attempts to correct the information gain calculation by introducing a split information value. The split information is calculated by the following equation:

As its name suggests, the information gain ratio is the ratio of the information gain to the split information: