Variable Transformations

Lag Transformations

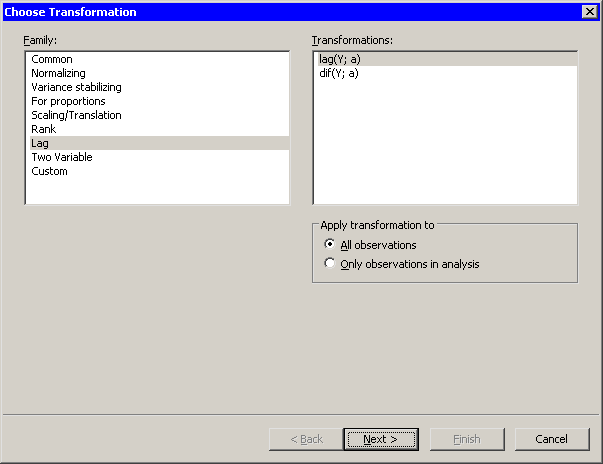
Figure 32.18 shows the transformations that are available when you select Lag from the Family list. These transformations are used to compute lagged transformations of a variable's value. Equations for these transformations are given in Table 32.7.

Figure 32.18: Lag Transformations

Table 32.7: Description of Lag Transformations

	Default	Name of
Transformation	Parameter	New Variable	Equation
lag(Y;a)		Lag_Y
dif(Y;a)		Dif_Y

The lag(Y;a) transformation creates a new variable whose th value is equal to $y_{i-a}$ for $i\gt a$ . For $i\leq a$ , the new variable contains missing values. See the documentation for the LAG function in Base SAS for further details.

The dif(Y;a) transformation creates a new variable whose th value is equal to $y_i - y_{i-a}$ for $i\gt a$ . For $i\leq a$ , the new variable contains missing values. If either or $y_{i-a}$ is missing, then so is their difference. See the documentation for the DIF function in Base SAS for further details.

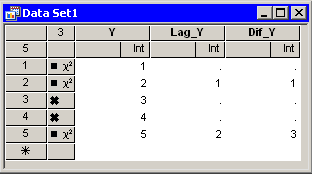
If some observations are excluded from analyses and you select Only observations in analysis, shown in Figure 32.18, then the lag transformations use only the observations included in analyses. Figure 32.19 presents an example of how these transformations behave when some observations are excluded. In the data table, Y has values 1 - 5, but observations 3 and 4 are excluded from analyses.

The Lag_Y variable is the result of the lag(Y;1) transformation. The third and fourth values are missing because these observations are excluded from analyses. The fifth value of Lag_Y is 2, the previous value of Y that is included in analyses.

The Dif_Y variable is the result of the dif(Y;1) transformation. The values are the difference between the first and second columns.

Figure 32.19: Transformations with Excluded Observations

Top of Page