Previous Page

|

Next Page

The Method Tab

You can use the Method tab to specify options for the loess algorithm.

The following options are available:

Selection method

specifies how to choose the loess smoothing parameter. This option corresponds to the SELECT= option in the MODEL statement.

AICC

selects the smoothing parameter that minimizes the corrected Akaike information criterion.

GCV

selects the smoothing parameter that minimizes the generalized cross validation criterion.

Approx. model DF

selects the smoothing parameter for which the trace of the prediction matrix is closest to the Target model DF. This corresponds to the SELECT=DF1 option in the MODEL statement.

Manual

enables you to specify the value in the Smoothing parameter field.

Exhaustive search for minimum

specifies that a global minimum be found within the range of smoothing parameter values examined. This corresponds to the GLOBAL modifier to the SELECT= option in the MODEL statement. This option is computationally expensive.

Restrict search range

specifies that only smoothing parameters greater than or equal to Lower bound and less than or equal to Upper bound be examined.

Robust reweighting iterations

specifies the number of iterative reweighting steps. Stat Studio counts the initial fit as the th reweighting iteration. This differs from the LOESS procedure, which counts the initial fit as the first iteration. Thus if you type 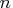in this field, the option corresponds to ITERATIONS=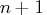 in the MODEL statement.

Interpolating polynomial

specifies whether the interpolating polynomial is linear or cubic. This corresponds to the INTERP= option in the MODEL statement.

Calculation of lookup DF

specifies the method used to calculate the "lookup" degrees of freedom used in performing statistical inference. This corresponds to the DFMETHOD= option in the MODEL statement.

Local regression polynomial

specifies the degree of the local polynomial to use for each local regression. The choice is linear or quadratic. This corresponds to the DEGREE= option in the MODEL statement.