Multivariate Analysis: Principal Component Analysis

The Tables Tab

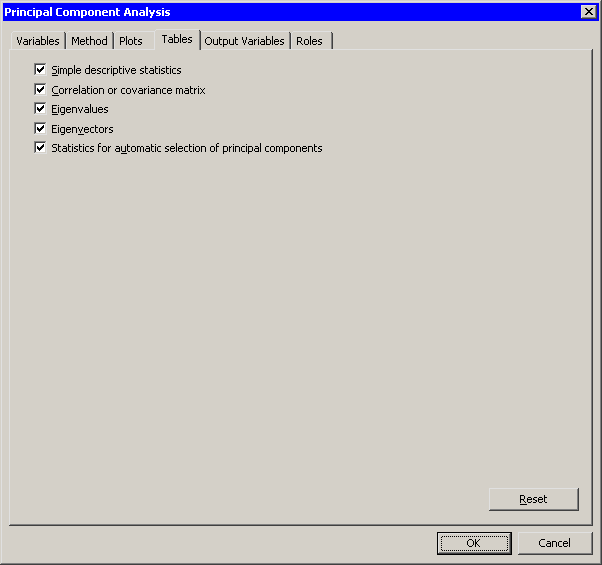
The Tables tab is shown in Figure 26.12. You can use the Tables tab to display the following tables that summarize the results of the analysis:

Simple descriptive statistics

specifies whether to display the mean and standard deviation for each variable.

Correlation or covariance matrix

specifies whether to display the correlation or covariance matrix, as selected on the Method tab.

Eigenvalues

specifies whether to display the eigenvalues of the correlation or covariance matrix, as well as the difference between successive eigenvalues, the proportion of variance explained by each eigenvalue, and the cumulative proportion of variance explained.

Eigenvectors

specifies whether to display the eigenvectors of the correlation or covariance matrix. The eigenvectors are used to form the principal components.

Statistics for automatic selection of principal components

specifies whether to display statistics that indicate how many principal components are needed to represent the 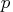-dimensional data. This table is displayed only if you request at least as many principal components as there are variables.

Figure 26.12: The Tables Tab

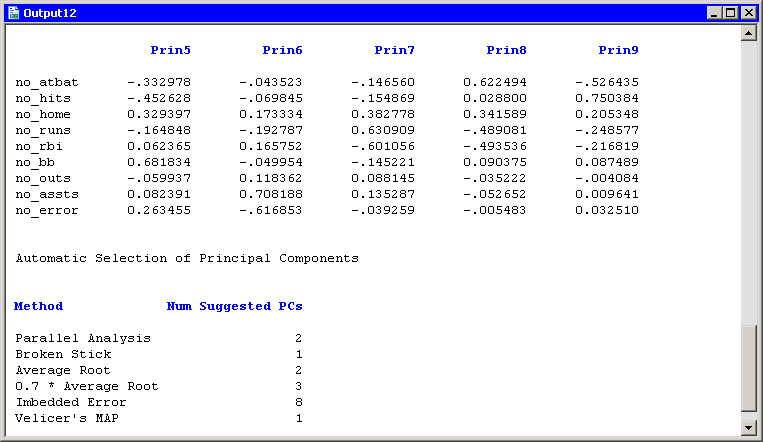
A primary use of principal component analysis is to represent -dimensional data in dimensions. In practice, it is often difficult to determine the best choice for . The "Automatic Selection of Principal Components" table, shown in Figure 26.13, is provided to help you choose . Numerous papers have been written comparing various methods for choosing , but no method has shown itself to be superior. The following list briefly describes each method reported in the table. Jackson (1991, p. 41--51) gives further details.

Parallel Analysis

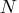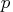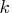generates random data sets with observations and variables. The variables are normally distributed and uncorrelated. The method chooses to be the largest integer for which the scree plot of the original data lies above the graph of the upper 95 percentiles of the eigenvalues of the random data.

Broken Stick

retains components that explain more variance than would be expected by randomly dividing the variance into 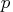parts.

Average Root

keeps components that explain more variance than the mean of the eigenvalues.

0.7 * Average Root

keeps components that explain more variance than 0.7 times the mean of the eigenvalues.

Imbedded Error

chooses 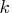to be the value that minimizes a certain function of the eigenvalues.

Velicer's MAP

chooses 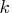to minimizes a certain function that involves partial correlations. This method is called Velicer's minimum average partial (MAP) test or Velicer's partial correlation procedure.

Figure 26.13: How Many Principal Components Are Needed?