Multivariate Analysis: Correlation Analysis

Example

In this example, you explore correlations and bivariate relationships between variables in the Hurricanes data set. The data are for North Atlantic tropical cyclones from 1988 to 2003. The data set includes information about each storm's latitude (in the latitude variable), its sustained low-level winds (wind_kts), its central atmospheric pressure (min_pressure), and the size of its eye (radius_eye). A full description of the Hurricanes data set is included in Appendix A, "Sample Data Sets."

Open the Hurricanes data set.

Select Analysis Multivariate Analysis Correlation Analysis from the main menu, as shown in Figure 25.1.

Figure 25.1: Selecting the Correlation Analysis

A dialog box appears as in Figure 25.2. You can select variables for the analysis by using the Variables tab.

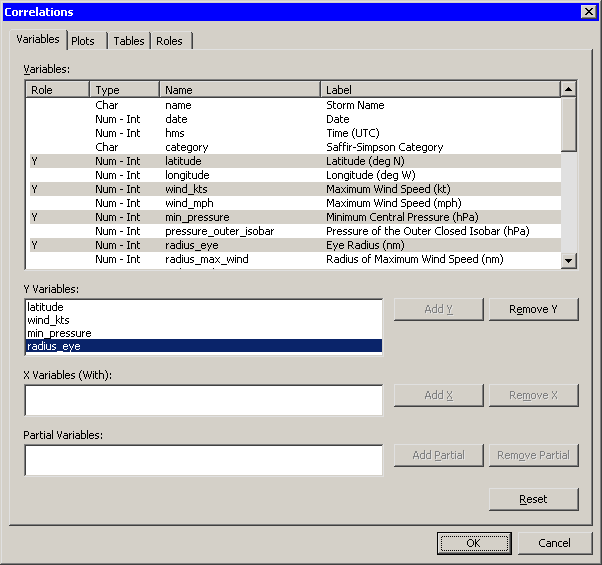
Select latitude. While holding down the CTRL key, select wind_kts, min_pressure, and radius_eye, and click Add Y.

Figure 25.2: The Variables Tab

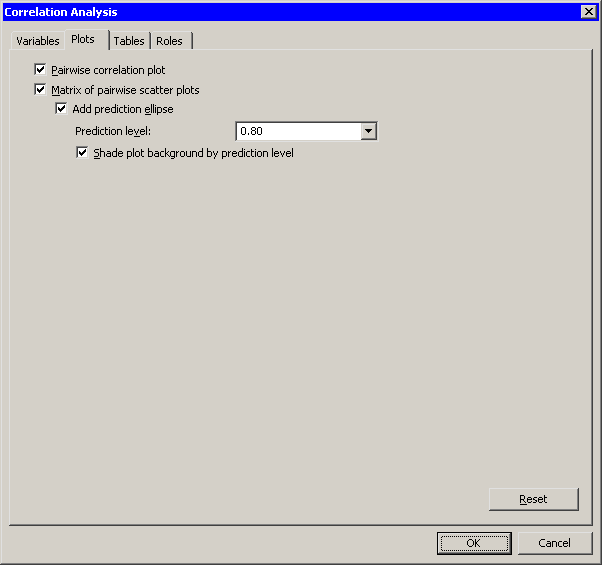
Click the Plots tab.

The Plots tab (Figure 25.3) becomes active.

Select Matrix of pairwise scatter plots.

Click OK.

Figure 25.3: The Plots Tab

The analysis calls the CORR procedure, which uses the options specified in the dialog box. The procedure displays tables in the output document, as shown in Figure 25.4. The "Simple Statistics" table (not shown in the figure) displays basic statistics such as the mean, standard deviation, and range of each variable.

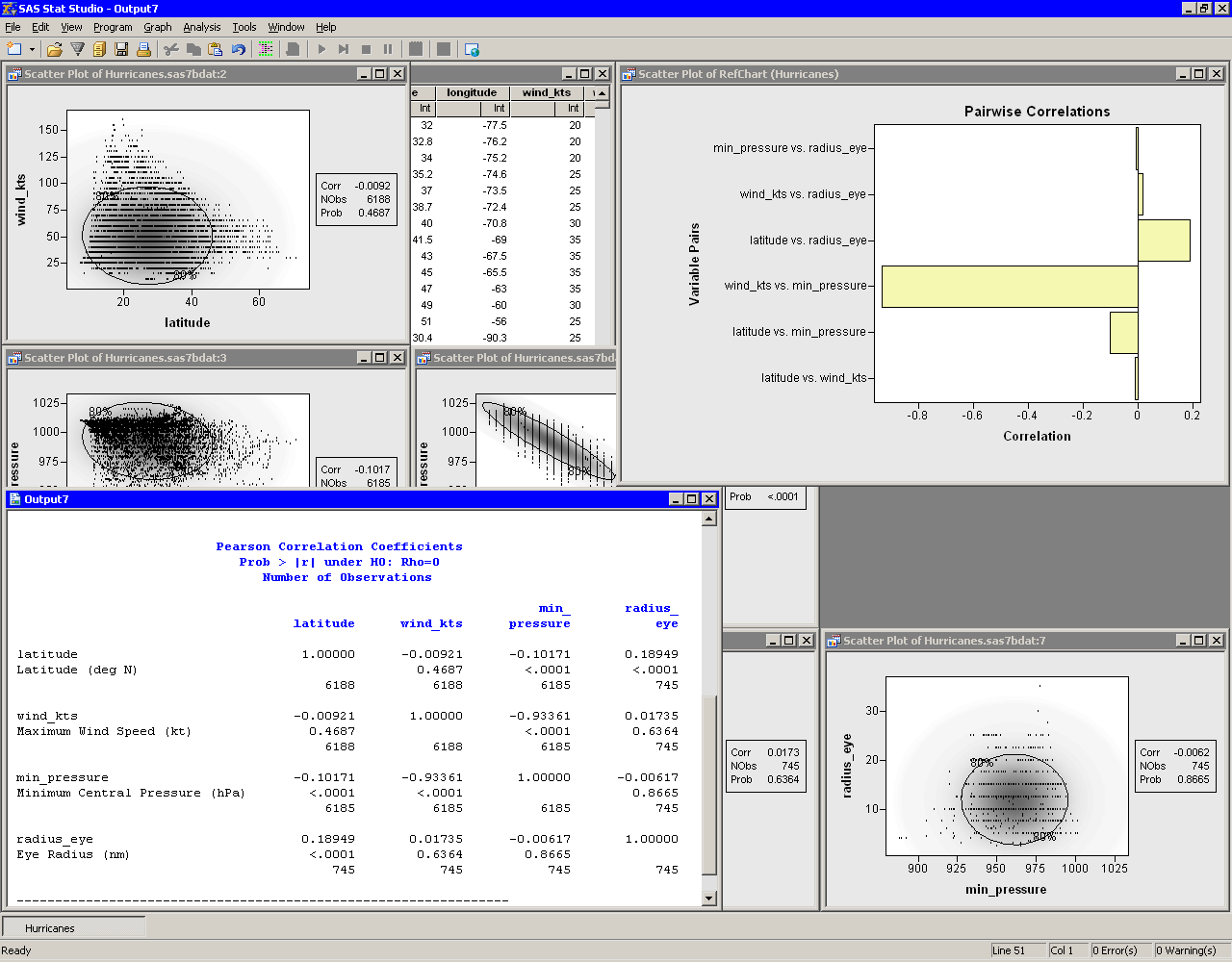
The "Pearson Correlation Coefficients" table displays the correlation coefficients between pairs of variables. In addition, the table gives the number of nonmissing observations for each pair of variables, and tests the hypothesis that the coefficient is zero.

Note that the number of observations used to compute the correlation coefficients can vary. For example, there are no missing values in the latitude of wind_kts variables, so the correlation coefficient for this pair is computed using all 6188 observations in the data set. In contrast, only 745 values for radius_eye are nonmissing, reflecting the fact that not all cyclones have well-defined eyes.

For these data, the correlation between min_pressure and wind_kts is strong and negative, with a value near -0.93. This is not surprising, since winds are determined by a pressure gradient. Although not as strong, there is also negative correlation between latitude and min_pressure. In contrast, the correlation between latitude and radius_eye is positive. The correlation between the following pairs of variables is not significantly different from zero: latitude and wind_kts, radius_eye and wind_kts, and radius_eye and min_pressure.

These results are graphically summarized in the pairwise correlations plot, shown in the upper-right corner of Figure 25.4. This plot is not linked to the original data set because it has a different number of observations. However, you can view the data table underlying this plot by pressing the F9 key when the plot is active.

Figure 25.4: Output from a Correlation Analysis

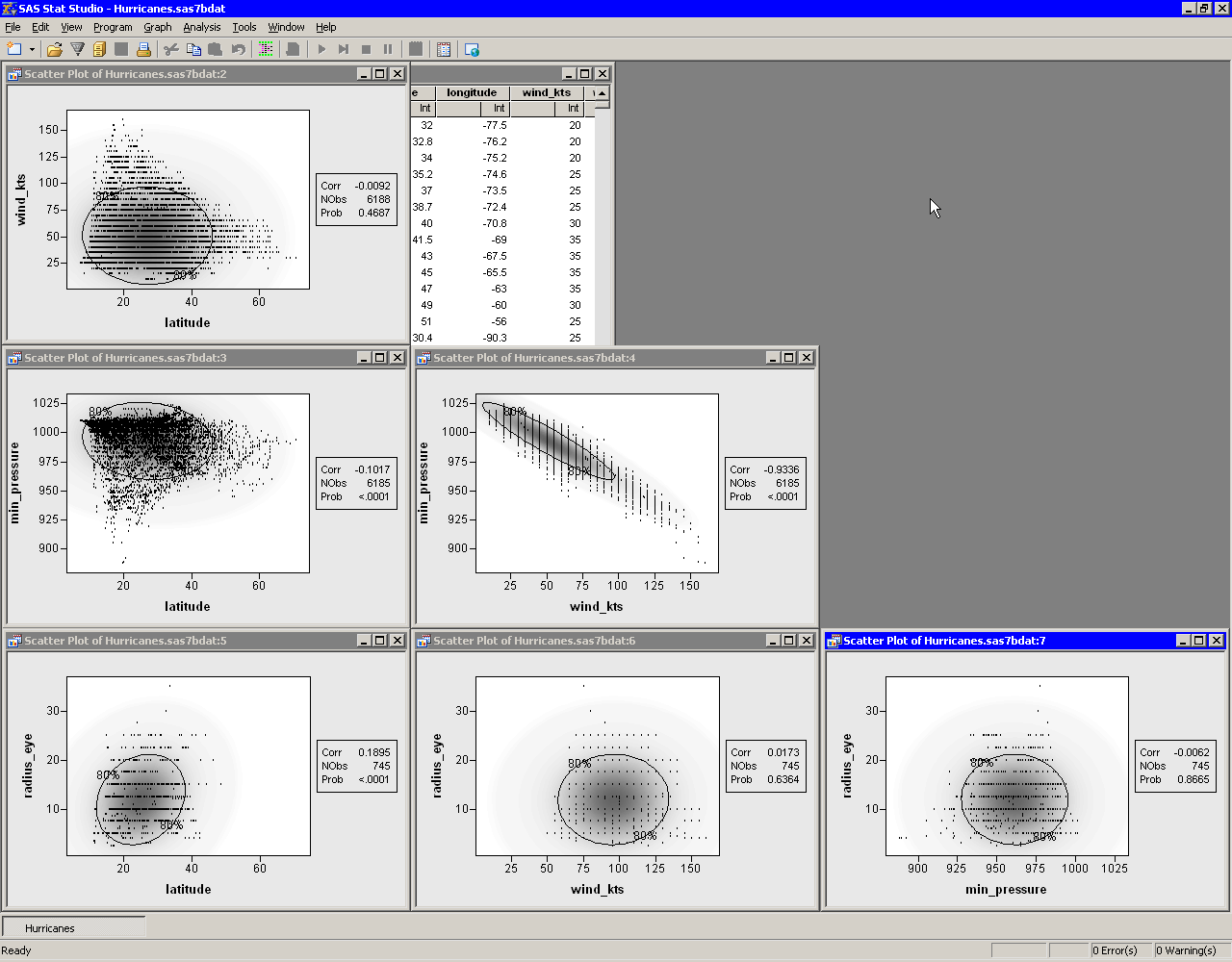
Partly visible in Figure 25.4 is the matrix of pairwise scatter plots between the variables. Some of these plots are hidden by the output window and the pairwise correlation plot. You can use the Workspace Explorer to view all the scatter plots.

Close the pairwise correlation plot.

Press ALT+X to open the Workspace Explorer.

You can use the Workspace Explorer to manage the display of plots. The Workspace Explorer is described in the section "Workspace Explorer" of Chapter 11.

Select the entry in the Workspace Explorer labeled Multivariate Correlation Analysis, as shown in Figure 25.5.

Click View.

The scatter plots associated with the analysis appear in front of other windows.

Click Close to close the Workspace Explorer.

Figure 25.5: Selecting a Group of Plots

The workspace is now arranged as shown in Figure 25.6. The ellipses show where the specified percentage of the data should lie, assuming a bivariate normal distribution. Under bivariate normality, the percentage of observations falling inside the ellipse should closely agree with the specified level. The plots also contain a gradient shading that indicates a nested sequence of ellipses. The darkest shading occurs at the bivariate means for each pair of variables. The lightest shading corresponds to 0.9999 probability.

Variables that are bivariate normal have most of their observations close to the bivariate mean and have a bivariate density that is proportional to the gradient shading. The plot of wind_kts versus latitude shows that these two variables are not bivariate normal. Similarly, min_pressure and latitude are not bivariate normal.

Figure 25.6: A Matrix of Scatter Plots

The variables wind_kts and min_pressure are highly correlated and linearly related. In contrast, wind_kts is not correlated with latitude or radius_eye, although you can still notice certain relationships:

• Cyclones with high wind speeds occur only at lower latitudes.
• Cyclones north of 43 degrees of latitude tend to have wind speeds less than 75 knots.
• The size of a cyclone's eye seems to be unrelated to the speed of its winds.

You can observe similar relationships between min_pressure and the latitude and radius_eye variables.

The matrix of scatter plots also reveals an aspect of the data that might not be apparent from univariate plots. The plots involving wind_kts and radius_eye show a granular appearance that indicates the data are rounded. Most of the wind speed measurements are rounded to the nearest five knots, whereas the values for the eye radius are rounded to the nearest 2.5 nautical miles. (You can also find observations for these variables that are not rounded.)

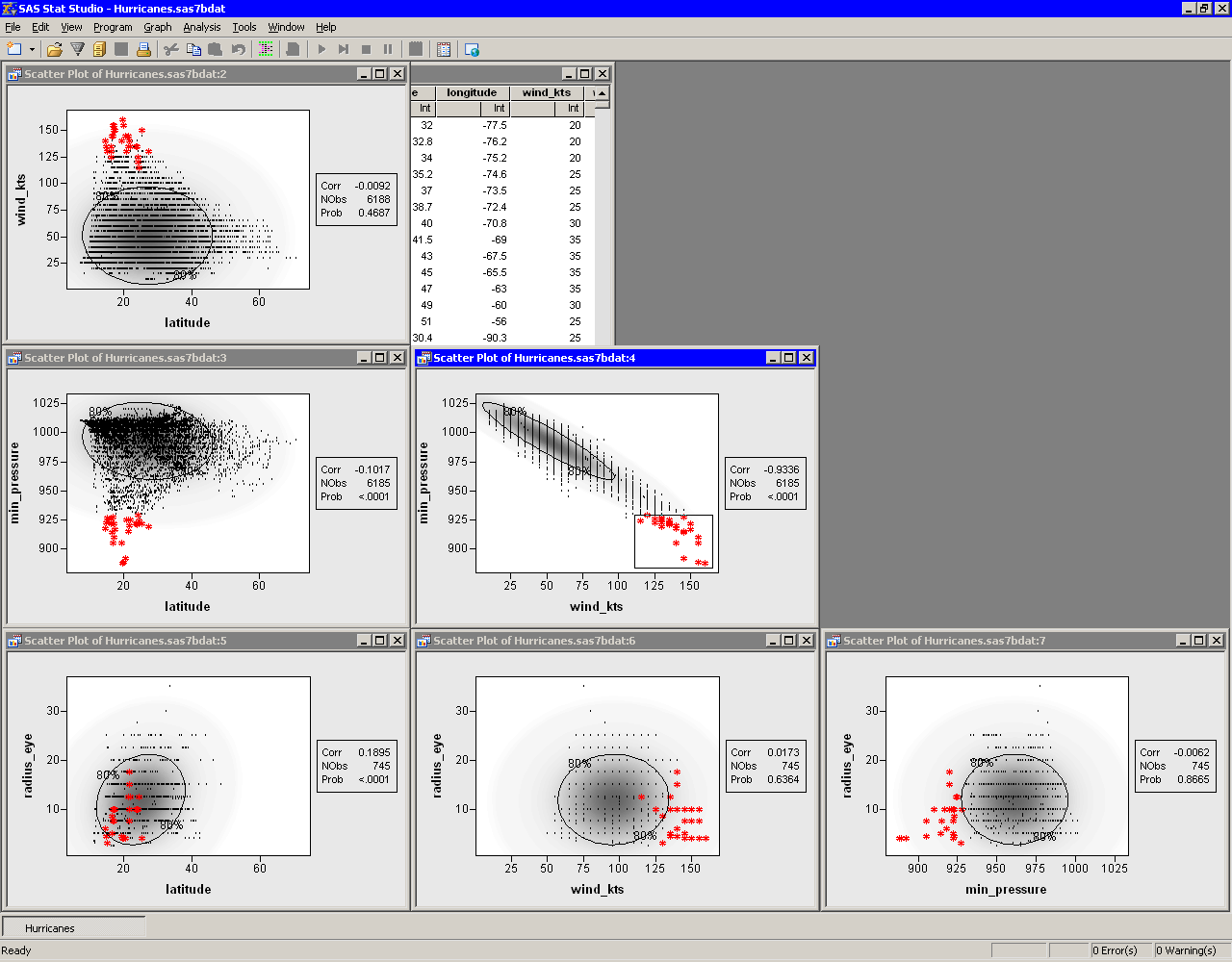
Figure 25.7 shows another use of the scatter plot matrix. Some observations with extreme values of min_pressure and wind_kts are selected. The marker shape and color for these observations were changed to make them more noticeable. You can use this technique to investigate whether outliers for one pair of variables are, in fact, multivariate outliers with respect to multivariate normality. Most of the selected data in Figure 25.7 are inside the 80% ellipse for the radius_eye versus latitude scatter plot. This indicates that these data are not far from the mean in those variables. However, a few observations (corresponding to Hurricane Hugo when it was category 5) do appear to be multivariate outliers in these variables.

Figure 25.7: Selecting Bivariate Outliers