The VARIOGRAM Procedure
Fitting with Matérn Forms
When you use a Matérn form in the fitting process, it is possible that the fitting optimizer might encounter numerical difficulties
if it tries to push the smoothing parameter  towards increasingly high values. The VARIOGRAM procedure addresses this issue by imposing an amply elevated upper bound
of 1,000,000 on the smoothness values it processes. The section Characteristics of Semivariogram Models mentions that
towards increasingly high values. The VARIOGRAM procedure addresses this issue by imposing an amply elevated upper bound
of 1,000,000 on the smoothness values it processes. The section Characteristics of Semivariogram Models mentions that 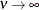 gives the Gaussian model. In the scenario of progressively increasing smoothness values, PROC VARIOGRAM acknowledges that
the Matérn form behavior tends asymptotically to become Gaussian and replaces automatically the Matérn with a Gaussian form
in the model. Subsequently, fitting resumes with the resulting model.
gives the Gaussian model. In the scenario of progressively increasing smoothness values, PROC VARIOGRAM acknowledges that
the Matérn form behavior tends asymptotically to become Gaussian and replaces automatically the Matérn with a Gaussian form
in the model. Subsequently, fitting resumes with the resulting model.
If you explore fitting of multiple models, then any duplicate models that might occur due to Matérn-to-Gaussian form conversions are fitted only once. Also, if a nested model has more than one Matérn form, then the fitting process checks one of them at a time about whether they need to be replaced by a Gaussian form. Consequently, following the switch of one Matérn form, the fitting process starts anew with the resulting model before any decisions for additional form conversions are made.
Replacement of the Matérn form with the Gaussian form occurs by default when 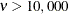 . However, you can control this threshold value with the MTOGTOL=
parameter of the MODEL
statement. Practically, the Matérn form starts to resemble the Gaussian behavior for
. However, you can control this threshold value with the MTOGTOL=
parameter of the MODEL
statement. Practically, the Matérn form starts to resemble the Gaussian behavior for  values that are about
values that are about 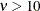 . If you encounter such conversions of the Matérn form into Gaussian and you prefer to set a lower
. If you encounter such conversions of the Matérn form into Gaussian and you prefer to set a lower  threshold for the conversion than the default, you might experience improved code performance because computation of the
Matérn semivariance can be numerically demanding.
threshold for the conversion than the default, you might experience improved code performance because computation of the
Matérn semivariance can be numerically demanding.
