The VARCLUS Procedure
Getting Started: VARCLUS Procedure
This example demonstrates how you can use PROC VARCLUS to cluster variables.
The following data are job ratings of police officers. The officers were rated by their supervisors on 13 job skills on a
scale from 1 to 9. There is also an overall rating that is not used in this analysis. The following DATA step creates the
SAS data set JobRat:
data JobRat;
input
(Communication_Skills
Problem_Solving
Learning_Ability
Judgement_under_Pressure
Observational_Skills
Willingness_to_Confront_Problems
Interest_in_People
Interpersonal_Sensitivity
Desire_for_Self_Improvement
Appearance
Dependability
Physical_Ability
Integrity
Overall_Rating)
(1.);
datalines;
26838853879867
74758876857667
56757863775875
67869777988997
99997798878888
... more lines ...
99997899799799
99899899899899
76656399567486
;
The following statements cluster the variables:
proc varclus data=JobRat maxclusters=3; var Communication_Skills--Integrity; run;
The DATA= option specifies the SAS data set JobRat as input.
The MAXCLUSTERS=3 option specifies that no more than three clusters be computed. By default, PROC VARCLUS splits and optimizes clusters until all clusters have a second eigenvalue less than one. In this example, the default setting would produce only two clusters, but going to three clusters produces a more interesting result.
The VAR statement lists the numeric variables (Communication_Skills -- Integrity) to be used in the analysis. The overall rating is omitted from the list of variables.
Although PROC VARCLUS displays output for one cluster, two clusters, and three clusters, the following figures display only the final analysis for three clusters.
For each cluster, Figure 120.1 displays the number of variables in the cluster, the cluster variation, the total explained variation, and the proportion of the total variance explained by the variables in the cluster. The variance explained by the variables in a cluster is similar to the variance explained by a factor in common factor analysis, but it includes contributions only from the variables in the cluster rather than from all variables.
The line labeled "Total variation explained" in Figure 120.1 gives the sum of the explained variation over all clusters. The final "Proportion" represents the total explained variation divided by the sum of cluster variation. This value, 0.6715, indicates that about 67% of the total variation in the data can be accounted for by the three cluster components.
Figure 120.1: Cluster Summary for Three Clusters from PROC VARCLUS
| Cluster Summary for 3 Clusters | |||||
|---|---|---|---|---|---|
| Cluster | Members | Cluster Variation |
Variation Explained |
Proportion Explained |
Second Eigenvalue |
| 1 | 6 | 6 | 3.771349 | 0.6286 | 0.7093 |
| 2 | 5 | 5 | 3.575933 | 0.7152 | 0.5035 |
| 3 | 2 | 2 | 1.382005 | 0.6910 | 0.6180 |
| Total variation explained = 8.729286 Proportion = 0.6715 |
Figure 120.2 shows how the variables are clustered. Figure 120.2 also displays the R-square value of each variable with its own cluster and the R-square value with its nearest cluster. The
R-square value for a variable with the nearest cluster should be low if the clusters are well separated. The last column displays
the ratio of 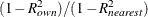 for each variable. Small values of this ratio indicate good clustering.
for each variable. Small values of this ratio indicate good clustering.
Figure 120.2: R-Square Values from PROC VARCLUS
| 3 Clusters | R-squared with | 1-R**2 Ratio |
||
|---|---|---|---|---|
| Cluster | Variable | Own Cluster |
Next Closest |
|
| Cluster 1 | Communication_Skills | 0.6403 | 0.3599 | 0.5620 |
| Problem_Solving | 0.5412 | 0.2895 | 0.6458 | |
| Learning_Ability | 0.6561 | 0.1692 | 0.4139 | |
| Observational_Skills | 0.6889 | 0.2584 | 0.4194 | |
| Willingness_to_Confront_Problems | 0.6480 | 0.3402 | 0.5335 | |
| Desire_for_Self_Improvement | 0.5968 | 0.3473 | 0.6177 | |
| Cluster 2 | Judgement_under_Pressure | 0.6263 | 0.3719 | 0.5950 |
| Interest_in_People | 0.8122 | 0.1885 | 0.2314 | |
| Interpersonal_Sensitivity | 0.7566 | 0.1387 | 0.2826 | |
| Dependability | 0.6163 | 0.4419 | 0.6875 | |
| Integrity | 0.7645 | 0.2724 | 0.3237 | |
| Cluster 3 | Appearance | 0.6910 | 0.3047 | 0.4444 |
| Physical_Ability | 0.6910 | 0.1871 | 0.3801 | |
Figure 120.3 displays the standardized scoring coefficients that are used to compute the first principal component of each cluster. Since each variable is assigned to one and only one cluster, each row of the scoring coefficients contains only one nonzero value.
Figure 120.3: Standardized Scoring Coefficients from PROC VARCLUS
| Standardized Scoring Coefficients | |||
|---|---|---|---|
| Cluster | 1 | 2 | 3 |
| Communication_Skills | 0.212170 | 0.000000 | 0.000000 |
| Problem_Solving | 0.195058 | 0.000000 | 0.000000 |
| Learning_Ability | 0.214781 | 0.000000 | 0.000000 |
| Judgement_under_Pressure | 0.000000 | 0.221313 | 0.000000 |
| Observational_Skills | 0.220086 | 0.000000 | 0.000000 |
| Willingness_to_Confront_Problems | 0.213452 | 0.000000 | 0.000000 |
| Interest_in_People | 0.000000 | 0.252025 | 0.000000 |
| Interpersonal_Sensitivity | 0.000000 | 0.243245 | 0.000000 |
| Desire_for_Self_Improvement | 0.204848 | 0.000000 | 0.000000 |
| Appearance | 0.000000 | 0.000000 | 0.601493 |
| Dependability | 0.000000 | 0.219544 | 0.000000 |
| Physical_Ability | 0.000000 | 0.000000 | 0.601493 |
| Integrity | 0.000000 | 0.244507 | 0.000000 |
Figure 120.4 displays the cluster structure and the intercluster correlations. The structure table displays the correlation of each variable with each cluster component. The table of intercorrelations contains the correlations between the cluster components.
Figure 120.4: Cluster Correlations and Intercorrelations from PROC VARCLUS
| Cluster Structure | |||
|---|---|---|---|
| Cluster | 1 | 2 | 3 |
| Communication_Skills | 0.800169 | 0.599909 | 0.427341 |
| Problem_Solving | 0.735630 | 0.538017 | 0.425463 |
| Learning_Ability | 0.810014 | 0.411316 | 0.376333 |
| Judgement_under_Pressure | 0.609876 | 0.791401 | 0.345399 |
| Observational_Skills | 0.830021 | 0.407807 | 0.508305 |
| Willingness_to_Confront_Problems | 0.805002 | 0.362927 | 0.583265 |
| Interest_in_People | 0.434138 | 0.901225 | 0.387770 |
| Interpersonal_Sensitivity | 0.372371 | 0.869826 | 0.287658 |
| Desire_for_Self_Improvement | 0.772554 | 0.589334 | 0.494842 |
| Appearance | 0.552003 | 0.393759 | 0.831266 |
| Dependability | 0.664778 | 0.785073 | 0.574460 |
| Physical_Ability | 0.432590 | 0.416070 | 0.831266 |
| Integrity | 0.521876 | 0.874342 | 0.477885 |
PROC VARCLUS next displays the summary table of statistics for the cluster history (Figure 120.5). The first three columns give the number of clusters, the total variation explained by clusters, and the proportion of variation explained by clusters, respectively.
As displayed in the first row of Figure 120.5, the variation explained by the first principal component of all the variables is 6.547402, and the proportion of variation explained is 0.5036.
When the number of clusters is two, the total variation explained is 7.96775 and the proportion of variation explained by the two clusters is 0.6129. The larger second eigenvalue of the clusters is 0.937902; so by default, PROC VARCLUS would stop splitting clusters at this point. But because the MAXCLUSTERS=3 option was specified in this example, PROC VARCLUS continues to the three-cluster solution.
When the number of clusters increases to three, the total variation explained is 8.729286 and the proportion of variation explained by the two clusters is 0.6715. The largest second eigenvalue of the clusters is 0.709323. The statistical improvement from increasing the number of clusters from two to three seems modest, but the interpretability of the three clusters argues for the three-cluster solution.
Figure 120.5 also displays the minimum proportion of variance explained by a cluster, the minimum R square for a variable, and the maximum
(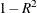 ) ratio for a variable. The last quantity is the maximum ratio of the value
) ratio for a variable. The last quantity is the maximum ratio of the value 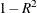 for a variable’s own cluster to the value
for a variable’s own cluster to the value 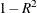 for its nearest cluster.
for its nearest cluster.
Figure 120.5: Final Cluster Summary Table from PROC VARCLUS
| Number of Clusters |
Total Variation Explained by Clusters |
Proportion of Variation Explained by Clusters |
Minimum Proportion Explained by a Cluster |
Maximum Second Eigenvalue in a Cluster |
Minimum R-squared for a Variable |
Maximum 1-R**2 Ratio for a Variable |
|---|---|---|---|---|---|---|
| 1 | 6.547402 | 0.5036 | 0.5036 | 1.772715 | 0.2995 | |
| 2 | 7.967753 | 0.6129 | 0.5475 | 0.937902 | 0.3123 | 0.8026 |
| 3 | 8.729286 | 0.6715 | 0.6286 | 0.709323 | 0.5412 | 0.6875 |
