The TTEST Procedure
TOST Equivalence Test
The hypotheses for an equivalence test are
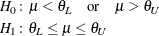
where 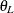 and
and 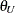 are the lower and upper bounds specified in the TOST
option in the PROC TTEST
statement, and
are the lower and upper bounds specified in the TOST
option in the PROC TTEST
statement, and 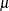 is the analysis criterion (mean, mean ratio, or mean difference, depending on the analysis). Following the two one-sided
tests (TOST) procedure of Schuirmann (1987), the equivalence test is conducted by performing two separate tests:
is the analysis criterion (mean, mean ratio, or mean difference, depending on the analysis). Following the two one-sided
tests (TOST) procedure of Schuirmann (1987), the equivalence test is conducted by performing two separate tests:
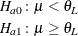
and
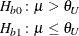
The overall p-value is the larger of the two p-values of those tests.
Rejection of 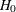 in favor of
in favor of 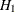 at significance level
at significance level  occurs if and only if the 100(1 – 2
occurs if and only if the 100(1 – 2  )% confidence interval for
)% confidence interval for 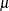 is contained completely within
is contained completely within 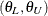 . So, the 100(1 – 2
. So, the 100(1 – 2  )% confidence interval for
)% confidence interval for 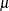 is displayed in addition to the usual 100(1 –
is displayed in addition to the usual 100(1 –  )% interval.
)% interval.
For further discussion of equivalence testing for the designs supported in the TTEST procedure, see Phillips (1990); Diletti, Hauschke, and Steinijans (1991); Hauschke et al. (1999).
