The TTEST Procedure
AB/BA Crossover Design
Let "A" and "B" denote the two treatment values. Define the following notation:

So 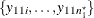 and
and 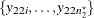 are all observed at treatment level A, and
are all observed at treatment level A, and 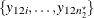 and
and 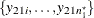 are all observed at treatment level B.
are all observed at treatment level B.
Define the period difference for an observation as the difference between period 1 and period 2 response values:
![\[ \mr{pd}_{kji} = y_{k1i} - y_{k2i} \]](images/statug_ttest0148.png)
for 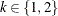 and
and 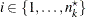 . Similarly, the period ratio is the ratio between period 1 and period 2 response values:
. Similarly, the period ratio is the ratio between period 1 and period 2 response values:
![\[ \mr{pr}_{kji} = y_{k1i} / y_{k2i} \]](images/statug_ttest0151.png)
The crossover difference for an observation is the difference between treatment A and treatment B response values:
![\[ \mr{cd}_{kji} = \left\{ \begin{array}{ll} y_{k1i} - y_{k2i} \; \; , & k=1 \\ y_{k2i} - y_{k1i} \; \; , & k=2 \\ \end{array} \right. \]](images/statug_ttest0152.png)
Similarly, the crossover ratio is the ratio between treatment A and treatment B response values:
![\[ \mr{cr}_{kji} = \left\{ \begin{array}{ll} y_{k1i} / y_{k2i} \; \; , & k=1 \\ y_{k2i} / y_{k1i} \; \; , & k=2 \\ \end{array} \right. \]](images/statug_ttest0153.png)
In the absence of the IGNOREPERIOD
option in the PROC TTEST
statement, the data are split into two groups according to treatment sequence and analyzed as a two-independent-sample design.
If DIST=
NORMAL, then the analysis of the treatment effect is based on the half period differences 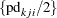 , and the analysis for the period effect is based on the half crossover differences
, and the analysis for the period effect is based on the half crossover differences 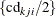 . The computations for the normal difference analysis are the same as in the section Normal Difference (DIST=NORMAL TEST=DIFF) for the two-independent-sample design. The normal ratio analysis without the IGNOREPERIOD
option is not supported for the AB/BA crossover design. If DIST=
LOGNORMAL, then the analysis of the treatment effect is based on the square root of the period ratios
. The computations for the normal difference analysis are the same as in the section Normal Difference (DIST=NORMAL TEST=DIFF) for the two-independent-sample design. The normal ratio analysis without the IGNOREPERIOD
option is not supported for the AB/BA crossover design. If DIST=
LOGNORMAL, then the analysis of the treatment effect is based on the square root of the period ratios 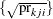 , and the analysis for the period effect is based on the square root of the crossover ratios
, and the analysis for the period effect is based on the square root of the crossover ratios 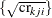 . The computations are the same as in the section Lognormal Ratio (DIST=LOGNORMAL TEST=RATIO) for the two-independent-sample design.
. The computations are the same as in the section Lognormal Ratio (DIST=LOGNORMAL TEST=RATIO) for the two-independent-sample design.
If the IGNOREPERIOD
option is specified, then the treatment effect is analyzed as a paired analysis on the (treatment A, treatment B) response
value pairs, regardless of treatment sequence. So the set of pairs is taken to be the concatenation of 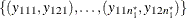 and
and 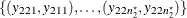 . The computations are the same as in the section Paired Design.
. The computations are the same as in the section Paired Design.
See Senn (2002, Chapter 3) for a more detailed discussion of the AB/BA crossover design.
