The TREE Procedure

The TREE procedure creates tree diagrams from a SAS data set that contains the tree structure. You can create this type of data set with the CLUSTER or VARCLUS procedure. See Chapter 33: The CLUSTER Procedure, and Chapter 120: The VARCLUS Procedure, for more information.

In the following example, the VARCLUS procedure is used to divide a set of variables into hierarchical clusters and to create the SAS data set that contains the tree structure. The TREE procedure then generates the tree diagrams.

The following data, from Hand et al. (1994), represent the amount of protein consumed from nine food groups for each of 25 European countries. The nine food groups are red meat (RedMeat), white meat (WhiteMeat), eggs (Eggs), milk (Milk), fish (Fish), cereal (Cereal), starch (Starch), nuts (Nuts), and fruits and vegetables (FruVeg).

The following SAS statements create the data set Protein:

data Protein;                                                        
   input Country $15. RedMeat WhiteMeat Eggs Milk
      Fish Cereal Starch Nuts FruVeg;
   datalines;
Albania        10.1  1.4  0.5   8.9  0.2  42.3  0.6  5.5  1.7
Austria         8.9 14.0  4.3  19.9  2.1  28.0  3.6  1.3  4.3   
Belgium        13.5  9.3  4.1  17.5  4.5  26.6  5.7  2.1  4.0
Bulgaria        7.8  6.0  1.6   8.3  1.2  56.7  1.1  3.7  4.2
Czechoslovakia  9.7 11.4  2.8  12.5  2.0  34.3  5.0  1.1  4.0
Denmark        10.6 10.8  3.7  25.0  9.9  21.9  4.8  0.7  2.4
E Germany       8.4 11.6  3.7  11.1  5.4  24.6  6.5  0.8  3.6
Finland         9.5  4.9  2.7  33.7  5.8  26.3  5.1  1.0  1.4
France         18.0  9.9  3.3  19.5  5.7  28.1  4.8  2.4  6.5
Greece         10.2  3.0  2.8  17.6  5.9  41.7  2.2  7.8  6.5
Hungary         5.3 12.4  2.9   9.7  0.3  40.1  4.0  5.4  4.2
Ireland        13.9 10.0  4.7  25.8  2.2  24.0  6.2  1.6  2.9
Italy           9.0  5.1  2.9  13.7  3.4  36.8  2.1  4.3  6.7
Netherlands     9.5 13.6  3.6  23.4  2.5  22.4  4.2  1.8  3.7
Norway          9.4  4.7  2.7  23.3  9.7  23.0  4.6  1.6  2.7
Poland          6.9 10.2  2.7  19.3  3.0  36.1  5.9  2.0  6.6
Portugal        6.2  3.7  1.1   4.9 14.2  27.0  5.9  4.7  7.9
Romania         6.2  6.3  1.5  11.1  1.0  49.6  3.1  5.3  2.8
Spain           7.1  3.4  3.1   8.6  7.0  29.2  5.7  5.9  7.2
Sweden          9.9  7.8  3.5   4.7  7.5  19.5  3.7  1.4  2.0
Switzerland    13.1 10.1  3.1  23.8  2.3  25.6  2.8  2.4  4.9
UK             17.4  5.7  4.7  20.6  4.3  24.3  4.7  3.4  3.3
USSR            9.3  4.6  2.1  16.6  3.0  43.6  6.4  3.4  2.9
W Germany      11.4 12.5  4.1  18.8  3.4  18.6  5.2  1.5  3.8
Yugoslavia      4.4  5.0  1.2   9.5  0.6  55.9  3.0  5.7  3.2
;                                                            

The data set Protein contains the character variable Country and the nine numeric variables that represent the food groups. The $15. in the INPUT statement specifies that the variable Country is a character variable with a length of 15.

The following statements cluster the variables in the data set Protein:

ods graphics on;

proc varclus data=Protein outtree=Tree centroid maxclusters=4
             plots=dendrogram(vertical height=ncl);
   var RedMeat--FruVeg;
run;

The OUTTREE= option creates an output data set named Tree to contain the tree structure. The CENTROID option specifies the centroid clustering method, and the MAXCLUSTERS= option specifies that the largest number of clusters desired is four. The VAR statement specifies that all numeric variables (RedMeat—FruVeg) are used by the procedure. Since ODS Graphics is enabled, PROC VARCLUS creates a dendrogram, which is displayed in Figure 118.1. The option plots=dendrogram(vertical height=ncl) specifies a vertical dendrogram with the number of clusters on the vertical axis. The default is a horizontal dendrogram with, for this cluster analysis, the proportion of variance explained on the horizontal axis.

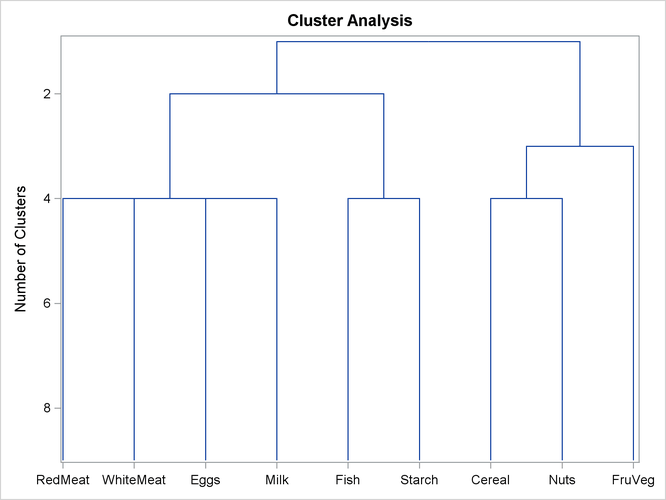
The output data set Tree, created by the OUTTREE= option in the previous statements, contains the following variables:

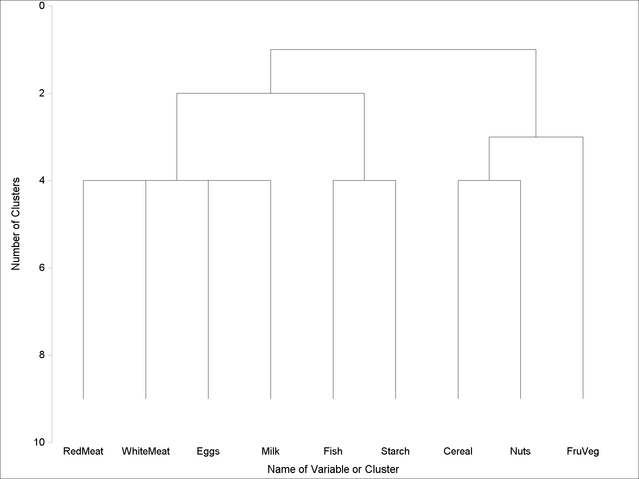
The following statements use PROC TREE to a produce tree diagram of the clusters created by PROC VARCLUS:

proc tree data=tree vaxis=axis1;
   axis1 label=(angle=90);
run;

The AXIS1 statement rotates the Y-axis label so that it is displayed in the same way as in the dendrogram from PROC VARCLUS. Figure 118.2 displays the tree diagram.

In each diagram, the name of the cluster is displayed on the horizontal axis and the number of clusters is displayed on the vertical (height) axis.

As you look up from the bottom of either diagram, clusters are progressively joined until a single, all-encompassing cluster is formed at the top (or root) of the tree. Clusters exist at each level of the diagram. For example, at the level where the diagram indicates three clusters, the clusters are as follows:

As you proceed up the diagram one level, the number of clusters is two:

The following statements illustrate how you can specify the numeric variable that defines the height of each node (cluster) in the tree:

proc tree data=Tree horizontal haxis=axis1;
   axis1 order=(0 to 1 by 0.2);
   height _PROPOR_;
   label _name_ = 'Variable';
run;

The HORIZONTAL option in the PROC TREE statement orients the tree diagram horizontally. The HAXIS= option specifies that the AXIS1 statement be used to customize the appearance of the horizontal axis. The ORDER= option in the AXIS1 statement (see SAS/GRAPH: Reference) specifies the data values in the order in which they are to appear on the axis. The HEIGHT statement specifies the variable _PROPOR_ (the proportion of variance explained) as the height variable. The LABEL statement supplies a short Y-axis label.

The resulting tree diagram is shown in Figure 118.3.

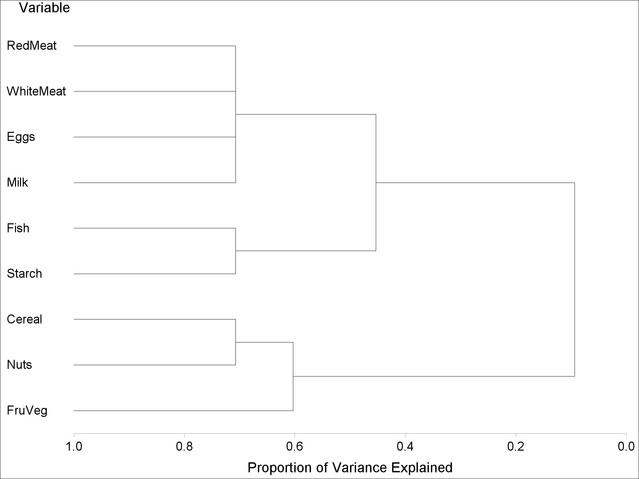
As you look from left to right in the diagram, objects and clusters are progressively joined until a single, all-encompassing cluster is formed at the right (or root) of the tree.

Clusters exist at each level of the diagram, represented by horizontal line segments. Each vertical line segment represents a point where leaves and branches are connected into progressively larger clusters.

For example, three clusters are formed at the leftmost point along the axis where three horizontal line segments exist. At that point, where a vertical line segment connects the Cereal-Nuts and FruVeg clusters, the proportion of variance explained is about 0.6 (_PROPOR_ = 0.6). At the next clustering level the variables Fish and Starch are clustered with variables RedMeat through Milk, resulting in a total of two clusters. The proportion of variance explained is about 0.45 at that point.