The SURVEYSELECT Procedure

Poisson Sampling

Poisson sampling, which you request by specifying the METHOD=POISSON option, is an unequal probability sampling method for which the total sample size is not fixed. A generalization of Bernoulli sampling, Poisson sampling also consists of independent random selection trials for the N sampling units in the input data set, but the sampling units can have different inclusion probabilities. You provide inclusion probabilities for Poisson sampling in the variable that you specify in the SIZE statement.

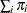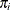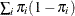The expected value of the sample size for Poisson sampling is $\sum _ i { \pi _ i }$ , where $\pi _ i$ is the inclusion probability for sampling unit i. The variance of the sample size is $\sum _ i { \pi _ i ( 1 - \pi _ i ) }$ .

For Poisson sampling, the selection probability for unit i is the inclusion probability 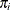$\pi _ i$ that you specify by using the SIZE statement. PROC SURVEYSELECT computes the sampling weight for unit i as the inverse of the selection probability, which is 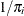$1 / \pi _ i$ . The joint selection probability for any two distinct units i and j is 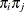$\pi _ i \pi _ j$ . For more information, see Särndal, Swensson, and Wretman (1992).