The SURVEYFREQ Procedure

Wald Log-Linear Chi-Square Test

If you specify the WLLCHISQ option in the TABLES statement, PROC SURVEYFREQ computes a Wald test for independence based on the log odds ratios. For more information about Wald tests, see the section Wald Chi-Square Test.

For a two-way table of R rows and C columns, the Wald log-linear test is based on the (R – 1)(C – 1)-dimensional array of elements 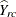$\widehat{Y}_{rc}$,

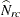\[ \widehat{Y}_{rc} = \log \widehat{N}_{rc} ~ - ~ \log \widehat{N}_{rC} ~ - ~ \log \widehat{N}_{Rc} ~ + ~ \log \widehat{N}_{RC} \]

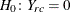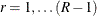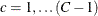where $\widehat{N}_{rc}$ is the estimated total for table cell (r, c). The null hypothesis of independence between the row and column variables can be expressed as $ H_0\colon Y_{rc} = 0$ for all $r = 1, \ldots (R-1)$ and $c=1, \ldots (C-1)$. This null hypothesis can be stated equivalently in terms of cell proportions.

The generalized Wald log-linear chi-square statistic is computed as

\[ Q_\mi {L} = \widehat{\mb{Y}}’ ~ \widehat{\mb{V}}(\widehat{\mb{Y}})^{-1} ~ \widehat{\mb{Y}} \]

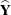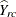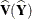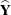where $\widehat{\mb{Y}}$ is the (R – 1)(C – 1)-dimensional array of the $\widehat{Y}_{rc}$, and $\widehat{\mb{V}}(\widehat{\mb{Y}})$ estimates the variance of $\widehat{\mb{Y}}$,

\[ \widehat{\mb{V}}(\widehat{\mb{Y}}) = \mb{A} ~ \mb{D}^{-1} ~ \widehat{V}(\widehat{\mb{N}}) ~ \mb{D}^{-1} ~ \mb{A}’ \]

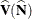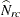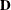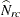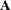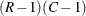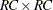where $\widehat{\mb{V}}(\widehat{\mb{N}})$ is the covariance matrix of the estimates $\widehat{N}_{rc}$, which is computed as described in the section Covariances of Frequency Estimates. $\mb{D}$ is a diagonal matrix with the estimated totals $\widehat{N}_{rc}$ on the diagonal, and $\mb{A}$ is the $(R-1)(C-1)$ by $RC \times RC$ linear contrast matrix.

Under the null hypothesis of independence, the statistic 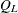$Q_\mi {L}$ approximately follows a chi-square distribution with (R – 1)(C – 1) degrees of freedom for large samples.

PROC SURVEYFREQ computes the Wald log-linear F statistic as

\[ F_\mi {L} = Q_\mi {L} ~ / ~ (R-1)(C-1) \]

Under the null hypothesis of independence, 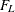$F_\mi {L}$ approximately follows an F distribution with (R – 1)(C – 1) numerator degrees of freedom. PROC SURVEYFREQ computes the denominator degrees of freedom as described in the section Degrees of Freedom. Alternatively, you can use the DF= option in the TABLES statement to specify the denominator degrees of freedom.

For tables larger than 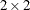$2 \times 2$, PROC SURVEYFREQ also computes the adjusted Wald log-linear F statistic as

\[ F_{\mathit{Adj\_ L}} = Q_\mi {L} ~ (s - k + 1) ~ / ~ (k s) \]

where k = (R – 1)(C – 1), and s is the denominator degrees of freedom, which is computed as described in the section Degrees of Freedom. Alternatively, you can use the DF= option in the TABLES statement to specify the value of s. For 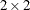$2 \times 2$ tables, k = (R – 1)(C – 1) = 1, and therefore the adjusted Wald F statistic equals the (unadjusted) Wald F statistic and has the same numerator and denominator degrees of freedom.

Under the null hypothesis, 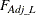$F_{\mathit{Adj\_ L}}$ approximately follows an F distribution with k numerator degrees of freedom and (s – k + 1) denominator degrees of freedom.