The SIMNORMAL Procedure

Unconditional Simulation

It is a simple matter to produce an 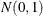$N(0,1)$ random number, and by stacking k such numbers in a column vector you obtain a vector with independent standard normal components 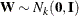$\bW \sim N_ k(\mb{0},\bI )$ . The meaning of the terms independence and randomness in the context of a deterministic algorithm required for the generation of these numbers is somewhat subtle; see Knuth (1973, Vol. 2, Chapter 3) for a discussion of these issues.

Rather than 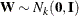$\bW \sim N_ k(\mb{0},\bI )$ , what is required is the generation of a vector 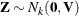$\bZ \sim N_ k(\mb{0},\bV )$ —that is,

$\bZ = \left[ \begin{array}{c} Z_1\\ Z_2\\ \vdots \\ Z_ k \end{array} \right]$

with covariance matrix

$\bV = \left( \begin{array}{cccc} \sigma _{11} & \sigma _{12} & \cdots & \sigma _{1k}\\ \sigma _{21} & \sigma _{22} & \cdots & \sigma _{2k}\\ & \ddots & & \\ \sigma _{k1} & \sigma _{k2} & \cdots & \sigma _{kk} \end{array} \right)$

where

$\sigma _{ij} = \mbox{Cov}(Z_ i,Z_ j)$

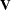If the covariance matrix is symmetric and positive definite, it has a Cholesky root $\bL$ such that $\bV$ can be factored as

$\bV =\bL \bL ’$

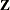where $\bL$ is lower triangular. See Ralston and Rabinowitz (1978, Chapter 9, Section 3-3) for details. This vector $\bZ$ can be generated by the transformation 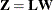$\bZ =\bL \bW$ . Note that this is where the assumption of multivariate normality is crucial. If 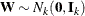$\bW \sim N_ k(\mb{0},\bI _ k)$ , then 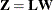$\bZ =\bL \bW$ is also normal or Gaussian. The mean of Z is

$\mr{E}(\bZ ) = \bL (\mr{E}(\bW )) = 0$

and the variance is

$\mr{Var}(\bZ ) = \mr{Var}(\bL \bW ) = \mr{E}(\bL \bW \bW ’\bL ’) = \bL ~ \mr{E}(\bW \bW ’)~ \bL ’ = \bL \bL ’ = \bV$

Finally, let 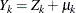$Y_ k = Z_ k + \mu _ k$ ; that is, you add a mean term to each variable 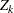$Z_ k$ . The covariance structure of the 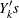$Y_ k’s$ remains the same. Unconditional simulation is done by simply repeatedly generating k 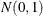$N(0,1)$ random numbers, stacking them, and performing the transformation

$\bW \longmapsto \bZ = \bL \bW \longmapsto \bY = \bZ + \bmu$