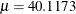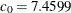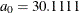The SIM2D Procedure

Preliminary Spatial Data Analysis

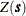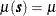A semivariance analysis of the coal seam thickness thick data set is performed in Getting Started: VARIOGRAM Procedure in Chapter 122: The VARIOGRAM Procedure. The analysis considers the spatial random field (SRF) $Z(\bm {s})$ of the Thick variable to be free of surface trends. The expected value $E[Z(\bm {s})]$ is then a constant $\mu (\bm {s}) = \mu $, which suggests that you can work with the original thickness data rather than residuals from a trend surface fit. In fact, a reasonable approximation of the spatial process generating the coal seam data is given by

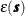\[ Z(\bm {s}) = \mu + \varepsilon (\bm {s}) \]

where $\varepsilon (\bm {s})$ is a Gaussian SRF with Gaussian covariance structure

\[ C_ z(\bm {h}) = c_0\exp \left(-\frac{h^2}{a_0^2}\right) \]

Of note, the term "Gaussian" is used in two ways in this description. For a set of locations 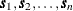$\bm {s}_1,\bm {s}_2,\ldots ,\bm {s}_ n$, the random vector

\[ \bm {Z}(\bm {s}) = \left[ \begin{array}{c} Z(\bm {s}_1) \\ Z(\bm {s}_2) \\ \vdots \\ Z(\bm {s}_ n) \\ \end{array} \right] \]

has a multivariate Gaussian or normal distribution 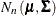$N_ n\left(\bmu , \bSigma \right)$. The (i,j) element of 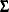$\bSigma $ is computed by 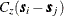$C_ z(\bm {s}_ i-\bm {s}_ j)$, which happens to be a Gaussian functional form.

Any functional form for 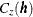$C_ z(\bm {h})$ that yields a valid covariance matrix 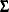$\bSigma $ can be used. Both the functional form of 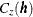$C_ z(\bm {h})$ and the parameter values

  1. $\mu =40.1173$

  2. $c_0=7.4599$

  3. $a_0=30.1111$

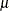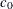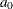are estimated by using PROC VARIOGRAM in section Theoretical Semivariogram Model Fitting in Chapter 122: The VARIOGRAM Procedure. Specifically, the expected value $\mu $ is reported in the VARIOGRAM procedure OUTV output data set, and the parameters $c_0$ and $a_0$ are estimates derived from a weighted least squares fit.

The choice of a Gaussian functional form for 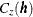$C_ z(\bm {h})$ is simply based on the data, and it is not at all crucial to the simulation. However, it is crucial to the simulation method used in PROC SIM2D that 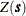$Z(\bm {s})$ be a Gaussian SRF. For details, see the section Computational and Theoretical Details of Spatial Simulation.