The SIM2D Procedure
Theoretical Development
It is a simple matter to produce an 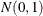 random number, and by stacking k
random number, and by stacking k 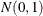 random numbers in a column vector, you can obtain a vector with independent standard normal components
random numbers in a column vector, you can obtain a vector with independent standard normal components 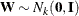 . The meaning of the terms independence and randomness in the context of a deterministic algorithm required for the generation of these numbers is subtle; see Knuth (1981, Chapter 3) for details.
. The meaning of the terms independence and randomness in the context of a deterministic algorithm required for the generation of these numbers is subtle; see Knuth (1981, Chapter 3) for details.
Rather than 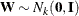 , what is required is the generation of a vector
, what is required is the generation of a vector 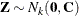 —that is,
—that is,
![\[ \mb{Z} = \left[ \begin{array}{c} Z_1\\ Z_2\\ \vdots \\ Z_ k \end{array} \right] \]](images/statug_sim2d0081.png)
with covariance matrix
![\[ \mb{C} = \left( \begin{array}{cccc} C_{11} & C_{12} & \cdots & C_{1k}\\ C_{21} & C_{22} & \cdots & C_{2k}\\ & \ddots & & \\ C_{k1} & C_{k2} & \cdots & C_{kk} \end{array} \right) \]](images/statug_sim2d0082.png)
If the covariance matrix is symmetric and positive definite, it has a
Cholesky root  such that
such that 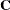 can be factored as
can be factored as
![\[ \mb{C}=\mb{LL}’ \]](images/statug_sim2d0084.png)
where  is lower triangular. See Ralston and Rabinowitz (1978, Chapter 9, Section 3-3) for details. This vector
is lower triangular. See Ralston and Rabinowitz (1978, Chapter 9, Section 3-3) for details. This vector 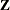 can be generated by the transformation
can be generated by the transformation 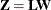 . Here is where the assumption of a Gaussian SRF is crucial. When
. Here is where the assumption of a Gaussian SRF is crucial. When 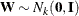 , then
, then 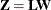 is also Gaussian. The mean of
is also Gaussian. The mean of 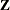 is
is
![\[ E(\mb{Z}) = \mb{L}(E(\mb{W})) = \Strong{0} \]](images/statug_sim2d0087.png)
and the variance is
![\[ \mbox{Var}(\mb{Z}) = \mbox{Var}(\mb{LW}) = E(\mb{LWW}’\mb{L}’) = \mb{L}E(\mb{WW}’)\mb{L}’ = \mb{LL}’ = \mb{C} \]](images/statug_sim2d0088.png)
Consider now an SRF 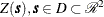 , with spatial covariance function
, with spatial covariance function 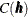 . Fix locations
. Fix locations 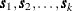 , and let
, and let 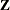 denote the random vector
denote the random vector
![\[ \mb{Z} = \left[ \begin{array}{c} Z(\bm {s}_1)\\ Z(\bm {s}_2)\\ \vdots \\ Z(\bm {s}_ k) \end{array} \right] \]](images/statug_sim2d0092.png)
with corresponding covariance matrix
![\[ \mb{C}_ z = \left( \begin{array}{cccc} C(\Strong{0}) & C(\bm {s}_1-\bm {s}_2) & \cdots & C(\bm {s}_1-\bm {s}_ k)\\ C(\bm {s}_2-\bm {s}_1) & C(\Strong{0}) & \cdots & C(\bm {s}_2-\bm {s}_ k)\\ & \ddots & & \\ C(\bm {s}_ k-\bm {s}_1) & C(\bm {s}_ k-\bm {s}_2) & \cdots & C(\Strong{0}) \end{array} \right) \]](images/statug_sim2d0093.png)
Since this covariance matrix is symmetric and positive definite, it has a Cholesky root, and the 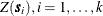 , can be simulated as described previously. This is how the SIM2D procedure implements unconditional simulation in the zero-mean
case. More generally,
, can be simulated as described previously. This is how the SIM2D procedure implements unconditional simulation in the zero-mean
case. More generally,
![\[ Z(\bm {s}) = \mu (\bm {s}) + \varepsilon (\bm {s}) \]](images/statug_sim2d0095.png)
where 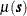 is a quadratic form in the coordinates
is a quadratic form in the coordinates 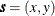 and the
and the 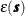 is an SRF that has the same covariance matrix
is an SRF that has the same covariance matrix 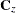 as previously. In this case, the
as previously. In this case, the 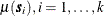 , is computed once and added to the simulated vector
, is computed once and added to the simulated vector 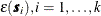 , for each realization.
, for each realization.
For a conditional simulation, this distribution of
![\[ \mb{Z} = \left[ \begin{array}{c} Z(\bm {s}_1)\\ Z(\bm {s}_2)\\ \vdots \\ Z(\bm {s}_ k) \end{array} \right] \]](images/statug_sim2d0092.png)
must be conditioned on the observed data. The relevant general result concerning
conditional distributions of multivariate normal random variables is the following. Let 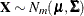 , where
, where
![\[ \mb{X} = \left[ \begin{array}{c} \mb{X}_1\\ \mb{X}_2\\ \end{array} \right] \]](images/statug_sim2d0101.png)
![\[ \bmu = \left[ \begin{array}{c} \bmu _1\\ \bmu _2\\ \end{array} \right] \]](images/statug_sim2d0102.png)
![\[ \bSigma = \left( \begin{array}{cc} \bSigma _{11} & \bSigma _{12}\\ \bSigma _{21} & \bSigma _{22}\\ \end{array} \right) \]](images/statug_sim2d0103.png)
The subvector 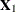 is
is 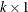 ,
, 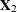 is
is 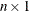 ,
, 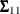 is
is 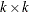 ,
, 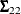 is
is 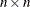 , and
, and 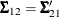 is
is 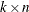 , with
, with 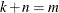 . The full vector
. The full vector 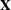 is partitioned into two subvectors,
is partitioned into two subvectors, 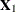 and
and 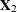 , and
, and 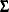 is similarly partitioned into covariances and cross covariances.
is similarly partitioned into covariances and cross covariances.
With this notation, the distribution of 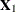 conditioned on
conditioned on 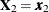 is
is 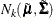 , with
, with
![\[ \tilde{\bmu }=\bmu _1+\bSigma _{12}\bSigma _{22}^{-1}(\bm {x}_2-\bmu _2) \]](images/statug_sim2d0118.png)
and
![\[ \tilde{\bSigma } = \bSigma _{11}-\bSigma _{12}\bSigma _{22}^{-1}\bSigma _{21} \]](images/statug_sim2d0119.png)
See Searle (1971, pp. 46–47) for details. The correspondence with the conditional spatial simulation problem is as follows. Let the coordinates
of the observed data points be denoted 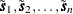 , with values
, with values 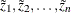 . Let
. Let 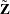 denote the random vector
denote the random vector
![\[ \tilde{\mb{Z}} = \left[ \begin{array}{c} Z(\tilde{\bm {s}}_1)\\ Z(\tilde{\bm {s}}_2)\\ \vdots \\ Z(\tilde{\bm {s}}_ n) \end{array} \right] \]](images/statug_sim2d0123.png)
The random vector 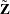 corresponds to
corresponds to 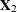 , while
, while 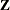 corresponds to
corresponds to 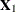 . Then
. Then 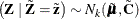 as in the previous distribution. The matrix
as in the previous distribution. The matrix
![\[ \tilde{\mb{C}} = \mb{C}_{11}-\mb{C}_{12}\mb{C}_{22}^{-1}\mb{C}_{21} \]](images/statug_sim2d0125.png)
is again positive definite, so a Cholesky factorization can be performed.
The dimension n for 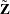 is simply the number of nonmissing observations for the VAR=
variable; the values
is simply the number of nonmissing observations for the VAR=
variable; the values 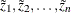 are the values of this variable. The coordinates
are the values of this variable. The coordinates 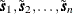 are also found in the DATA=
data set, with the variables that correspond to the x and y coordinates identified in the COORDINATES
statement.
Note: All VAR=
variables use the same set of conditioning coordinates; this fixes the matrix
are also found in the DATA=
data set, with the variables that correspond to the x and y coordinates identified in the COORDINATES
statement.
Note: All VAR=
variables use the same set of conditioning coordinates; this fixes the matrix 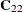 for all simulations.
for all simulations.
The dimension k for 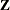 is the number of grid points specified in the GRID
statement. Since there is a single GRID
statement, this fixes the matrix
is the number of grid points specified in the GRID
statement. Since there is a single GRID
statement, this fixes the matrix 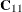 for all simulations. Similarly,
for all simulations. Similarly, 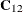 is fixed.
is fixed.
The Cholesky factorization 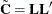 is computed once, as is the mean correction
is computed once, as is the mean correction
![\[ \tilde{\bmu }=\bmu _1+\mb{C}_{12}\mb{C}_{22}^{-1}(\bm {x}_2-\bmu _2) \]](images/statug_sim2d0131.png)
The means 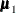 and
and 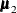 are computed using the grid coordinates
are computed using the grid coordinates  , the data coordinates
, the data coordinates 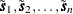 , and the quadratic form specification from the MEAN
statement. The simulation is now performed exactly as in the unconditional case. A
, and the quadratic form specification from the MEAN
statement. The simulation is now performed exactly as in the unconditional case. A 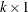 vector of independent standard
vector of independent standard 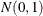 random variables is generated and multiplied by
random variables is generated and multiplied by  , and
, and 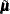 is added to the transformed vector. This is repeated N times, where N is the value specified for the NR= option.
is added to the transformed vector. This is repeated N times, where N is the value specified for the NR= option.
