The PLAN Procedure
Example 86.7 Crossover Designs
In crossover experiments, the same experimental units or subjects are given multiple treatments in sequence, and the model for the response at any one period includes an effect for the treatment applied in the previous period. A good design for a crossover experiment is therefore one that balances how often each treatment is preceded by each other treatment. Cox (1992) gives the following example of a balanced crossover experiment for paper production. In this experiment, the subjects are production runs of the mill, with the treatments being six different concentrations of pulp used in sequence. The following statements construct this design in a standard form:
proc plan; factors Run=6 ordered Period=6 ordered; treatments Treatment=6 cyclic (1 2 6 3 5 4); run;
Output 86.7.1 shows the results of the preceding statements.
Output 86.7.1: Crossover Design for Six Treatments
The construction method for this example is due to Williams (1949). The initial block for the treatment variable Treatment is defined as follows for n = 6:
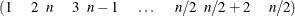
This general form serves to generate a balanced crossover design for n treatments and n subjects in n periods when n is even. When n is odd, 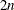 subjects are required, with the following initial blocks, respectively for odd and even n:
subjects are required, with the following initial blocks, respectively for odd and even n:
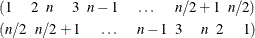
In order to randomize Williams’ crossover designs, the following statements randomly permute the subjects and treatments:
proc plan seed=136149876;
factors Run=6 ordered Period=6 ordered / noprint;
treatments Treatment=6 cyclic (1 2 6 3 5 4);
output out=RandomizedDesign
Run random
Treatment random
;
run;
/* / Relabel Period to obtain the same design as in Cox (1992). /------------------------------------------------------------------*/ data RandomizedDesign; set RandomizedDesign; Period = mod(Period+2,6)+1; run;
proc sort data=RandomizedDesign; by Run Period; run; proc transpose data=RandomizedDesign out=tDesign(drop=_name_); by notsorted Run; var Treatment; run; data tDesign; set tDesign; rename COL1-COL6 = Period_1-Period_6; run; proc print data=tDesign noobs; run;
In the preceding statements, Run and Treatment are randomized by using the RANDOM
option in the OUTPUT
statement, and new labels for Period are obtained in a subsequent DATA step. This Period relabeling is not necessary and might not be valid for Williams’ designs in general; it is used in this example only to match
results with those of Cox (1992). The SORT and TRANSPOSE steps then prepare the design to be printed in a standard form, shown in Output 86.7.2.
Output 86.7.2: Randomized Crossover Design
The analysis of a crossover experiment requires for each observation a carryover variable whose values are the treatment in the preceding period. The following statements add such a variable to the randomized design constructed previously:
proc sort data=RandomizedDesign; by Run Period; run; data RandomizedDesign; set RandomizedDesign; by Run period; LagTreatment = lag(Treatment); if (first.Run) then LagTreatment = .; run; proc transpose data=RandomizedDesign out=tDesign(drop=_name_); by notsorted Run; var LagTreatment; run; data tDesign; set tDesign; rename COL1-COL6 = Period_1-Period_6; run; proc print data=tDesign noobs; run;
Output 86.7.3 displays the values of the carryover variable for each run and period.
Output 86.7.3: Lag Treatment Effect in Crossover Design
Of course, the carryover variable has no effect in the first period, which is why it is coded with a missing value in this case.
The LAG effect in the EFFECT statement in PROC ORTHOREG provides a convenient mechanism for incorporating the carryover effect
into the analysis. The following statements first add the observed data to the design to create the Mills data set. Then PROC ORTHOREG is invoked, and the carryover effect is defined as a lag effect with the relevant period and
subject information specified. ODS is used to trim down the results to show only the parts that are usually of interest in
crossover analysis. For more information about the EFFECTS statement in PROC ORTHOREG, see the section EFFECT Statement in Chapter 84: The ORTHOREG Procedure.
data Responses; input Response @@; datalines; 56.7 53.8 54.4 54.4 58.9 54.5 58.5 60.2 61.3 54.4 59.1 59.8 55.7 60.7 56.7 59.9 56.6 59.6 57.3 57.7 55.2 58.1 60.2 60.2 53.7 57.1 59.2 58.9 58.9 59.6 58.1 55.7 58.9 56.6 59.6 57.5 ; data Mills; merge RandomizedDesign Responses; run;
proc orthoreg data=Mills; class Run Period Treatment; effect CarryOver = lag(Treatment / period=Period within=Run); model Response = Run Period Treatment CarryOver; test Run Period Treatment CarryOver / htype=1; lsmeans Treatment CarryOver / diff=anom; ods select Tests1 LSMeans Diffs; run;
Output 86.7.4 shows the carryover analysis that results from the preceding statements.
Output 86.7.4: Carryover Analysis for Crossover Experiment
| Differences of Treatment Least Squares Means | ||||||
|---|---|---|---|---|---|---|
| Treatment | _Treatment | Estimate | Standard Error | DF | t Value | Pr > |t| |
| 1 | Avg | -0.5185 | 0.2948 | 15 | -1.76 | 0.0990 |
| 2 | Avg | -0.09345 | 0.2948 | 15 | -0.32 | 0.7556 |
| 3 | Avg | 1.4780 | 0.2948 | 15 | 5.01 | 0.0002 |
| 4 | Avg | 1.5149 | 0.2948 | 15 | 5.14 | 0.0001 |
| 5 | Avg | 0.2690 | 0.2948 | 15 | 0.91 | 0.3758 |
| 6 | Avg | -2.6500 | 0.2948 | 15 | -8.99 | <.0001 |
| Differences of CarryOver Least Squares Means | ||||||
|---|---|---|---|---|---|---|
| CarryOver | _CarryOver | Estimate | Standard Error | DF | t Value | Pr > |t| |
| 1 | Avg | 0.3726 | 0.3284 | 15 | 1.13 | 0.2743 |
| 2 | Avg | -0.2774 | 0.3284 | 15 | -0.84 | 0.4116 |
| 3 | Avg | 0.6512 | 0.3284 | 15 | 1.98 | 0.0660 |
| 4 | Avg | -1.3274 | 0.3284 | 15 | -4.04 | 0.0011 |
| 5 | Avg | 1.3976 | 0.3284 | 15 | 4.26 | 0.0007 |
| 6 | Avg | -0.8167 | 0.3284 | 15 | -2.49 | 0.0252 |
The Type I analysis of variance indicates that all effects are significant—in particular, both the direct and the carryover effects of the treatment. In the presence of carryover effects, the LS-means need to be defined with some care. The LS-means for treatments computed using balanced margins for the carryover effect are inestimable; so the OBSMARGINS option is specified in the LSMEANS statement in order to use the observed margins instead. The observed margins take the absence of a carryover effect in the first period into account. Note that the LS-means themselves of the carryover effect are inestimable, but their differences are estimable. The LS-means of the direct effect of the treatment and the ANOM differences for the LS-means of their carryover effect match the "adjusted direct effects" and "adjusted residual effects," respectively, of Cox (1992).
