The ORTHOREG Procedure

The ORTHOREG procedure fits general linear models by the method of least squares. Other SAS/STAT software procedures, such as the GLM and REG procedures, fit the same types of models, but PROC ORTHOREG can produce more accurate estimates than other regression procedures when your data are ill-conditioned. Instead of collecting crossproducts, PROC ORTHOREG uses Gentleman-Givens transformations to update and compute the upper triangular matrix 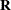of the QR decomposition of the data matrix, with special care for scaling (Gentleman 1972, 1973). This method has the advantage over other orthogonalization methods (for example, Householder transformations) of not requiring the data matrix to be stored in memory.

The standard SAS regression procedures (PROC REG and PROC GLM) are very accurate for most problems. However, if you have very ill-conditioned data, these procedures can produce estimates that yield an error sum of squares very close to the minimum but still different from the exact least squares estimates. Normally, this coincides with estimates that have very high standard errors. In other words, the numerical error is much smaller than the statistical standard error.

PROC ORTHOREG fits models by the method of linear least squares, minimizing the sum of the squared residuals for predicting the responses—that is, the distance between the regression line and the observed Ys. The "ORTHO" in the name of the procedure refers to the orthogonalization approach to solving the least squares equations. In particular, PROC ORTHOREG does not perform the modeling method known as "orthogonal regression," which minimizes a different criterion (namely, the distance between the regression line and the X/Y points taken together.)