The NESTED Procedure

A random-effects model for data from a completely nested design with n factors has the general form

$y_{i_1 i_2 \cdots i_ n r} = \mu + \alpha _{i_1} + \beta _{i_1 i_2} + \cdots + \epsilon _{i_1 i_2 \cdots i_ n r}$

where

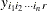
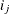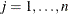$y_{i_1 i_2 \cdots i_ n r}$: is the value of the dependent variable observed at the rth replication with factor j at level $i_ j$ , for $j=1,\ldots ,n$ .
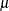
$\mu$: is the overall (fixed) mean of the sampled population.
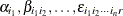
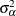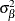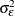$\alpha _{i_1},\beta _{i_1 i_2},\ldots , \epsilon _{i_1 i_2 \cdots i_ n r}$: are mutually uncorrelated random effects with zero means and respective variances $\sigma _{\alpha }^2$ , $\sigma _{\beta }^2$ , …, $\sigma _{\epsilon }^2$ .