The MULTTEST Procedure

Agresti, A. (2002). Categorical Data Analysis. 2nd ed. New York: John Wiley & Sons.

Allison, D. B., Gadbury, G. L., Moonseong, H., Fernández, J. R., Lee, C., Prolla, T. A., and Weindruch, R. (2002). “A Mixture Model Approach for the Analysis of Microarray Gene Expression Data.” Computational Statistics and Data Analysis 39:1–20.

Armitage, P. (1955). “Tests for Linear Trend in Proportions and Frequencies.” Biometrics 11:375–386.

Benjamini, Y., and Hochberg, Y. (1995). “Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing.” Journal of the Royal Statistical Society, Series B 57:289–300.

Benjamini, Y., and Hochberg, Y. (2000). “On the Adaptive Control of the False Discovery Rate in Multiple Testing with Independent Statistics.” Journal of Educational and Behavioral Statistics 25:60–83.

Benjamini, Y., Krieger, A. M., and Yekutieli, D. (2006). “Adaptive Linear Step-Up False Discovery Rate Controlling Procedures.” Biometrika 93:491–507.

Benjamini, Y., and Yekutieli, D. (2001). “The Control of the False Discovery Rate in Multiple Testing under Dependency.” Annals of Statistics 29:1165–1188.

Bickis, M., and Krewski, D. (1986). “Statistical Issues in the Analysis of the Long Term Carcinogenicity Bioassay in Small Rodents: An Empirical Evaluation of Statistical Decision Rules.” Environmental Health Directorate, Health Protection Branch, Health and Welfare Canada, Ottawa, Ontario.

Brown, B. W., and Russell, K. (1997). “Methods Correcting for Multiple Testing: Operating Characteristics.” Statistics in Medicine 16:2511–2528.

Brown, C. C., and Fears, T. R. (1981). “Exact Significance Levels for Multiple Binomial Testing with Application to Carcinogenicity Screens.” Biometrics 37:763–774.

Cochran, W. G. (1954). “Some Methods for Strengthening the Common 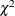Tests.” Biometrics 10:417–451.

Dinse, G. E. (1985). “Testing for Trend in Tumor Prevalence Rates, Part 1: Nonlethal Tumors.” Biometrics 41:751–770.

Dmitrienko, A., Molenberghs, G., Chuang-Stein, C., and Offen, W. (2005). Analysis of Clinical Trials Using SAS: A Practical Guide. Cary, NC: SAS Institute Inc.

Dudoit, S., Shaffer, J. P., and Boldrick, J. C. (2003). “Multiple Hypothesis Testing in Microarray Experiments.” Statistical Science 18:71–103.

Freedman, D. A. (1981). “Bootstrapping Regression Models.” Annals of Statistics 9:1218–1228.

Freeman, M. F., and Tukey, J. W. (1950). “Transformations Related to the Angular and the Square Root.” Annals of Mathematical Statistics 21:607–611.

Gibson, G., and Wolfinger, R. D. (2004). “Gene Expression Profiling Using Mixed Models.” In Genetic Analysis of Complex Traits Using SAS, edited by A. M. Saxton, 251–278. Cary, NC: SAS Institute Inc.

Good, I. J. (1987). “A Survey of the Use of the Fast Fourier Transform for Computing Distributions.” Journal of Statistical Computation and Simulation 28:87–93.

Heyse, J., and Rom, D. (1988). “Adjusting for Multiplicity of Statistical Tests in the Analysis of Carcinogenicity Studies.” Biometrical Journal 30:883–896.

Hochberg, Y. (1988). “A Sharper Bonferroni Procedure for Multiple Significance Testing.” Biometrika 75:800–803.

Hochberg, Y., and Benjamini, Y. (1990). “More Powerful Procedures for Multiple Significance Testing.” Statistics in Medicine 9:811–818.

Hochberg, Y., and Tamhane, A. C. (1987). Multiple Comparison Procedures. New York: John Wiley & Sons.

Hoel, D. G., and Walburg, H. E. (1972). “Statistical Analysis of Survival Experiments.” Journal of the National Cancer Institute 49:361–372.

Holland, B. S., and Copenhaver, M. D. (1987). “An Improved Sequentially Rejective Bonferroni Test Procedure.” Biometrics 43:417–424.

Holm, S. (1979). “A Simple Sequentially Rejective Multiple Test Procedure.” Scandinavian Journal of Statistics 6:65–70.

Hommel, G. (1988). “A Comparison of Two Modified Bonferroni Procedures.” Biometrika 75:383–386.

Hsueh, H., Chen, J. J., and Kodell, R. L. (2003). “Comparison of Methods for Estimating the Number of True Null Hypotheses in Multiplicity Testing.” Journal of Biopharmaceutical Statistics 13:675–689.

Lagakos, S. W., and Louis, T. A. (1985). “The Statistical Analysis of Rodent Tumorigenicity Experiments.” In Toxicological Risk Assessment, edited by D. B. Clayson, D. Krewski, and I. Munro, 144–163. Boca Raton, FL: CRC Press.

Liu, W. (1996). “Multiple Tests of a Non-hierarchical Finite Family of Hypotheses.” Journal of the Royal Statistical Society, Series B 58:455–461.

Mantel, N. (1980). “Assessing Laboratory Evidence for Neoplastic Activity.” Biometrics 36:381–399.

Mantel, N., and Haenszel, W. (1959). “Statistical Aspects of Analysis of Data from Retrospective Studies of Disease.” Journal of the National Cancer Institute 22:719–748.

Marcus, R., Peritz, E., and Gabriel, K. R. (1976). “On Closed Testing Procedures with Special Reference to Ordered Analysis of Variance.” Biometrika 63:655–660.

Miller, J. J. (1978). “The Inverse of the Freeman-Tukey Double Arcsine Transformation.” American Statistician 32:138.

Osborne, J. A. (2006). “Estimating the False Discovery Rate Using SAS.” In Proceedings of the Thirty-First Annual SAS Users Group International Conference. Cary, NC: SAS Institute Inc. http://www2.sas.com/proceedings/sugi31/190-31.pdf.

Pagano, M., and Tritchler, D. (1983). “On Obtaining Permutation Distributions in Polynomial Time.” Journal of the American Statistical Association 78:435–440.

Peto, R., Pike, M. C., Day, N. E., Gray, R. G., Lee, P. N., Parish, S., Peto, J., Richards, S., and Wahrendorf, J. (1980). “Guidelines for Simple, Sensitive Significance Tests for Carcinogenic Effects in Long-Term Animal Experiments.” In Suppl. 2: Long-Term and Short-Term Screening Assays for Carcinogens—a Critical Appraisal, 311–426. IARC Monographs on the Evaluation of Carcinogenic Risks to Humans. Lyon: International Agency for Research on Cancer.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1992). Numerical Recipes in C: The Art of Scientific Computing. 2nd ed. Cambridge: Cambridge University Press.

Sarkar, S. K., and Chang, C.-K. (1997). “The Simes Method for Multiple Hypothesis Testing with Positively Dependent Test Statistics.” Journal of the American Statistical Association 92:1601–1608.

Satterthwaite, F. E. (1946). “An Approximate Distribution of Estimates of Variance Components.” Biometrics Bulletin 2:110–114.

Schweder, T., and Spjøtvoll, E. (1982). “Plots of P-Values to Evaluate Many Tests Simultaneously.” Biometrika 69:493–502.

Shaffer, J. P. (1986). “Modified Sequentially Rejective Multiple Test Procedures.” Journal of the American Statistical Association 81:826–831.

Šidák, Z. (1967). “Rectangular Confidence Regions for the Means of Multivariate Normal Distributions.” Journal of the American Statistical Association 62:626–633.

Simes, R. J. (1986). “An Improved Bonferroni Procedure for Multiple Tests of Significance.” Biometrika 73:751–754.

Soper, K. A., and Tonkonoh, N. (1993). “The Discrete Distribution Used for the Log-Rank Test Can Be Inaccurate.” Biometrical Journal 35:291–298.

Storey, J. D. (2002). “A Direct Approach to False Discovery Rates.” Journal of the Royal Statistical Society, Series B 64:479–498.

Storey, J. D., Taylor, J. E., and Siegmund, D. (2004). “Strong Control, Conservative Point Estimation, and Simultaneous Conservative Consistency of False Discovery Rates: A Unified Approach.” Journal of the Royal Statistical Society, Series B 66:187–205.

Storey, J. D., and Tibshirani, R. (2003). “Statistical Significance for Genomewide Studies.” Proceedings of the National Academy of Sciences USA 100:9440–9445.

Turkheimer, F. E., Smith, C. B., and Schmidt, K. (2001). “Estimation of the Number of 'True' Null Hypotheses in Multivariate Analysis of Neuroimaging Data.” NeuroImage 13:920–930.

Westfall, P. H. (2005). “Combining P Values.” In Encyclopedia of Biostatistics, 2nd ed., edited by P. Armitage, and T. Colton. Chichester, UK: John Wiley & Sons.

Westfall, P. H., and Lin, Y. (1988). “Estimating Optimal Continuity Corrections in Run Time.” In Proceedings of the Statistical Computing Section, 297–298. Alexandria, VA: American Statistical Association.

Westfall, P. H., and Soper, K. A. (1994). “Nonstandard Uses of PROC MULTTEST: Permutational Peto Tests; Permutational and Unconditional t and Binomial Tests.” In Proceedings of the Nineteenth Annual SAS Users Group International Conference, 986–989. Cary, NC: SAS Institute Inc. http://www.sascommunity.org/sugi/SUGI94/Sugi-94-173%20Westfall%20Soper.pdf.

Westfall, P. H., Tobias, R. D., Rom, D., Wolfinger, R. D., and Hochberg, Y. (1999). Multiple Comparisons and Multiple Tests Using the SAS System. Cary, NC: SAS Institute Inc.

Westfall, P. H., and Wolfinger, R. D. (1997). “Multiple Tests with Discrete Distributions.” American Statistician 51:3–8.

Westfall, P. H., and Wolfinger, R. D. (2000). “Closed Multiple Testing Procedures and PROC MULTTEST.” Observations (June).

Westfall, P. H., and Young, S. S. (1989). “P-Value Adjustments for Multiple Tests in Multivariate Binomial Models.” Journal of the American Statistical Association 84:780–786.

Westfall, P. H., and Young, S. S. (1993). Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment. New York: John Wiley & Sons.

Yates, F. (1984). “Tests of Significance for 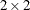Contingency Tables.” Journal of the Royal Statistical Society, Series A 147:426–463.

Yekutieli, D., and Benjamini, Y. (1999). “Resampling-Based False Discovery Rate Controlling Multiple Test Procedures for Correlated Test Statistics.” Journal of Statistical Planning and Inference 82:171–196.