The MODECLUS Procedure

Clustering Methods

Subsections:

The number of clusters is a function of the smoothing parameters. The number of clusters tends to decrease as the smoothing parameters increase, but the relationship is not strictly monotonic. Generally, you should specify several different values of the smoothing parameters to see how the number of clusters varies.

The clustering methods used by PROC MODECLUS use spherical clustering neighborhoods of fixed or variable radius that are similar to the spherical kernels used for density estimation. For fixed-radius neighborhoods, specify the radius as a Euclidean distance with either the CR= or R= option. For variable-radius neighborhoods, specify the number of neighbors desired within the sphere with either the CK= or K= option; the radius is then the smallest radius that contains at least the specified number of observations including the observation for which the neighborhood is being determined. However, in the following descriptions of clustering methods, an observation is not considered to be one of its own neighbors. If you specify both the CR= or R= option and the CK= or K= option, the radius used is the maximum of the two indicated radii; this is useful for dealing with outliers. In this section, the symbols 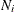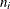$N_ i$, $N_ i^{-}$, $n_ i$, and $n_ i^{-}$ refer to clustering neighborhoods, not density estimation neighborhoods.

METHOD=0

Begin with each observation in a separate cluster. For each observation and each of its neighbors, join the cluster to which the observation belongs with the cluster to which the neighbor belongs. This method does not use density estimates. With a fixed clustering radius, the clusters are those obtained by cutting the single linkage tree at the specified radius (see Chapter 33: The CLUSTER Procedure).

METHOD=1

Begin with each observation in a separate cluster. For each observation, find the nearest neighbor with a greater estimated density. If such a neighbor exists, join the cluster to which the observation belongs with the cluster to which the specified neighbor belongs.

Next, consider each observation with density estimates equal to that of one or more neighbors but not less than the estimate at any neighbor. Join the cluster containing the observation with (1) each cluster containing a neighbor of the observation such that the maximum density estimate in the cluster equals the density estimate at the observation and (2) the cluster containing the nearest neighbor of the observation such that the maximum density estimate in the cluster exceeds the density estimate at the observation.

This method is similar to the classification or assignment stage of algorithms described by Gitman (1973) and Huizinga (1978).

METHOD=2

Begin with each observation in a separate cluster. For each observation, find the neighbor with the greatest estimated density exceeding the estimated density of the observation. If such a neighbor exists, join the cluster to which the observation belongs with the cluster to which the specified neighbor belongs.

Observations with density estimates equal to that of one or more neighbors but not less than the estimate at any neighbor are treated the same way as they are in METHOD=1.

This method is similar to the first stage of an algorithm proposed by Mizoguchi and Shimura (1980).

METHOD=3

Begin with each observation in a separate cluster. For each observation, find the neighbor with greater estimated density such that the slope of the line connecting the point on the estimated density surface at the observation with the point on the estimated density surface at the neighbor is a maximum. That is, for observation 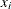$x_ i$, find a neighbor $x_ j$ such that ${(\hat{f}_ j - \hat{f}_ i)} / {\mbox{d}(x_ j,x_ i)}$ is a maximum. 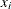If this slope is positive, join the cluster to which observation $x_ i$ belongs with the cluster to which the specified neighbor $x_ j$ belongs. This method was invented by Koontz, Narendra, and Fukunaga (1976).

Observations with density estimates equal to that of one or more neighbors but not less than the estimate at any neighbor are treated the same way as they are in METHOD=1. The algorithm suggested for this situation by Koontz, Narendra, and Fukunaga (1976) might fail for flat areas in the estimated density that contain four or more observations.

METHOD=4

This method is equivalent to the first stage of two-stage density linkage (see Chapter 33: The CLUSTER Procedure) without the use of the MODE=option.

METHOD=5

This method is equivalent to the first stage of two-stage density linkage (see Chapter 33: The CLUSTER Procedure) with the use of the MODE=option.

METHOD=6

Begin with all observations unassigned.

Step 1: Form a list of seeds, each seed being a single observation such that the estimated density of the observation is not less than the estimated density of any of its neighbors. If you specify the MAXCLUSTERS=n option, retain only the n seeds with the greatest estimated densities.

Step 2: Consider each seed in decreasing order of estimated density, as follows:

  1. If the current seed has already been assigned, proceed to the next seed. Otherwise, form a new cluster consisting of the current seed.

  2. Add to the cluster any unassigned seed that is a neighbor of a member of the cluster or that shares a neighbor with a member of the cluster; repeat until no unassigned seed satisfies these conditions.

  3. Add to the cluster all neighbors of seeds that belong to the cluster.

  4. Consider each unassigned observation. Compute the ratio of the sum of the p – 1 powers of the estimated density of the neighbors that belong to the current cluster to the sum of the p – 1 powers of the estimated density of all of its neighbors, where p is specified by the POWER= option and is 2 by default. Let 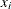$x_ i$ be the current observation, and let k be the index of the current cluster. Then this ratio is

    \[ r_{ik} = \frac{ \sum _{j\in {N_ i\cap {C_ k}}}\hat{f}_ j^{p-1} }{ \sum _{j\in {N_ i}}\hat{f}_ j^{p-1} } \]

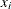(The sum of the p – 1 powers of the estimated density of the neighbors of an observation is an estimate of the integral of the pth power of the density over the neighborhood.) If $r_{ik}$ exceeds the maximum of 0.5 and the value of the THRESHOLD= option, add the observation $x_ i$ to the current cluster k. Repeat until no more observations can be added to the current cluster.

Step 3: (This step is performed only if the value of the THRESHOLD= option is less than 0.5.) Form a list of unassigned observations in decreasing order of estimated density. Repeat the following actions until the list is empty:

  1. Remove the first observation from the list, such as observation $x_ i$.

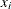  2. For each cluster k, compute $r_{ik}$.

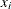  3. If the maximum over clusters of $r_{ik}$ exceeds the value of the THRESHOLD= option, assign observation $x_ i$ to the corresponding cluster and insert all observations of which the current observation is a neighbor into the list, keeping the list in decreasing order of estimated density.

METHOD=6 is related to a method invented by Koontz and Fukunaga (1972a) and discussed by Koontz and Fukunaga (1972b).