Introduction to Statistical Modeling with SAS/STAT Software
Bayesian Models
Statistical models based on the classical (or frequentist) paradigm treat the parameters of the model as fixed, unknown constants. They are not random variables, and the notion of probability is derived in an objective sense as a limiting relative frequency. The Bayesian paradigm takes a different approach. Model parameters are random variables, and the probability of an event is defined in a subjective sense as the degree to which you believe that the event is true. This fundamental difference in philosophy leads to profound differences in the statistical content of estimation and inference. In the frequentist framework, you use the data to best estimate the unknown value of a parameter; you are trying to pinpoint a value in the parameter space as well as possible. In the Bayesian framework, you use the data to update your beliefs about the behavior of the parameter to assess its distributional properties as well as possible.
Suppose you are interested in estimating 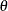 from data
from data ![$\bY = [Y_1, \ldots , Y_ n]$](images/statug_intromod0082.png) by using a statistical model described by a density
by using a statistical model described by a density 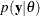 . Bayesian philosophy states that
. Bayesian philosophy states that 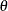 cannot be determined exactly, and uncertainty about the parameter is expressed through probability statements and distributions.
You can say, for example, that
cannot be determined exactly, and uncertainty about the parameter is expressed through probability statements and distributions.
You can say, for example, that 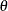 follows a normal distribution with mean 0 and variance 1, if you believe that this distribution best describes the uncertainty
associated with the parameter.
follows a normal distribution with mean 0 and variance 1, if you believe that this distribution best describes the uncertainty
associated with the parameter.
The following steps describe the essential elements of Bayesian inference:
-
A probability distribution for
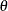 is formulated as
is formulated as 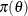 , which is known as the prior distribution, or just the prior. The prior distribution expresses your beliefs, for example, on the mean, the spread, the
skewness, and so forth, about the parameter prior to examining the data.
, which is known as the prior distribution, or just the prior. The prior distribution expresses your beliefs, for example, on the mean, the spread, the
skewness, and so forth, about the parameter prior to examining the data.
-
Given the observed data
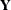 , you choose a statistical model
, you choose a statistical model 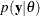 to describe the distribution of
to describe the distribution of 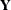 given
given 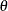 .
.
-
You update your beliefs about
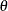 by combining information from the prior distribution and the data through the calculation of the posterior distribution,
by combining information from the prior distribution and the data through the calculation of the posterior distribution, 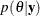 .
.
The third step is carried out by using Bayes’ theorem, from which this branch of statistical philosophy derives its name. The theorem enables you to combine the prior distribution and the model in the following way:
![\[ p(\theta | \mb{y}) = \frac{p(\theta , \mb{y})}{p(\mb{y})} = \frac{p(\mb{y} | \theta )\pi (\theta )}{p(\mb{y})}= \frac{p(\mb{y} | \theta )\pi (\theta )}{\int p(\mb{y} | \theta ) \pi (\theta )\, d\theta } \]](images/statug_intromod0086.png)
The quantity 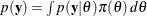 is the normalizing constant of the posterior distribution. It is also the marginal distribution of
is the normalizing constant of the posterior distribution. It is also the marginal distribution of 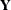 , and it is sometimes called the marginal distribution of the data.
, and it is sometimes called the marginal distribution of the data.
The likelihood function of 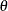 is any function proportional to
is any function proportional to 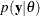 —that is,
—that is, 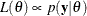 . Another way of writing Bayes’ theorem is
. Another way of writing Bayes’ theorem is
![\[ p(\theta | \mb{y}) = \frac{L(\theta ) \pi (\theta )}{\int L(\theta ) \pi (\theta ) \, d \theta } \]](images/statug_intromod0089.png)
The marginal distribution 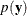 is an integral; therefore, provided that it is finite, the particular value of the integral does not yield any additional
information about the posterior distribution. Hence,
is an integral; therefore, provided that it is finite, the particular value of the integral does not yield any additional
information about the posterior distribution. Hence, 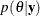 can be written up to an arbitrary constant, presented here in proportional form, as
can be written up to an arbitrary constant, presented here in proportional form, as
![\[ p(\theta | \mb{y}) \propto L(\theta ) \pi (\theta ) \]](images/statug_intromod0092.png)
Bayes’ theorem instructs you how to update existing knowledge with new information. You start from a prior belief 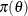 , and, after learning information from data
, and, after learning information from data 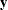 , you change or update the belief on
, you change or update the belief on 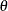 and obtain
and obtain 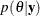 . These are the essential elements of the Bayesian approach to data analysis.
. These are the essential elements of the Bayesian approach to data analysis.
In theory, Bayesian methods offer a very simple alternative to statistical inference—all inferences follow from the posterior
distribution 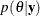 . However, in practice, only the most elementary problems enable you to obtain the posterior distribution analytically. Most
Bayesian analyses require sophisticated computations, including the use of simulation methods. You generate samples from the
posterior distribution and use these samples to estimate the quantities of interest.
. However, in practice, only the most elementary problems enable you to obtain the posterior distribution analytically. Most
Bayesian analyses require sophisticated computations, including the use of simulation methods. You generate samples from the
posterior distribution and use these samples to estimate the quantities of interest.
Both Bayesian and classical analysis methods have their advantages and disadvantages. Your choice of method might depend on the goals of your data analysis. If prior information is available, such as in the form of expert opinion or historical knowledge, and you want to incorporate this information into the analysis, then you might consider Bayesian methods. In addition, if you want to communicate your findings in terms of probability notions that can be more easily understood by nonstatisticians, Bayesian methods might be appropriate. The Bayesian paradigm can provide a framework for answering specific scientific questions that a single point estimate cannot sufficiently address. On the other hand, if you are interested in estimating parameters and in formulating inferences based on the properties of the parameter estimators, then there is no need to use Bayesian analysis. When the sample size is large, Bayesian inference often provides results for parametric models that are very similar to the results produced by classical, frequentist methods.
For more information, see Chapter 7: Introduction to Bayesian Analysis Procedures.