Introduction to Statistical Modeling with SAS/STAT Software
Latent Variable Models
Latent variable modeling involves variables that are not observed directly in your research. It has a relatively long history, dating back from the measure of general intelligence by common factor analysis (Spearman 1904) to the emergence of modern-day structural equation modeling (Jöreskog 1973; Keesling 1972; Wiley 1973).
Latent variables are involved in almost all kinds of regression models. In a broad sense, all additive error terms in regression
models are latent variables simply because they are not measured in research. Hereafter, however, a narrower sense of latent
variables is used when referring to latent variable models. Latent variables are systematic unmeasured variables that are also referred to as factors. For example, in the following diagram a simple relation between Emotional Intelligence and Career Achievement is shown:
Figure 3.1:
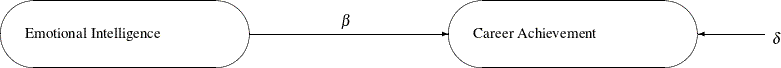
In the diagram, both Emotional Intelligence and Career Achievement are treated as latent factors. They are hypothetical constructs in your model. You hypothesize that Emotional Intelligence is a "causal factor" or predictor of Career Achievement. The symbol 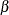 represents the regression coefficient or the effect of
represents the regression coefficient or the effect of Emotional Intelligence on Career Achievement. However, the "causal relationship" or prediction is not perfect. There is an error term 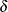 , which accounts for the unsystematic part of the prediction. You can represent the preceding diagram by using the following
linear equation:
, which accounts for the unsystematic part of the prediction. You can represent the preceding diagram by using the following
linear equation:
![\[ \mbox{CA} = \beta \mbox{EI} + \delta \]](images/statug_intromod0060.png)
where CA represents Career Achievement and EI represents Emotional Intelligence. The means of the latent factors in the linear model are arbitrary, and so they are assumed to be zero. The error variable
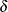 also has a zero mean with an unknown variance. This equation represents the so-called "structural model," where the "true"
relationships among latent factors are theorized.
also has a zero mean with an unknown variance. This equation represents the so-called "structural model," where the "true"
relationships among latent factors are theorized.
In order to model this theoretical model with latent factors, some observed variables must somehow relate to these factors.
This calls for the measurement models for latent factors. For example, Emotional Intelligence could be measured by some established tests. In these tests, individuals are asked to respond to certain special situations
that involve stressful decision making, personal confrontations, and so on. Their responses to these situations are then rated
by experts or a standardized scoring system. Suppose there are three such tests and the test scores are labeled as X1, X2 and X3, respectively. The measurement model for the latent factor Emotional Intelligence is specified as follows:
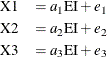
where 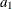 ,
,  , and
, and 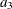 are regression coefficients and
are regression coefficients and 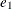 ,
, 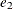 , and
, and 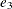 are measurement errors. Measurement errors are assumed to be independent of the latent factors EI and CA. In the measurement
model,
are measurement errors. Measurement errors are assumed to be independent of the latent factors EI and CA. In the measurement
model, X1, X2, and X3 are called the indicators of the latent variable EI. These observed variables are assumed to be centered in the model, and
therefore no intercept terms are needed. Each of the indicators is a scaled measurement of the latent factor EI plus a unique
error term.
Similarly, you need to have a measurement model for the latent factor CA. Suppose that there are four observed indicators
Y1, Y2, Y3, and Y4 (for example, Job Status) for this latent factor. The measurement model for CA is specified as follows:
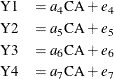
where 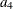 ,
, 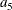 ,
, 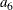 , and
, and 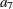 are regression coefficients and
are regression coefficients and 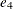 ,
, 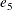 ,
, 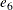 , and
, and 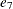 are error terms. Again, the error terms are assumed to be independent of the latent variables EI and CA, and
are error terms. Again, the error terms are assumed to be independent of the latent variables EI and CA, and Y1, Y2, Y3, and Y4 are centered in the equations.
Given the data for the measured variables, you analyze the structural and measurement models simultaneously by the structural
equation modeling techniques. In other words, estimation of 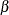 ,
, 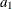 –
–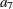 , and other parameters in the model are carried out simultaneously in the modeling.
, and other parameters in the model are carried out simultaneously in the modeling.
Modeling involving the use of latent factors is quite common in social and behavioral sciences, personality assessment, and marketing research. Hypothetical constructs, although not observable, are very important in building theories in these areas.
Another use of latent factors in modeling is to "purify" the predictors in regression analysis. A common assumption in linear regression models is that predictors are measured without errors. That is, in the following linear equation x is assumed to have been measured without errors:
![\[ y = \alpha + \beta x + \epsilon \]](images/statug_intromod0077.png)
However, if x has been contaminated with measurement errors that cannot be ignored, the estimate of 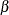 might be biased severely so that the true relationship between x and y would be masked.
might be biased severely so that the true relationship between x and y would be masked.
A measurement model for x provides a solution to such a problem. Let 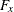 be a "purified" version of x. That is,
be a "purified" version of x. That is, 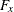 is the "true" measure of x without measurement errors, as described in the following equation:
is the "true" measure of x without measurement errors, as described in the following equation:
![\[ x = F_ x + \delta \]](images/statug_intromod0079.png)
where 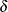 represents a random measurement error term. Now, the linear relationship of interest is specified in the following new linear
regression equation:
represents a random measurement error term. Now, the linear relationship of interest is specified in the following new linear
regression equation:
![\[ y = \alpha + \beta F_ x + \epsilon \]](images/statug_intromod0080.png)
In this equation, 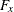 , which is now free from measurement errors, replaces x in the original equation. With measurement errors taken into account in the simultaneous fitting of the measurement and the
new regression equations, estimation of
, which is now free from measurement errors, replaces x in the original equation. With measurement errors taken into account in the simultaneous fitting of the measurement and the
new regression equations, estimation of 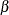 is unbiased; hence it reflects the true relationship much better.
is unbiased; hence it reflects the true relationship much better.
Certainly, introducing latent factors in models is not a "free lunch." You must pay attention to the identification issues induced by the latent variable methodology. That is, in order to estimate the parameters in structural equation models with latent variables, you must set some identification constraints in these models. There are some established rules or conventions that would lead to proper model identification and estimation. See Chapter 17: Introduction to Structural Equation Modeling with Latent Variables, for examples and general details.
In addition, because of the nature of latent variables, estimation in structural equation modeling with latent variables does not follow the same form as that of linear regression analysis. Instead of defining the estimators in terms of the data matrices, most estimation methods in structural equation modeling use the fitting of the first- and second- order moments. Hence, estimation principles described in the section Classical Estimation Principles do not apply to structural equation modeling. However, you can see the section Estimation Criteria in Chapter 29: The CALIS Procedure, for details about estimation in structural equation modeling with latent variables.