Introduction to Mixed Modeling Procedures

Linear Mixed Models

Subsections:

You can fit linear mixed models in SAS/STAT software with the GLM, GLIMMIX, HPMIXED, LATTICE, MIXED, NESTED, and VARCOMP procedures.

The procedure specifically designed for statistical estimation in linear mixed models is the MIXED procedure. To fit the linear mixed model

\begin{align*} \bY =& \, \, \bX \bbeta + \bZ \bgamma + \bepsilon \\ \bgamma \sim & \, \, N(\mb{0},\bG ) \\ \bepsilon \sim & \, \, N(\mb{0},\bR ) \\ \mr{Cov}[\bgamma ,\bepsilon ] =& \, \, \mb{0} \end{align*}

with the MIXED procedure, you specify the fixed-effects design matrix 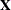$\bX $ in the MODEL statement, the random-effects design matrix 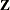$\bZ $ in the RANDOM statement, the covariance matrix of the random effects 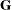$\bG $ with options (SUBJECT=, GROUP=, TYPE=) in the RANDOM statement, and the 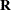$\bR $ matrix in the REPEATED statement.

By default, covariance parameters are estimated by restricted (residual) maximum likelihood. In supported models, the METHOD=TYPE1, METHOD=TYPE2, and METHOD=TYPE3 options lead to method-of-moment-based estimators and analysis of variance. The MIXED procedure provides an extensive list of diagnostics for mixed models, from various residual graphics to observationwise and groupwise influence diagnostics.

The NESTED procedure performs an analysis of variance in nested random effects models. The VARCOMP procedure can be used to estimate variance components associated with random effects in random and mixed models. The LATTICE procedure computes analysis of variance for balanced and partially balanced square lattices. You can fit the random and mixed models supported by these procedures with the MIXED procedure as well. Some specific analyses, such as the analysis of Gauge R & R studies in the VARCOMP procedure (Burdick, Borror, and Montgomery 2005), are unique to the specialized procedures.

The GLIMMIX procedure can fit most of the models that you can fit with the MIXED procedure, but it does not offer method-of-moment-based estimation and analysis of variance in the narrow sense. Also, PROC GLIMMIX does not support the same array of covariance structures as the MIXED procedure and does not support a sampling-based Bayesian analysis. An in-depth comparison of the GLIMMIX and MIXED procedures can be found in the section Comparing the GLIMMIX and MIXED Procedures, in Chapter 45: The GLIMMIX Procedure.