Shared Concepts and Topics

Natural cubic splines are cubic splines with the additional restriction that the splines are required to be linear beyond the extreme knots. Some authors prefer the terminology "restricted cubic splines" to "natural cubic splines." The space of unrestricted cubic splines on n knots has the dimension 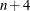. Imposing the restrictions that the cubic polynomials beyond the first and last knot reduce to linear polynomials reduces the number of degrees of freedom by 4, and so a basis for the natural cubic splines consists of n functions. Starting from the truncated power function basis for the unrestricted cubic splines, you can obtain a reduced basis by imposing linearity constraints. 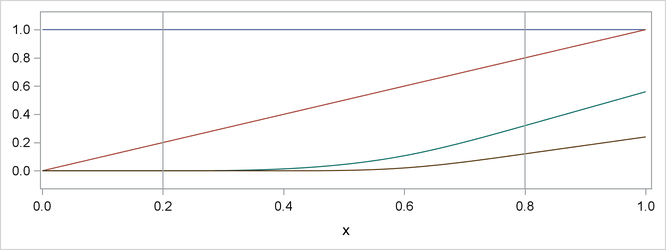You can find details about this construction in Hastie, Tibshirani, and Friedman (2001). Figure 19.5 shows this natural cubic spline basis defined on with four equally spaced internal knots at 0.2, 0.4, 0.6, and 0.8. Note that this basis consists of four basis functions that are all linear beyond the extreme knots at 0.2 and 0.8.