The HPPRINCOMP Procedure
NIPALS
The nonlinear iterative partial least squares (NIPALS) method extracts the principal components successively based on the
data matrix 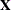 . The NIPALS method starts by calculating the loadings,
. The NIPALS method starts by calculating the loadings, 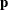 , as
, as 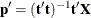 , where
, where 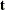 is the score vector. It then calculates an improved score vector,
is the score vector. It then calculates an improved score vector, 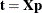 . The method iteratively computes the improved
. The method iteratively computes the improved 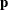 and
and 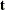 until convergence is reached.
until convergence is reached.
This process accounts for how the first principal component is extracted. The second component is extracted in the same way,
by replacing 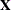 with the residual from the first component:
with the residual from the first component: 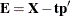 .
.
For large data matrices or matrices that have a high degree of column collinearity, the NIPALS method suffers from loss of orthogonality because of the machine-precision errors that accumulate at each iteration step. In practice, the NIPALS method is used to extract only the first few principal components.
