The HPPRINCOMP Procedure

Eigenvalue Decomposition

Let 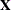$\mb{X}$ be a centered and scaled data matrix that has k numerical variables. The eigenvalue decomposition method bases the component extraction on the eigenvalue decomposition of the covariance matrix 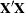$\mb{X}’\mb{X}$, which extracts all the k principal components simultaneously. Each principal component is a linear combination of the original variables, and each component is orthogonal, with coefficients equal to the eigenvectors of the covariance matrix 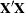$\mb{X}’\mb{X}$. The eigenvectors are usually normalized to have unit length. The principal components are sorted by descending order of the eigenvalues, which are equal to the variances of the components.