The HPFMM Procedure
Log-Likelihood Functions for Response Distributions
The HPFMM procedure calculates the log likelihood that corresponds to a particular response distribution according to the following formulas. The response distribution is the distribution specified (or chosen by default) through the DIST= option in the MODEL statement. The parameterizations used for log-likelihood functions of these distributions were chosen to facilitate expressions in terms of mean parameters that are modeled through an (inverse) link functions and in terms of scale parameters. These are not necessarily the parameterizations in which parameters of prior distributions are specified in a Bayesian analysis of homogeneous mixtures. See the section Prior Distributions for details about the parameterizations of prior distributions.
The HPFMM procedure includes all constant terms in the computation of densities or mass functions. In the expressions that
follow, l denotes the log-likelihood function,  denotes a general scale parameter,
denotes a general scale parameter, 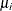 is the "mean", and
is the "mean", and 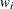 is a weight from the use of a WEIGHT
statement.
is a weight from the use of a WEIGHT
statement.
For some distributions (for example, the Weibull distribution) 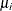 is not the mean of the distribution. The parameter
is not the mean of the distribution. The parameter 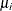 is the quantity that is modeled as
is the quantity that is modeled as 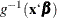 , where
, where 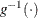 is the inverse link function and the
is the inverse link function and the  vector is constructed based on the effects in the MODEL
statement. Situations in which the parameter
vector is constructed based on the effects in the MODEL
statement. Situations in which the parameter 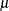 does not represent the mean of the distribution are explicitly mentioned in the list that follows.
does not represent the mean of the distribution are explicitly mentioned in the list that follows.
The parameter  is frequently labeled as a "Scale" parameter in output from the HPFMM procedure. It is not necessarily the scale parameter
of the particular distribution.
is frequently labeled as a "Scale" parameter in output from the HPFMM procedure. It is not necessarily the scale parameter
of the particular distribution.
- Beta
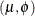
-
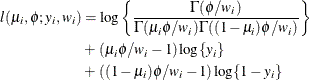
This parameterization of the beta distribution is due to Ferrari and Cribari-Neto (2004) and has properties
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) ,
, ![$\mr{Var}[Y] = \mu (1-\mu )/(1+\phi ), \, \phi > 0$](images/statug_hpfmm0182.png) .
.
- Beta-binomial
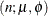
-
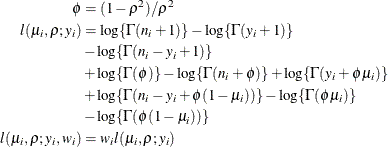
where
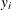 and
and 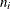 are the events and trials in the events/trials syntax and
are the events and trials in the events/trials syntax and 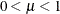 . This parameterization of the beta-binomial model presents the distribution as a special case of the Dirichlet-Multinomial
distribution—see, for example, Neerchal and Morel (1998). In this parameterization,
. This parameterization of the beta-binomial model presents the distribution as a special case of the Dirichlet-Multinomial
distribution—see, for example, Neerchal and Morel (1998). In this parameterization, ![$\mr{E}[Y] = n\mu $](images/statug_hpfmm0188.png) and
and ![$\mr{Var}[Y] = n\mu (1-\mu )(1+(n-1)/(\phi +1)), \, 0 \le \rho \le 1$](images/statug_hpfmm0189.png) . The HPFMM procedure models the parameter
. The HPFMM procedure models the parameter  and labels it "Scale" on the procedure output. For other parameterizations of the beta-binomial model, see Griffiths (1973) or Williams (1975).
and labels it "Scale" on the procedure output. For other parameterizations of the beta-binomial model, see Griffiths (1973) or Williams (1975).
- Binomial
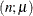
-
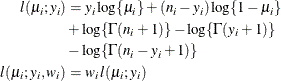
where
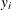 and
and 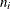 are the events and trials in the events/trials syntax and
are the events and trials in the events/trials syntax and 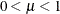 . In this parameterization
. In this parameterization ![$\mr{E}[Y] = n\mu $](images/statug_hpfmm0188.png) ,
, ![$\mr{Var}[Y] = n\mu (1-\mu )$](images/statug_hpfmm0192.png) .
.
- Binomial cluster
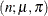
-
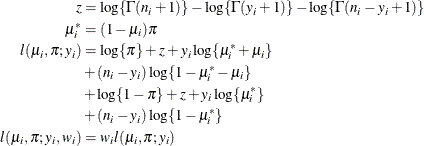
In this parameterization,
![$\mr{E}[Y] = n\pi $](images/statug_hpfmm0195.png) and
and ![$\mr{Var}[Y] = n\pi (1-\pi )\left\{ 1+\mu ^2(n-1)\right\} $](images/statug_hpfmm0196.png) . The binomial cluster model is a two-component mixture of a binomial
. The binomial cluster model is a two-component mixture of a binomial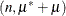 and a binomial
and a binomial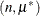 random variable. This mixture is unusual in that it fixes the number of components and because the mixing probability
random variable. This mixture is unusual in that it fixes the number of components and because the mixing probability  appears in the moments of the mixture components. For further details, see Morel and Nagaraj (1993); Morel and Neerchal (1997); Neerchal and Morel (1998) and Example 51.1 in this chapter. The expressions for the mean and variance in the binomial cluster model are identical to those of the beta-binomial
model shown previously, with
appears in the moments of the mixture components. For further details, see Morel and Nagaraj (1993); Morel and Neerchal (1997); Neerchal and Morel (1998) and Example 51.1 in this chapter. The expressions for the mean and variance in the binomial cluster model are identical to those of the beta-binomial
model shown previously, with 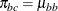 ,
, 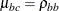 .
.
The HPFMM procedure models the parameter
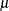 through the MODEL
statement and the parameter
through the MODEL
statement and the parameter  through the PROBMODEL
statement.
through the PROBMODEL
statement.
- Constant(c)
-
![\[ l(y_ i) = \left\{ \begin{array}{ll} 0 & y_ i = c \cr -1\mr{E}20 & y_ i \not= c \end{array}\right. \]](images/statug_hpfmm0201.png)
The extreme value when
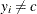 is chosen so that
is chosen so that 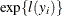 yields a likelihood of zero. You can change this value with the INVALIDLOGL=
option in the PROC HPFMM
statement. The constant distribution is useful for modeling overdispersion due to zero-inflation (or inflation of the process
at support c).
yields a likelihood of zero. You can change this value with the INVALIDLOGL=
option in the PROC HPFMM
statement. The constant distribution is useful for modeling overdispersion due to zero-inflation (or inflation of the process
at support c).
The DIST=CONSTANT distribution is useful for modeling an inflated probability of observing a particular value (zero, by default) in data from other discrete distributions, as demonstrated in Modeling Zero-Inflation: Is it Better to Fish Poorly or Not to Have Fished At All?. While it is syntactically valid to mix a constant distribution with a continuous distribution, such as DIST=LOGNORMAL, such a mixture is not mathematically appropriate, because the constant log-likelihood is the log of a probability, while a continuous log-likelihood is the log of a probability density function. If you want to mix a constant distribution with a continuous distribution, you could model the constant as a very narrow continuous distribution, such as DIST=UNIFORM(
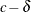 ,
, 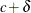 ) for a small value
) for a small value 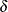 . However, using PROC HPFMM to analyze such mixtures is sensitive to numerical inaccuracy and ultimately unnecessary. Instead,
the following approach is mathematically equivalent and more numerically stable:
. However, using PROC HPFMM to analyze such mixtures is sensitive to numerical inaccuracy and ultimately unnecessary. Instead,
the following approach is mathematically equivalent and more numerically stable:
-
Estimate the mixing probability
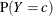 as the proportion of observations in the data set such that
as the proportion of observations in the data set such that 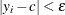 .
.
-
Estimate the parameters of the continuous distribution from the observations for which
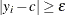 .
.
-
- Exponential
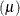
-
![\[ l(\mu _ i;y_ i,w_ i) = \left\{ \begin{array}{ll} -\log \{ \mu _ i\} - y_ i/\mu _ i & w_ i = 1 \cr w_ i\log \left\{ \frac{w_ iy_ i}{\mu _ i}\right\} - \frac{w_ iy_ i}{\mu _ i} - \log \{ y_ i \Gamma (w_ i)\} & w_ i \not= 1 \end{array} \right. \]](images/statug_hpfmm0211.png)
In this parameterization,
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) and
and ![$\mr{Var}[Y] = \mu ^2$](images/statug_hpfmm0212.png) .
.
- Folded normal
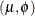
-
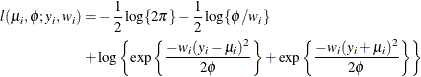
If X has a normal distribution with mean
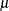 and variance
and variance  , then
, then 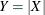 has a folded normal distribution and log-likelihood function
has a folded normal distribution and log-likelihood function 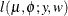 for
for 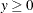 . The folded normal distribution arises, for example, when normally distributed measurements are observed, but their signs
are not observed. The mean and variance of the folded normal in terms of the underlying
. The folded normal distribution arises, for example, when normally distributed measurements are observed, but their signs
are not observed. The mean and variance of the folded normal in terms of the underlying 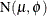 distribution are
distribution are
![\begin{align*} \mr{E}[Y] =& \frac{1}{\sqrt {2\pi \phi }} \exp \left\{ -\frac{\mu ^2}{2/\phi } \right\} + \mu \left(1-2\Phi \left(-\mu /\sqrt {\phi }\right)\right)\\ \mr{Var}[Y] =& \phi + \mu ^2 - \mr{E}[Y]^2 \end{align*}](images/statug_hpfmm0219.png)
The HPFMM procedure models the folded normal distribution through the mean
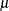 and variance
and variance  of the underlying normal distribution. When the HPFMM procedure computes output statistics for the response variable (for
example when you use the OUTPUT statement), the mean and variance of the response Y are reported. Similarly, the fit statistics apply to the distribution of
of the underlying normal distribution. When the HPFMM procedure computes output statistics for the response variable (for
example when you use the OUTPUT statement), the mean and variance of the response Y are reported. Similarly, the fit statistics apply to the distribution of 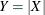 , not the distribution of X. When you model a folded normal variable, the response input variable should be positive; the HPFMM procedure treats negative
values of Y as a support violation.
, not the distribution of X. When you model a folded normal variable, the response input variable should be positive; the HPFMM procedure treats negative
values of Y as a support violation.
- Gamma
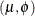
-
![\[ l(\mu _ i,\phi ;y_ i,w_ i) = w_ i\phi \log \left\{ \frac{w_ iy_ i\phi }{\mu _ i}\right\} - \frac{w_ iy_ i\phi }{\mu _ i} - \log \{ y_ i\} - \log \left\{ \Gamma (w_ i\phi )\right\} \]](images/statug_hpfmm0220.png)
In this parameterization,
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) and
and ![$\mr{Var}[Y] = \mu ^2/\phi , \, \phi > 0$](images/statug_hpfmm0221.png) . This parameterization of the gamma distribution differs from that in the GLIMMIX procedure, which expresses the log-likelihood
function in terms of
. This parameterization of the gamma distribution differs from that in the GLIMMIX procedure, which expresses the log-likelihood
function in terms of 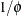 in order to achieve a variance function suitable for mixed model analysis.
in order to achieve a variance function suitable for mixed model analysis.
- Geometric
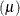
-
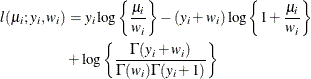
In this parameterization,
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) and
and ![$\mr{Var}[Y] = \mu + \mu ^2$](images/statug_hpfmm0224.png) . The geometric distribution is a special case of the negative binomial distribution with
. The geometric distribution is a special case of the negative binomial distribution with 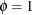 .
.
- Generalized Poisson
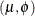
-

In this parameterization,
![$\mr{E}[Y]=\mu $](images/statug_hpfmm0227.png) ,
, ![$\mr{Var}[Y] = \mu /(1-\xi )^2,$](images/statug_hpfmm0228.png) and
and 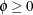 . The HPFMM procedure models the mean
. The HPFMM procedure models the mean 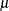 through the effects in the MODEL
statement and applies a log link by default. The generalized Poisson distribution provides an overdispersed alternative to
the Poisson distribution;
through the effects in the MODEL
statement and applies a log link by default. The generalized Poisson distribution provides an overdispersed alternative to
the Poisson distribution; 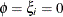 produces the mass function of a regular Poisson random variable. For details about the generalized Poisson distribution and
a comparison with the negative binomial distribution, see Joe and Zhu (2005).
produces the mass function of a regular Poisson random variable. For details about the generalized Poisson distribution and
a comparison with the negative binomial distribution, see Joe and Zhu (2005).
- Inverse Gaussian
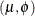
-
![\[ l(\mu _ i,\phi ;y_ i,w_ i) = -\frac{1}{2} \left[ \frac{w_ i(y_ i-\mu _ i)^2}{y_ i\phi \mu _ i^2} + \log \left\{ \frac{\phi y_ i^3}{w_ i} \right\} + \log \{ 2\pi \} \right] \]](images/statug_hpfmm0231.png)
The variance is
![$\mr{Var}[Y] = \phi \mu ^3, \, \phi > 0$](images/statug_hpfmm0232.png) .
.
- Lognormal
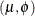
-
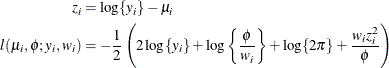
If
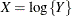 has a normal distribution with mean
has a normal distribution with mean 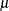 and variance
and variance  , then Y has the log-likelihood function
, then Y has the log-likelihood function 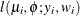 . The HPFMM procedure models the lognormal distribution and not the "shortcut" version you can obtain by taking the logarithm
of a random variable and modeling that as normally distributed. The two approaches are not equivalent, and the approach taken
by PROC HPFMM is the actual lognormal distribution. Although the lognormal model is a member of the exponential family of
distributions, it is not in the "natural" exponential family because it cannot be written in canonical form.
. The HPFMM procedure models the lognormal distribution and not the "shortcut" version you can obtain by taking the logarithm
of a random variable and modeling that as normally distributed. The two approaches are not equivalent, and the approach taken
by PROC HPFMM is the actual lognormal distribution. Although the lognormal model is a member of the exponential family of
distributions, it is not in the "natural" exponential family because it cannot be written in canonical form.
In terms of the parameters
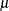 and
and  of the underlying normal process for X, the mean and variance of Y are
of the underlying normal process for X, the mean and variance of Y are ![$\mr{E}[Y] = \exp \{ \mu \} \sqrt {\omega }$](images/statug_hpfmm0236.png) and
and ![$\mr{Var}[Y] = \exp \{ 2\mu \} \omega (\omega -1)$](images/statug_hpfmm0237.png) , respectively, where
, respectively, where 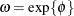 . When you request predicted values with the OUTPUT
statement, the HPFMM procedure computes
. When you request predicted values with the OUTPUT
statement, the HPFMM procedure computes ![$\mr{E}[Y]$](images/statug_hpfmm0239.png) and not
and not 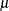 .
.
- Negative binomial
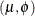
-
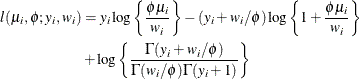
The variance is
![$\mr{Var}[Y] = \mu + \phi \mu ^2, \, \phi > 0$](images/statug_hpfmm0241.png) .
.
For a given
 , the negative binomial distribution is a member of the exponential family. The parameter
, the negative binomial distribution is a member of the exponential family. The parameter  is related to the scale of the data because it is part of the variance function. However, it cannot be factored from the
variance, as is the case with the
is related to the scale of the data because it is part of the variance function. However, it cannot be factored from the
variance, as is the case with the  parameter in many other distributions.
parameter in many other distributions.
- Normal
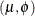
-
![\[ l(\mu _ i,\phi ;y_ i,w_ i) = -\frac{1}{2} \left[ \frac{w_ i(y_ i-\mu _ i)^2}{\phi } + \log \left\{ \frac{\phi }{w_ i}\right\} + \log \{ 2\pi \} \right] \]](images/statug_hpfmm0242.png)
The mean and variance are
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) and
and ![$\mr{Var}[Y] = \phi $](images/statug_hpfmm0243.png) , respectively,
, respectively, 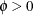
- Poisson
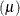
-
![\[ l(\mu _ i;y_ i,w_ i) = w_ i (y_ i \log \{ \mu _ i\} - \mu _ i - \log \{ \Gamma (y_ i + 1)\} ) \]](images/statug_hpfmm0244.png)
The mean and variance are
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) and
and ![$\mr{Var}[Y] = \mu $](images/statug_hpfmm0245.png) .
.
- (Shifted) T
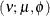
-
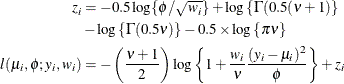
In this parameterization
![$\mr{E}[Y] = \mu $](images/statug_hpfmm0181.png) and
and ![$\mr{Var}[Y] = \phi \nu /(\nu -2), \, \phi > 0, \nu > 0$](images/statug_hpfmm0248.png) . Note that this form of the t distribution is not a non-central distribution, but that of a shifted central t random variable.
. Note that this form of the t distribution is not a non-central distribution, but that of a shifted central t random variable.
- Truncated Exponential
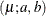
-
![\begin{align*} l(\mu _ i; a, b, y_ i, w_ i) & = w_ i\log \left\{ \frac{w_ iy_ i}{\mu _ i}\right\} - \frac{w_ iy_ i}{\mu _ i} - \log \{ y_ i \Gamma (w_ i)\} \\ & - \log \left[ \frac{\gamma \left(w_ i, \frac{w_ i b}{\mu _ i} \right)}{\Gamma (w_ i)} - \frac{\gamma \left(w_ i, \frac{w_ i a}{\mu _ i} \right)}{\Gamma (w_ i)} \right] \end{align*}](images/statug_hpfmm0250.png)
where
![\[ \gamma (c_1, c_2) = \int _0^{c_2} t^{c_1-1} \exp (-t) \mr{d}t \]](images/statug_hpfmm0251.png)
is the lower incomplete gamma function. The mean and variance are
![\begin{align*} \mr{E}[Y] & = \frac{(a+\mu _ i) \exp (-a/\mu _ i) - (b+\mu _ i) \exp (-b/\mu _ i)}{\exp (-a/\mu _ i) - \exp (-b/\mu _ i)} \\ \mr{Var}[Y] & = \frac{(a^2+2a\mu _ i+2\mu _ i^2) \exp (-a/\mu _ i) - (b^2+2b\mu _ i+2\mu _ i^2) \exp (-b/\mu _ i)}{\exp (-a/\mu _ i) - \exp (-b/\mu _ i)} \\ & - \left(\mr{E}[Y] \right)^2 \end{align*}](images/statug_hpfmm0252.png)
- Truncated Lognormal
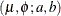
-
![\begin{align*} z_ i & = \log \{ y_ i\} - \mu _ i \\ l(\mu _ i, \phi ; a, b, y_ i, w_ i) & = -\frac{1}{2}\left( 2\log \{ y_ i\} + \log \left\{ \frac{\phi }{w_ i} \right\} + \log \{ 2\pi \} + \frac{w_ i z_ i^2}{\phi } \right) \\ & - \log \left\{ \Phi \left[ \sqrt {w_ i/\phi }(\log b - \mu _ i) \right] - \Phi \left[ \sqrt {w_ i/\phi }(\log a - \mu _ i) \right]\right\} \end{align*}](images/statug_hpfmm0254.png)
where
 is the cumulative distribution function of the standard normal distribution. The mean and variance are
is the cumulative distribution function of the standard normal distribution. The mean and variance are
![\begin{align*} \mr{E}[Y] & = \exp (\mu _ i + 0.5\phi ) \frac{\Phi \left(\sqrt {\phi } - \frac{\log a - \mu _ i}{\sqrt {\phi }} \right) - \Phi \left(\sqrt {\phi } - \frac{\log b - \mu _ i}{\sqrt {\phi }} \right)}{\Phi \left(\frac{\log b - \mu _ i}{\sqrt {\phi }} \right) - \Phi \left(\frac{\log a - \mu _ i}{\sqrt {\phi }} \right)} \\ \mr{Var}[Y] & = \exp (2\mu _ i + 2\phi ) \frac{\Phi \left(2\sqrt {\phi } - \frac{\log a - \mu _ i}{\sqrt {\phi }} \right) - \Phi \left(2\sqrt {\phi } - \frac{\log b - \mu _ i}{\sqrt {\phi }} \right)}{\Phi \left(\frac{\log b - \mu _ i}{\sqrt {\phi }} \right) - \Phi \left(\frac{\log a - \mu _ i}{\sqrt {\phi }} \right)} - \left(\mr{E}[Y] \right)^2 \end{align*}](images/statug_hpfmm0256.png)
- Truncated Negative binomial
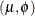
-
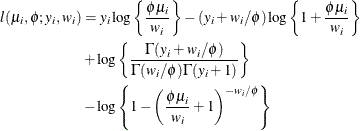
The mean and variance are
![\begin{align*} \mr{E}[Y] & = \mu _ i \left\{ 1 - (\phi \mu _ i + 1)^{-1/\phi } \right\} ^{-1} \\ \mr{Var}[Y] & = (1 + \phi \mu _ i + \mu _ i) \mr{E}[Y] - \left(\mr{E}[Y] \right)^2 \end{align*}](images/statug_hpfmm0258.png)
- Truncated Normal
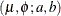
-
![\begin{align*} l(\mu _ i, \phi ; a, b, y_ i, w_ i) & = -\frac{1}{2} \left[ \frac{w_ i(y_ i-\mu _ i)^2}{\phi } + \log \left\{ \frac{\phi }{w_ i}\right\} + \log \{ 2\pi \} \right] \\ & - \log \left\{ \Phi \left[ \sqrt {w_ i/\phi }(b-\mu _ i) \right] - \Phi \left[ \sqrt {w_ i/\phi }(a-\mu _ i) \right]\right\} \end{align*}](images/statug_hpfmm0259.png)
where
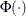 is the cumulative distribution function of the standard normal distribution. The mean and variance are
is the cumulative distribution function of the standard normal distribution. The mean and variance are
![\begin{align*} \mr{E}[Y] & = \mu _ i + \sqrt {\phi } \frac{\mr{phi}\left(\frac{a-\mu _ i}{\sqrt {\phi }} \right) - \mr{phi}\left(\frac{b-\mu _ i}{\sqrt {\phi }} \right)}{\Phi \left(\frac{b-\mu _ i}{\sqrt {\phi }} \right) - \Phi \left(\frac{a-\mu _ i}{\sqrt {\phi }} \right)}\\ \mr{Var}[Y] & = \phi \left[1 + \frac{\frac{a-\mu _ i}{\sqrt {\phi }} \mr{phi}\left(\frac{a-\mu _ i}{\sqrt {\phi }} \right) - \frac{b-\mu _ i}{\sqrt {\phi }} \mr{phi}\left(\frac{b-\mu _ i}{\sqrt {\phi }} \right)}{\Phi \left(\frac{b-\mu _ i}{\sqrt {\phi }} \right) - \Phi \left(\frac{a-\mu _ i}{\sqrt {\phi }} \right)} \right. \\ & - \left. \left\{ \frac{\mr{phi}\left(\frac{a-\mu _ i}{\sqrt {\phi }} \right) - \mr{phi}\left(\frac{b-\mu _ i}{\sqrt {\phi }} \right)}{\Phi \left(\frac{b-\mu _ i}{\sqrt {\phi }} \right) - \Phi \left(\frac{a-\mu _ i}{\sqrt {\phi }} \right)}\right\} ^2 \right] \end{align*}](images/statug_hpfmm0260.png)
where
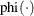 is the probability density function of the standard normal distribution.
is the probability density function of the standard normal distribution.
- Truncated Poisson
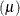
-
![\[ l(\mu _ i;y_ i,w_ i) = w_ i (y_ i \log \{ \mu _ i\} - \log \{ \exp (\mu _ i) - 1\} - \log \{ \Gamma (y_ i + 1)\} ) \]](images/statug_hpfmm0262.png)
The mean and variance are
![\begin{align*} \mr{E}[Y] & = \frac{\mu }{1-\exp (-\mu _ i)} \\ \mr{Var}[Y] & = \frac{\mu _ i \left[1 - \exp (-\mu _ i) - \mu _ i \exp (-\mu _ i)\right]}{[1-\exp (-\mu _ i)]^2} \end{align*}](images/statug_hpfmm0263.png)
- Uniform
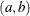
-
![\[ l(\mu _ i;y_ i,w_ i) = -\log \{ b-a\} \]](images/statug_hpfmm0264.png)
The mean and variance are
![$\mr{E}[Y] = 0.5(a+b)$](images/statug_hpfmm0265.png) and
and ![$\mr{Var}[Y] = (b-a)^2/12$](images/statug_hpfmm0266.png) .
.
- Weibull
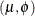
-
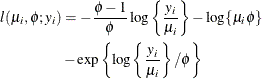
In this particular parameterization of the two-parameter Weibull distribution, the mean and variance of the random variable Y are
![$\mr{E}[Y] = \mu \Gamma (1+\phi )$](images/statug_hpfmm0268.png) and
and ![$\mr{Var}[Y] = \mu ^2\left\{ \Gamma (1+2\phi ) - \Gamma ^2(1+\phi ) \right\} $](images/statug_hpfmm0269.png) .
.
