The FREQ Procedure

Gail-Simon Test for Qualitative Interactions

The GAILSIMON option in the TABLES statement provides the Gail-Simon test for qualitative interaction for stratified 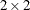$2 \times 2$ tables. For more information, see Gail and Simon (1985); Silvapulle (2001); Dmitrienko et al. (2005).

The Gail-Simon test is based on the risk differences in stratified 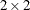$2 \times 2$ tables, where the risk difference is defined as the row 1 risk (proportion in column 1) minus the row 2 risk. For more information, see the section Risks and Risk Differences. By default, PROC FREQ uses column 1 risks to compute the Gail-Simon test. If you specify the GAILSIMON(COLUMN=2) option, PROC FREQ uses column 2 risks.

PROC FREQ computes the Gail-Simon test statistics as described in Gail and Simon (1985),

$\begin{eqnarray*} Q- & =& \sum _ h ~ (d_ h / s_ h)^2 ~ I(d_ h > 0 ) \\[0.10in] Q+ & =& \sum _ h ~ (d_ h / s_ h)^2 ~ I( d_ h < 0 ) \\[0.10in] Q & =& \min ~ (Q-, ~ Q+) \end{eqnarray*}$

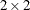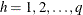where $d_ h$ is the risk difference in table h, $s_ h$ is the standard error of the risk difference, and $I(d_ h > 0)$ equals 1 if $d_ h > 0$ and 0 otherwise. Similarly, $I(d_ h < 0)$ equals 1 if $d_ h < 0$ and 0 otherwise. The q $2 \times 2$ tables (strata) are indexed by $h = 1, 2, \ldots , q$ .

The p-values for the Gail-Simon statistics are computed as

$\begin{eqnarray*} p(Q-) & =& \sum _ h ~ (1 - F_ h(Q-)) ~ B(h; n=q, p=0.5) \\[0.10in] p(Q+) & =& \sum _ h ~ (1 - F_ h(Q+)) ~ B(h; n=q, p=0.5) \\[0.10in] p(Q) & =& \sum _{h=1}^{q-1} ~ (1-F_ h(Q)) ~ B(h; n=(q-1), p=0.5) \end{eqnarray*}$

where $F_ h(\cdot )$ is the cumulative chi-square distribution function with h degrees of freedom and $B(h; n, p)$ is the binomial probability function with parameters n and p. The statistic Q tests the null hypothesis of no qualitative interaction. The statistic $Q-$ tests the null hypothesis of positive risk differences. A small p-value for $Q-$ indicates negative differences; similarly, a small p-value for $Q+$ indicates positive risk differences.