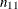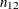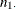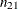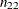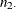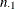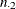The FREQ Procedure
Risks and Risk Differences
The RISKDIFF option in the TABLES statement provides estimates of risks (binomial proportions) and risk differences for 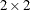 tables. This analysis might be appropriate when comparing the proportion of some characteristic for two groups, where row
1 and row 2 correspond to the two groups, and the columns correspond to two possible characteristics or outcomes. For example,
the row variable might be a treatment or dose, and the column variable might be the response. For more information, see Collett
(1991); Fleiss, Levin, and Paik (2003); Stokes, Davis, and Koch (2012).
tables. This analysis might be appropriate when comparing the proportion of some characteristic for two groups, where row
1 and row 2 correspond to the two groups, and the columns correspond to two possible characteristics or outcomes. For example,
the row variable might be a treatment or dose, and the column variable might be the response. For more information, see Collett
(1991); Fleiss, Levin, and Paik (2003); Stokes, Davis, and Koch (2012).
Let the frequencies of the 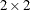 table be represented as follows.
table be represented as follows.
|
Column 1 |
Column 2 |
Total |
|
|
Row 1 |
|
|
|
|
Row 2 |
|
|
|
|
Total |
|
|
n |
By default when you specify the RISKDIFF option, PROC FREQ provides estimates of the row 1 risk (proportion), the row 2 risk,
the overall risk, and the risk difference for column 1 and for column 2 of the 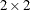 table. The risk difference is defined as the row 1 risk minus the row 2 risk. The risks are binomial proportions of their
rows (row 1, row 2, or overall), and the computation of their standard errors and Wald confidence limits follow the binomial
proportion computations, which are described in the section Binomial Proportion.
table. The risk difference is defined as the row 1 risk minus the row 2 risk. The risks are binomial proportions of their
rows (row 1, row 2, or overall), and the computation of their standard errors and Wald confidence limits follow the binomial
proportion computations, which are described in the section Binomial Proportion.
The column 1 risk for row 1 is the proportion of row 1 observations classified in column 1,
![\[ \hat{p}_1 = n_{11} ~ / ~ n_{1 \cdot } \]](images/statug_freq0282.png)
which estimates the conditional probability of the column 1 response, given the first level of the row variable. The column 1 risk for row 2 is the proportion of row 2 observations classified in column 1,
![\[ \hat{p}_2 = n_{21} ~ / ~ n_{2 \cdot } \]](images/statug_freq0283.png)
The overall column 1 risk is the proportion of all observations classified in column 1,
![\[ \hat{p} = n_{\cdot 1} ~ / ~ n \]](images/statug_freq0284.png)
The column 1 risk difference compares the risks for the two rows, and it is computed as the column 1 risk for row 1 minus the column 1 risk for row 2,
![\[ \hat{d} = \hat{p}_1 - \hat{p}_2 \]](images/statug_freq0285.png)
The standard error of the column 1 risk for row i is computed as
![\[ \mr{se}(\hat{p}_ i) = \sqrt { \hat{p}_ i ~ ( 1 - \hat{p}_ i ) ~ / ~ n_{i \cdot } } \]](images/statug_freq0286.png)
The standard error of the overall column 1 risk is computed as
![\[ \mr{se}(\hat{p}) = \sqrt { \hat{p} ~ ( 1 - \hat{p} ) ~ / ~ n } \]](images/statug_freq0287.png)
Where the two rows represent independent binomial samples, the standard error of the column 1 risk difference is computed as
![\[ \mr{se}(\hat{d}) = \sqrt { \hat{p}_1 (1 - \hat{p}_1) / n_{1 \cdot } ~ + ~ \hat{p}_2 (1 - \hat{p}_2) / n_{2 \cdot }} \]](images/statug_freq0288.png)
The computations are similar for the column 2 risks and risk difference.
Confidence Limits
By default, the RISKDIFF option provides Wald asymptotic confidence limits for the risks (row 1, row 2, and overall) and the risk difference. By default, the RISKDIFF option also provides exact (Clopper-Pearson) confidence limits for the risks. You can suppress the display of this information by specifying the NORISKS riskdiff-option. You can specify riskdiff-options to request tests and other types of confidence limits for the risk difference. For more information, see the sections Confidence Limits for the Risk Difference and Risk Difference Tests.
The risks are equivalent to the binomial proportions of their corresponding rows. This section describes the Wald confidence limits that are provided by default when you specify the RISKDIFF option. The BINOMIAL option provides additional confidence limit types and tests for risks (binomial proportions). For more information, see the sections Binomial Confidence Limits and Binomial Tests.
The Wald confidence limits are based on the normal approximation to the binomial distribution. PROC FREQ computes the Wald confidence limits for the risks and risk differences as
![\[ \mr{Est} ~ \pm ~ (~ z_{\alpha /2} \times \mr{se}(\mr{Est}) ~ ) \]](images/statug_freq0289.png)
where Est is the estimate, 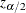 is the
is the 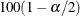 th percentile of the standard normal distribution, and
th percentile of the standard normal distribution, and 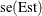 is the standard error of the estimate. The confidence level
is the standard error of the estimate. The confidence level  is determined by the value of the ALPHA= option; by default, ALPHA=0.05, which produces 95% confidence limits.
is determined by the value of the ALPHA= option; by default, ALPHA=0.05, which produces 95% confidence limits.
If you specify the CORRECT riskdiff-option, PROC FREQ includes continuity corrections in the Wald confidence limits for the risks and risk differences. The purpose of a continuity correction is to adjust for the difference between the normal approximation and the binomial distribution, which is discrete. See Fleiss, Levin, and Paik (2003) for more information. The continuity-corrected Wald confidence limits are computed as
![\[ \mr{Est} ~ \pm ~ (~ z_{\alpha /2} \times \mr{se}(\mr{Est}) + \mathit{cc} ~ ) \]](images/statug_freq0291.png)
where cc is the continuity correction. For the row 1 risk, 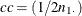 ; for the row 2 risk,
; for the row 2 risk, 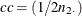 ; for the overall risk,
; for the overall risk, 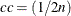 ; and for the risk difference,
; and for the risk difference, 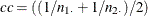 . The column 1 and column 2 risks use the same continuity corrections.
. The column 1 and column 2 risks use the same continuity corrections.
By default when you specify the RISKDIFF option, PROC FREQ also provides exact (Clopper-Pearson) confidence limits for the column 1, column 2, and overall risks. These confidence limits are constructed by inverting the equal-tailed test that is based on the binomial distribution. For more information, see the section Exact (Clopper-Pearson) Confidence Limits.
Confidence Limits for the Risk Difference
PROC FREQ provides the following confidence limit types for the risk difference: Agresti-Caffo, exact unconditional, Hauck-Anderson, Miettinen-Nurminen (score), Newcombe (hybrid-score), and Wald confidence limits. Continuity-corrected forms of Newcombe and Wald confidence limits are also available.
The confidence coefficient for the confidence limits produced by the CL= riskdiff-option is 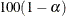 %, where the value of
%, where the value of  is determined by the ALPHA= option. By default, ALPHA=0.05, which produces 95% confidence limits. This differs from the test-based
confidence limits that are provided with the equivalence, noninferiority, and superiority tests, which have a confidence coefficient
of
is determined by the ALPHA= option. By default, ALPHA=0.05, which produces 95% confidence limits. This differs from the test-based
confidence limits that are provided with the equivalence, noninferiority, and superiority tests, which have a confidence coefficient
of 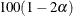 % (Schuirmann 1999). For more information, see the section Risk Difference Tests.
% (Schuirmann 1999). For more information, see the section Risk Difference Tests.
Agresti-Caffo Confidence Limits
Agresti-Caffo confidence limits for the risk difference are computed as
![\[ \tilde{d} ~ \pm ~ ( ~ z_{\alpha /2} \times \mr{se}(\tilde{d}) ~ ) \]](images/statug_freq0296.png)
where 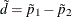 ,
, 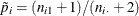 ,
,
![\[ \mr{se}(\tilde{d}) = \sqrt { \tilde{p}_1 ( 1 - \tilde{p}_2 ) / ( n_{1 \cdot } + 2 ) ~ + ~ \tilde{p}_2 ( 1 - \tilde{p}_2 ) / ( n_{2 \cdot } + 2 ) } \]](images/statug_freq0299.png)
and 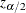 is the
is the 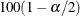 th percentile of the standard normal distribution.
th percentile of the standard normal distribution.
The Agresti-Caffo interval adjusts the Wald interval for the risk difference by adding a pseudo-observation of each type (success and failure) to each sample. See Agresti and Caffo (2000) and Agresti and Coull (1998) for more information.
Hauck-Anderson Confidence Limits
Hauck-Anderson confidence limits for the risk difference are computed as
![\[ \hat{d} ~ \pm ~ ( ~ \mathit{cc} ~ + ~ z_{\alpha /2} \times \mr{se}(\hat{d}) ~ ) \]](images/statug_freq0300.png)
where 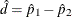 and
and 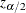 is the
is the 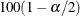 th percentile of the standard normal distribution. The standard error is computed from the sample proportions as
th percentile of the standard normal distribution. The standard error is computed from the sample proportions as
![\[ \mr{se}(\hat{d}) = \sqrt { \hat{p}_1 (1-\hat{p}_1) / (n_{1 \cdot }-1) ~ +~ \hat{p}_2 (1-\hat{p}_2) / (n_{2 \cdot }-1) } \]](images/statug_freq0302.png)
The Hauck-Anderson continuity correction cc is computed as
![\[ \mathit{cc} = 1 ~ / ~ \bigl ( 2 ~ \min ( n_{1 \cdot }, ~ n_{2 \cdot } ) \bigr ) \]](images/statug_freq0303.png)
See Hauck and Anderson (1986) for more information. The subsection "Hauck-Anderson Test" in the section Noninferiority Tests describes the corresponding noninferiority test.
Miettinen-Nurminen (Score) Confidence Limits
Miettinen-Nurminen (score) confidence limits for the risk difference (Miettinen and Nurminen 1985) are computed by inverting score tests for the risk difference. A score-based test statistic for the null hypothesis that
the risk difference equals  can be expressed as
can be expressed as
![\[ T(\delta ) = ( \hat{d} - \delta ) / \sqrt { \widetilde{\mr{Var}}(\delta }) \]](images/statug_freq0304.png)
where 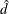 is the observed value of the risk difference (
is the observed value of the risk difference (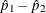 ),
),
![\[ \widetilde{\mr{Var}}(\delta ) = \left( n / (n-1) \right) ~ \left( ~ \tilde{p}_1(\delta ) ( 1 - \tilde{p}_1(\delta ) ) / n_1 + \tilde{p}_2(\delta ) ( 1 - \tilde{p}_2(\delta ) ) / n_2 ~ \right) \]](images/statug_freq0307.png)
and 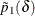 and
and 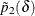 are the maximum likelihood estimates of the row 1 and row 2 risks (proportions) under the restriction that the risk difference
is
are the maximum likelihood estimates of the row 1 and row 2 risks (proportions) under the restriction that the risk difference
is  . For more information, see Miettinen and Nurminen (1985, pp. 215–216) and Miettinen (1985, chapter 12).
. For more information, see Miettinen and Nurminen (1985, pp. 215–216) and Miettinen (1985, chapter 12).
The 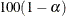 % confidence interval for the risk difference consists of all values of
% confidence interval for the risk difference consists of all values of  for which the score test statistic
for which the score test statistic 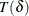 falls in the acceptance region,
falls in the acceptance region,
![\[ \{ \delta : T(\delta ) < z_{\alpha /2} \} \]](images/statug_freq0311.png)
where 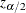 is the
is the 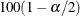 th percentile of the standard normal distribution. PROC FREQ finds the confidence limits by iterative computation, which stops
when the iteration increment falls below the convergence criterion or when the maximum number of iterations is reached, whichever
occurs first. By default, the convergence criterion is 0.00000001 and the maximum number of iterations is 100.
th percentile of the standard normal distribution. PROC FREQ finds the confidence limits by iterative computation, which stops
when the iteration increment falls below the convergence criterion or when the maximum number of iterations is reached, whichever
occurs first. By default, the convergence criterion is 0.00000001 and the maximum number of iterations is 100.
By default, the Miettinen-Nurminen confidence limits include the bias correction factor 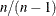 in the computation of
in the computation of 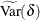 (Miettinen and Nurminen 1985, p. 216). For more information, see Newcombe and Nurminen (2011). If you specify the CL=MN(CORRECT=NO) riskdiff-option, PROC FREQ does not include the bias correction factor in this computation (Mee 1984). See also Agresti (2002, p. 77). The uncorrected confidence limits are labeled as "Miettinen-Nurminen-Mee" confidence limits in the displayed output.
(Miettinen and Nurminen 1985, p. 216). For more information, see Newcombe and Nurminen (2011). If you specify the CL=MN(CORRECT=NO) riskdiff-option, PROC FREQ does not include the bias correction factor in this computation (Mee 1984). See also Agresti (2002, p. 77). The uncorrected confidence limits are labeled as "Miettinen-Nurminen-Mee" confidence limits in the displayed output.
The maximum likelihood estimates of 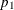 and
and 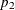 , subject to the constraint that the risk difference is
, subject to the constraint that the risk difference is  , are computed as
, are computed as
![\[ \tilde{p}_1 = 2 u \cos (w) - b/3a \hspace{.15in} \mr{and} \hspace{.15in} \tilde{p}_2 = \tilde{p}_1 + \delta \]](images/statug_freq0316.png)
where
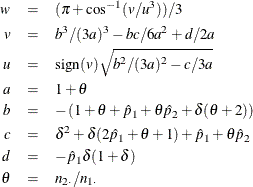
For more information, see Farrington and Manning (1990, p. 1453).
Newcombe Confidence Limits
Newcombe (hybrid-score) confidence limits for the risk difference are constructed from the Wilson score confidence limits
for each of the two individual proportions. The confidence limits for the individual proportions are used in the standard
error terms of the Wald confidence limits for the proportion difference. See Newcombe (1998a) and Barker et al. (2001) for more information.
Wilson score confidence limits for 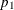 and
and 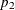 are the roots of
are the roots of
![\[ | p_ i - \hat{p}_ i | = z_{\alpha /2} \sqrt { p_ i (1-p_ i)/n_{i \cdot } } \]](images/statug_freq0318.png)
for 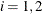 . The confidence limits are computed as
. The confidence limits are computed as
![\[ \left( \hat{p}_ i ~ + ~ z_{\alpha /2}^2/2n_{i \cdot } ~ \pm ~ z_{\alpha /2} \sqrt { \left( \hat{p}_ i (1-\hat{p}_ i) + z_{\alpha }^2 / 4n_{i \cdot } \right) / n_{i \cdot } } ~ \right) ~ / ~ \left( 1 + z_{\alpha /2}^2 / n_{i \cdot } \right) \]](images/statug_freq0320.png)
For more information, see the section Wilson (Score) Confidence Limits.
Denote the lower and upper Wilson score confidence limits for 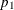 as
as 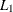 and
and 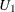 , and denote the lower and upper confidence limits for
, and denote the lower and upper confidence limits for 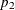 as
as 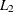 and
and 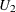 . The Newcombe confidence limits for the proportion difference (
. The Newcombe confidence limits for the proportion difference (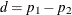 ) are computed as
) are computed as
![\begin{eqnarray*} d_ L = (\hat{p}_1 - \hat{p}_2) ~ - ~ \sqrt { ( \hat{p}_1 - L_1 )^2 ~ +~ ( U_2 - \hat{p}_2 )^2 } \\[0.10in] d_ U = (\hat{p}_1 - \hat{p}_2) ~ + ~ \sqrt { ( U_1 - \hat{p}_1 )^2 ~ +~ ( \hat{p}_2 - L_2 )^2 } \end{eqnarray*}](images/statug_freq0325.png)
If you specify the CORRECT riskdiff-option, PROC FREQ provides continuity-corrected Newcombe confidence limits. By including a continuity correction of 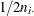 , the Wilson score confidence limits for the individual proportions are computed as the roots of
, the Wilson score confidence limits for the individual proportions are computed as the roots of
![\[ | p_ i - \hat{p}_ i | - 1/2n_{i \cdot } = z_{\alpha /2} \sqrt { p_ i (1-p_ i)/n_{i \cdot } } \]](images/statug_freq0327.png)
The continuity-corrected confidence limits for the individual proportions are then used to compute the proportion difference
confidence limits 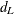 and
and 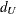 .
.
Wald Confidence Limits
Wald confidence limits for the risk difference are computed as
![\[ \hat{d} ~ \pm ~ ( ~ z_{\alpha /2} \times \mr{se}(\hat{d}) ~ ) \]](images/statug_freq0330.png)
where 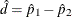 ,
, 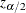 is the
is the 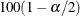 th percentile of the standard normal distribution. and the standard error is computed from the sample proportions as
th percentile of the standard normal distribution. and the standard error is computed from the sample proportions as
![\[ \mr{se}(\hat{d}) = \sqrt { \hat{p}_1 (1-\hat{p}_1) / n_{1 \cdot } ~ +~ \hat{p}_2 (1-\hat{p}_2) / n_{2 \cdot } } \]](images/statug_freq0331.png)
If you specify the CORRECT riskdiff-option, the Wald confidence limits include a continuity correction cc,
![\[ \hat{d} ~ \pm ~ ( ~ \mathit{cc} ~ + ~ z_{\alpha /2} \times \mr{se}(\hat{d}) ~ ) \]](images/statug_freq0300.png)
where 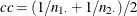 .
.
The subsection "Wald Test" in the section Noninferiority Tests describes the corresponding noninferiority test.
Exact Unconditional Confidence Limits
If you specify the RISKDIFF option in the EXACT statement, PROC FREQ provides exact unconditional confidence limits for the
risk difference. PROC FREQ computes the confidence limits by inverting two separate one-sided tests (tail method), where the
size of each test is at most 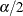 and the confidence coefficient is at least
and the confidence coefficient is at least 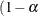 ). The conditional exact method, which is described in the section Exact Statistics, does not apply to the risk difference because of a nuisance parameter (Agresti 1992). The unconditional method (which fixes only the row margins) eliminates the nuisance parameter by maximizing the p-value over all possible values of the parameter (Santner and Snell 1980).
). The conditional exact method, which is described in the section Exact Statistics, does not apply to the risk difference because of a nuisance parameter (Agresti 1992). The unconditional method (which fixes only the row margins) eliminates the nuisance parameter by maximizing the p-value over all possible values of the parameter (Santner and Snell 1980).
By default, PROC FREQ uses the unstandardized risk difference as the test statistic to compute the confidence limits. If you specify the RISKDIFF(METHOD=SCORE) option, the procedure uses the score statistic to compute the confidence limits (Chan and Zhang 1999). The score statistic is a less discrete statistic than the unstandardized risk difference and produces less conservative confidence limits (Agresti and Min 2001). For more information, see Santner et al. (2007). The section Confidence Limits for the Risk Difference describes the computation of the risk difference score statistic. For more information, see Miettinen and Nurminen (1985) and Farrington and Manning (1990).
PROC FREQ computes the exact unconditional confidence limits as follows. The risk difference is defined as the difference
between the row 1 and row 2 risks (proportions), 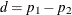 , and
, and 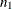 and
and 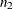 denote the row totals of the
denote the row totals of the 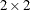 table. The joint probability function for the table can be expressed in terms of the table cell frequencies, the risk difference,
and the nuisance parameter
table. The joint probability function for the table can be expressed in terms of the table cell frequencies, the risk difference,
and the nuisance parameter 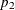 as
as
![\[ f( n_{11}, n_{21}; n_1, n_2, d, p_2 ) = \binom {n_1}{n_{11}} (d + p_2)^{n_{11}} (1-d-p_2)^{n_1-n_{11}} \times \binom {n_2}{n_{21}} p_2^{n_{21}} (1-p_2)^{n_2 - n_{21}} \]](images/statug_freq0335.png)
The 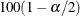 % confidence limits for the risk difference are computed as
% confidence limits for the risk difference are computed as
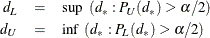
where
![\begin{eqnarray*} P_ U(d_\ast ) & = & \sup _{p_2} ~ \bigl ( \sum _{A, T(a) \geq t_0} f( n_{11}, n_{21}; n_1, n_2, d_\ast , p_2 ) ~ \bigr ) \\[0.10in] P_ L(d_\ast ) & = & \sup _{p_2} ~ \bigl ( \sum _{A, T(a) \leq t_0} f( n_{11}, n_{21}; n_1, n_2, d_\ast , p_2 ) ~ \bigr ) \end{eqnarray*}](images/statug_freq0337.png)
The set A includes all 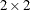 tables with row sums equal to
tables with row sums equal to  and
and 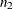 , and
, and 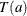 denotes the value of the test statistic for table a in A. To compute
denotes the value of the test statistic for table a in A. To compute 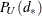 , the sum includes probabilities of those tables for which (
, the sum includes probabilities of those tables for which (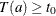 ), where
), where 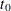 is the value of the test statistic for the observed table. For a fixed value of
is the value of the test statistic for the observed table. For a fixed value of 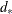 ,
, 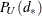 is taken to be the maximum sum over all possible values of
is taken to be the maximum sum over all possible values of 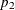 .
.
Risk Difference Tests
PROC FREQ provides tests of equality, noninferiority, superiority, and equivalence for the risk (proportion) difference. The following analysis methods are available: Wald (with and without continuity correction), Hauck-Anderson, Farrington-Manning (score), and Newcombe (with and without continuity correction). You can specify the method by using the METHOD= riskdiff-option; by default, PROC FREQ provides Wald tests.
Equality Tests
The equality test for the risk difference tests the null hypothesis that the risk difference equals the null value. You can
specify a null value by using the EQUAL(NULL=) riskdiff-option; by default, the null value is 0. This test can be expressed as 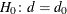 versus the alternative
versus the alternative 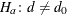 , where
, where 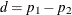 denotes the risk difference (for column 1 or column 2) and
denotes the risk difference (for column 1 or column 2) and 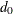 denotes the null value.
denotes the null value.
The test statistic is computed as
![\[ z = (\hat{d} - d_0) / \mr{se}(\hat{d}) \]](images/statug_freq0346.png)
where the standard error 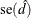 is computed by using the method that you specify. Available methods for the equality test include Wald (with and without
continuity correction), Hauck-Anderson, and Farrington-Manning (score). For a description of the standard error computation,
see the subsections "Wald Test,"
"Hauck-Anderson Test,"
and "Farrington-Manning (Score) Test,"
respectively, in the section Noninferiority Tests.
is computed by using the method that you specify. Available methods for the equality test include Wald (with and without
continuity correction), Hauck-Anderson, and Farrington-Manning (score). For a description of the standard error computation,
see the subsections "Wald Test,"
"Hauck-Anderson Test,"
and "Farrington-Manning (Score) Test,"
respectively, in the section Noninferiority Tests.
PROC FREQ computes one-sided and two-sided p-values for equality tests. When the test statistic z is greater than 0, PROC FREQ displays the right-sided p-value, which is the probability of a larger value occurring under the null hypothesis. The one-sided p-value can be expressed as
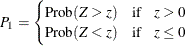
where Z has a standard normal distribution. The two-sided p-value is computed as 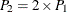 .
.
Noninferiority Tests
If you specify the NONINF riskdiff-option, PROC FREQ provides a noninferiority test for the risk difference, or the difference between two proportions. The null hypothesis for the noninferiority test is
![\[ H_0\colon p_1 - p_2 \leq -\delta \]](images/statug_freq0348.png)
versus the alternative
![\[ H_ a\colon p_1 - p_2 > -\delta \]](images/statug_freq0349.png)
where  is the noninferiority margin. Rejection of the null hypothesis indicates that the row 1 risk is not inferior to the row 2
risk. See Chow, Shao, and Wang (2003) for more information.
is the noninferiority margin. Rejection of the null hypothesis indicates that the row 1 risk is not inferior to the row 2
risk. See Chow, Shao, and Wang (2003) for more information.
You can specify the value of  with the MARGIN= riskdiff-option. By default,
with the MARGIN= riskdiff-option. By default, 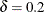 . You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference noninferiority analysis: Wald (with and without continuity correction),
Hauck-Anderson, Farrington-Manning (score), and Newcombe (with and without continuity correction). The Wald, Hauck-Anderson,
and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe method provides
only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
. You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference noninferiority analysis: Wald (with and without continuity correction),
Hauck-Anderson, Farrington-Manning (score), and Newcombe (with and without continuity correction). The Wald, Hauck-Anderson,
and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe method provides
only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
The confidence coefficient for the test-based confidence limits is 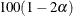 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 90% confidence limits. You can compare the confidence limits
to the noninferiority limit, –
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 90% confidence limits. You can compare the confidence limits
to the noninferiority limit, – .
.
The following sections describe the noninferiority analysis methods for the risk difference.
Wald Test
If you specify the METHOD=WALD riskdiff-option, PROC FREQ provides an asymptotic Wald test of noninferiority for the risk difference. This is also the default method. The
Wald test statistic is computed as
![\[ z = ( \hat{d} + \delta ) ~ / ~ \mr{se}(\hat{d}) \]](images/statug_freq0350.png)
where (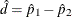 ) estimates the risk difference and
) estimates the risk difference and  is the noninferiority margin.
is the noninferiority margin.
By default, the standard error for the Wald test is computed from the sample proportions as
![\[ \mr{se}(\hat{d}) = \sqrt { \hat{p}_1 (1 - \hat{p}_1) / n_{1 \cdot } ~ +~ \hat{p}_2 (1 - \hat{p}_2) / n_{2 \cdot } } \]](images/statug_freq0351.png)
If you specify the VAR=NULL riskdiff-option, the standard error is based on the null hypothesis that the risk difference equals – (Dunnett and Gent 1977). The standard error is computed as
(Dunnett and Gent 1977). The standard error is computed as
![\[ \mr{se}(\hat{d}) = \sqrt { \tilde{p} (1-\tilde{p})/n_{2 \cdot } ~ +~ (\tilde{p} - \delta ) (1-\tilde{p} + \delta ) / n_{1 \cdot } } \]](images/statug_freq0352.png)
where
![\[ \tilde{p} = ( n_{11} + n_{21} + \delta n_{1 \cdot } ) / n \]](images/statug_freq0353.png)
If you specify the CORRECT riskdiff-option, the test statistic includes a continuity correction. The continuity correction is subtracted from the numerator of the test
statistic if the numerator is greater than 0; otherwise, the continuity correction is added to the numerator. The value of
the continuity correction is 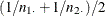 .
.
The p-value for the Wald noninferiority test is 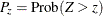 , where Z has a standard normal distribution.
, where Z has a standard normal distribution.
Hauck-Anderson Test
If you specify the METHOD=HA riskdiff-option, PROC FREQ provides the Hauck-Anderson test for noninferiority. The Hauck-Anderson test statistic is computed as
![\[ z = ( \hat{d} + \delta ~ \pm ~ \mathit{cc}) ~ / ~ \mr{se}(\hat{d}) \]](images/statug_freq0356.png)
where 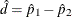 and the standard error is computed from the sample proportions as
and the standard error is computed from the sample proportions as
![\[ \mr{se}(\hat{d}) = \sqrt { \hat{p}_1 (1-\hat{p}_1) / (n_{1 \cdot }-1) ~ +~ \hat{p}_2 (1-\hat{p}_2) / (n_{2 \cdot }-1) } \]](images/statug_freq0302.png)
The Hauck-Anderson continuity correction cc is computed as
![\[ \mathit{cc} = 1 ~ / ~ \bigl ( 2 ~ \min ( n_{1 \cdot }, ~ n_{2 \cdot } ) \bigr ) \]](images/statug_freq0303.png)
The p-value for the Hauck-Anderson noninferiority test is 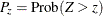 , where Z has a standard normal distribution. See Hauck and Anderson (1986) and Schuirmann (1999) for more information.
, where Z has a standard normal distribution. See Hauck and Anderson (1986) and Schuirmann (1999) for more information.
Farrington-Manning (Score) Test
If you specify the METHOD=FM riskdiff-option, PROC FREQ provides the Farrington-Manning (score) test of noninferiority for the risk difference. A score test statistic
for the null hypothesis that the risk difference equals – can be expressed as
can be expressed as
![\[ z = ( \hat{d} + \delta ) ~ / ~ \mr{se}(\hat{d}) \]](images/statug_freq0350.png)
where 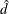 is the observed value of the risk difference (
is the observed value of the risk difference (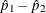 ),
),
![\[ \mr{se}(\hat{d}) = \sqrt { \tilde{p}_1 (1-\tilde{p}_1) / n_{1 \cdot } ~ +~ \tilde{p}_2 (1-\tilde{p}_2) / n_{2 \cdot } } \]](images/statug_freq0357.png)
and 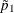 and
and 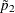 are the maximum likelihood estimates of the row 1 and row 2 risks (proportions) under the restriction that the risk difference
is –
are the maximum likelihood estimates of the row 1 and row 2 risks (proportions) under the restriction that the risk difference
is – . The p-value for the noninferiority test is
. The p-value for the noninferiority test is 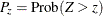 , where Z has a standard normal distribution. For more information, see Miettinen and Nurminen (1985); Miettinen (1985); Farrington and Manning (1990); Dann and Koch (2005).
, where Z has a standard normal distribution. For more information, see Miettinen and Nurminen (1985); Miettinen (1985); Farrington and Manning (1990); Dann and Koch (2005).
The maximum likelihood estimates of 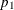 and
and 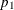 , subject to the constraint that the risk difference is –
, subject to the constraint that the risk difference is – , are computed as
, are computed as
![\[ \tilde{p}_1 = 2 u \cos (w) - b/3a \hspace{.15in} \mr{and} \hspace{.15in} \tilde{p}_2 = \tilde{p}_1 + \delta \]](images/statug_freq0316b.png)
where
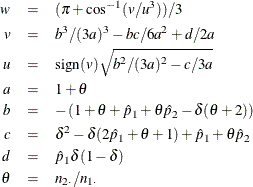
For more information, see Farrington and Manning (1990, p. 1453).
Newcombe Noninferiority Analysis
If you specify the METHOD=NEWCOMBE riskdiff-option, PROC FREQ provides a noninferiority analysis that is based on Newcombe hybrid-score confidence limits for the risk difference.
The confidence coefficient for the confidence limits is 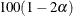 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 90% confidence limits. You can compare the confidence limits
with the noninferiority limit, –
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 90% confidence limits. You can compare the confidence limits
with the noninferiority limit, – . If you specify the CORRECT riskdiff-option, the confidence limits includes a continuity correction. See the subsection "Newcombe Confidence Limits" in the section Confidence Limits for the Risk Difference for more information.
. If you specify the CORRECT riskdiff-option, the confidence limits includes a continuity correction. See the subsection "Newcombe Confidence Limits" in the section Confidence Limits for the Risk Difference for more information.
Superiority Test
If you specify the SUP riskdiff-option, PROC FREQ provides a superiority test for the risk difference. The null hypothesis is
![\[ H_0\colon : p_1 - p_2 \leq \delta \]](images/statug_freq0361.png)
versus the alternative
![\[ H_ a\colon p_1 - p_2 > \delta \]](images/statug_freq0362.png)
where  is the superiority margin. Rejection of the null hypothesis indicates that the row 1 proportion is superior to the row 2
proportion. You can specify the value of
is the superiority margin. Rejection of the null hypothesis indicates that the row 1 proportion is superior to the row 2
proportion. You can specify the value of  with the MARGIN= riskdiff-option. By default,
with the MARGIN= riskdiff-option. By default, 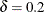 .
.
The superiority analysis is identical to the noninferiority analysis but uses a positive value of the margin  in the null hypothesis. The superiority computations follow those in the section Noninferiority Tests by replacing –
in the null hypothesis. The superiority computations follow those in the section Noninferiority Tests by replacing – by
by  . See Chow, Shao, and Wang (2003) for more information.
. See Chow, Shao, and Wang (2003) for more information.
Equivalence Test
If you specify the EQUIV riskdiff-option, PROC FREQ provides an equivalence test for the risk difference, or the difference between two proportions. The null hypothesis for the equivalence test is
![\[ H_0\colon p_1 - p_2 \leq -\delta _{\mi{L}} \hspace{.15in} \mr{or} \hspace{.15in} p_1 - p_2 \geq \delta _{\mi{U}} \]](images/statug_freq0363.png)
versus the alternative
![\[ H_ a\colon \delta _{\mi{L}} < p_1 - p_2 < \delta _{\mi{U}} \]](images/statug_freq0364.png)
where 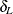 is the lower margin and
is the lower margin and 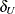 is the upper margin. Rejection of the null hypothesis indicates that the two binomial proportions are equivalent. See Chow,
Shao, and Wang (2003) for more information.
is the upper margin. Rejection of the null hypothesis indicates that the two binomial proportions are equivalent. See Chow,
Shao, and Wang (2003) for more information.
You can specify the value of the margins 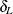 and
and 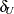 with the MARGIN= riskdiff-option. If you do not specify MARGIN=, PROC FREQ uses lower and upper margins of –0.2 and 0.2 by default. If you specify a single
margin value
with the MARGIN= riskdiff-option. If you do not specify MARGIN=, PROC FREQ uses lower and upper margins of –0.2 and 0.2 by default. If you specify a single
margin value  , PROC FREQ uses lower and upper margins of –
, PROC FREQ uses lower and upper margins of – and
and  . You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference equivalence analysis: Wald (with and without continuity correction),
Hauck-Anderson, Farrington-Manning (score), and Newcombe (with and without continuity correction). The Wald, Hauck-Anderson,
and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe method provides
only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
. You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference equivalence analysis: Wald (with and without continuity correction),
Hauck-Anderson, Farrington-Manning (score), and Newcombe (with and without continuity correction). The Wald, Hauck-Anderson,
and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe method provides
only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
PROC FREQ computes two one-sided tests (TOST) for equivalence analysis
(Schuirmann 1987). The TOST approach includes a right-sided test for the lower margin 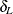 and a left-sided test for the upper margin
and a left-sided test for the upper margin 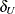 . The overall p-value is taken to be the larger of the two p-values from the lower and upper tests.
. The overall p-value is taken to be the larger of the two p-values from the lower and upper tests.
The section Noninferiority Tests gives details about the Wald, Hauck-Anderson, Farrington-Manning (score), and Newcombe methods for the risk difference. The
lower margin equivalence test statistic takes the same form as the noninferiority test statistic but uses the lower margin
value 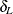 in place of –
in place of – . The upper margin equivalence test statistic take the same form as the noninferiority test statistic but uses the upper margin
value
. The upper margin equivalence test statistic take the same form as the noninferiority test statistic but uses the upper margin
value 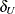 in place of –
in place of – .
.
The test-based confidence limits for the risk difference are computed according to the equivalence test method that you select.
If you specify METHOD=WALD with VAR=NULL, or METHOD=FM, separate standard errors are computed for the lower and upper margin
tests. In this case, the test-based confidence limits are computed by using the maximum of these two standard errors. These
confidence limits have a confidence coefficient of 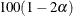 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 90% confidence limits. You can compare the test-based confidence
limits to the equivalence limits,
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 90% confidence limits. You can compare the test-based confidence
limits to the equivalence limits, 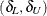 .
.
Barnard’s Unconditional Exact Test
The BARNARD option in the EXACT statement provides an unconditional exact test for the risk (proportion) difference for 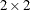 tables. The reference set for the unconditional exact test consists of all
tables. The reference set for the unconditional exact test consists of all 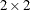 tables that have the same row sums as the observed table (Barnard 1945, 1947, 1949). This differs from the reference set for exact conditional inference, which is restricted to the set of tables that have
the same row sums and the same column sums as the observed table. See the sections Fisher’s Exact Test and Exact Statistics for more information.
tables that have the same row sums as the observed table (Barnard 1945, 1947, 1949). This differs from the reference set for exact conditional inference, which is restricted to the set of tables that have
the same row sums and the same column sums as the observed table. See the sections Fisher’s Exact Test and Exact Statistics for more information.
The test statistic is the standardized risk difference, which is computed as
![\[ T = d / \sqrt { p_{\cdot 1} ( 1 - p_{\cdot 1} ) ( 1/n_1 + 1/n_2 ) } \]](images/statug_freq0366.png)
where the risk difference d is defined as the difference between the row 1 and row 2 risks (proportions), 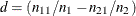 ;
; 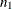 and
and 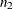 are the row 1 and row 2 totals, respectively; and
are the row 1 and row 2 totals, respectively; and 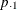 is the overall proportion in column 1,
is the overall proportion in column 1, 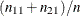 .
.
Under the null hypothesis that the risk difference is 0, the joint probability function for a table can be expressed in terms
of the table cell frequencies, the row totals, and the unknown parameter  as
as
![\[ f( n_{11}, n_{21}; n_1, n_2, \pi ) = \binom {n_1}{n_{11}} \binom {n_2}{n_{21}} \pi ^{n_{11} + n_{21}} (1-\pi )^{n - n_{11} - n_{21}} \]](images/statug_freq0371.png)
where  is the common value of the risk (proportion).
is the common value of the risk (proportion).
PROC FREQ sums the table probabilities over the reference set for those tables where the test statistic is greater than or equal to the observed value of the test statistic. This sum can be expressed as
![\[ \mr{Prob}( \pi ) = \sum _{A, T(a) \geq t_0} f( n_{11}, n_{21}; n_1, n_2, \pi ) \]](images/statug_freq0372.png)
where the set A contains all 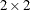 tables with row sums equal to
tables with row sums equal to 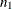 and
and 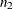 , and
, and 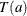 denotes the value of the test statistic for table a in A. The sum includes probabilities of those tables for which (
denotes the value of the test statistic for table a in A. The sum includes probabilities of those tables for which (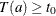 ), where
), where 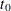 is the value of the test statistic for the observed table.
is the value of the test statistic for the observed table.
The sum Prob( ) depends on the unknown value of
) depends on the unknown value of  . To compute the exact p-value, PROC FREQ eliminates the nuisance parameter
. To compute the exact p-value, PROC FREQ eliminates the nuisance parameter  by taking the maximum value of Prob(
by taking the maximum value of Prob( ) over all possible values of
) over all possible values of  ,
,
![\[ \mr{Prob} = \sup _{ ( 0 \leq \pi \leq 1 ) } { \left( \mr{Prob}( \pi ) \right) } \]](images/statug_freq0373.png)
See Suissa and Shuster (1985) and Mehta and Senchaudhuri (2003).