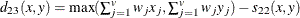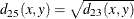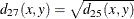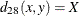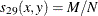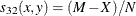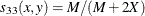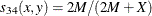The DISTANCE Procedure
Proximity Measures
The following notation is used in this section:
- v
-
the number of variables or the dimensionality
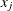
-
data for observation x and the jth variable, where
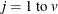
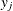
-
data for observation y and the jth variable, where
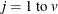
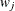
-
weight for the jth variable from the WEIGHTS= option in the VAR statement.
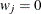 when either
when either 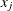 or
or 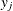 is missing.
is missing.
- W
-
the sum of total weights. No matter if the observation is missing or not, its weight is added to this metric.

-
mean for observation x
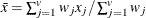
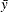
-
mean for observation y
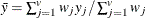
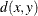
-
the distance or dissimilarity between observations x and y
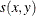
-
the similarity between observations x and y
The factor 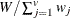 is used to adjust some of the proximity measures for missing values.
is used to adjust some of the proximity measures for missing values.
Methods That Accept All Measurement Levels
Methods That Accept Ratio, Interval, and Ordinal Variables
- EUCLID
- SQEUCLID
- SIZE
- SHAPE
-
Note: squared shape distance plus squared size distance equals squared Euclidean distance.
- COV
-
covariance similarity coefficient
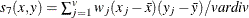 , where
, where
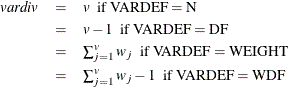
- CORR
- DCORR
-
correlation transformed to Euclidean distance as sqrt(1–CORR)
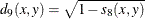
- SQCORR
- DSQCORR
-
squared correlation transformed to squared Euclidean distance as (1–SQCORR)
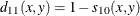
- L(p)
-
Minkowski (
 ) distance, where p is a positive numeric value
) distance, where p is a positive numeric value
![$ d_{12}(x,y) = [ (\sum _{j=1}^ v{w_ j{|x_ j-y_ j|}^ p}) W / (\sum _{j=1}^{v}w_ j) ]^{1/p} $](images/statug_distance0064.png)
- CITYBLOCK
- CHEBYCHEV
- POWER(p,r)
-
generalized Euclidean distance, where p is a nonnegative numeric value and r is a positive numeric value. The distance between two observations is the rth root of sum of the absolute differences to the pth power between the values for the observations:
![$ d_{15}(x,y) = [ (\sum _{j=1}^ v{w_ j{|x_ j-y_ j| }^ p}) W / (\sum _{j=1}^{v}w_ j) ]^{1/r} $](images/statug_distance0067.png)
Methods That Accept Ratio Variables
- SIMRATIO
- DISRATIO
- NONMETRIC
- CANBERRA
-
Canberra metric coefficient. See Sneath and Sokal (1973, pp. 125–126)
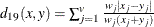
- COSINE
- DOT
- OVERLAP
- DOVERLAP
- CHISQ
-
chi-square If the data represent the frequency counts, chi-square dissimilarity between two sets of frequencies can be computed. A 2-by-v contingency table is illustrated to explain how the chi-square dissimilarity is computed as follows:
Variable
Row
Observation
Var 1
Var 2
…
Var v
Sum
X
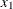
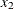
…
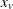
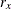
Y
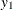
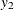
…
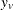
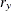
Column Sum
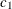
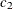
…
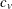
T
where
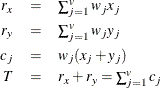
The chi-square measure is computed as follows:
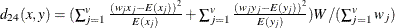
where for j= 1, 2, …, v
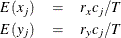
- CHI
- PHISQ
-
phi-square This is the CHISQ dissimilarity normalized by the sum of weights
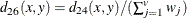
- PHI
Methods That Accept Symmetric Nominal Variables
The following notation is used for computing 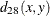 to
to 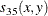 . Notice that only the nonmissing pairs are discussed below; all the pairs with at least one missing value will be excluded
from any of the computations in the following section because
. Notice that only the nonmissing pairs are discussed below; all the pairs with at least one missing value will be excluded
from any of the computations in the following section because 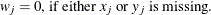
- M
-
nonmissing matches
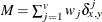 , where
, where
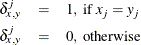
- X
-
nonmissing mismatches
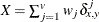 , where
, where
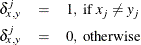
- N
-
total nonmissing pairs
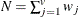
- HAMMING
- MATCH
- DMATCH
-
simple matching coefficient transformed to Euclidean distance
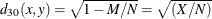
- DSQMATCH
-
simple matching coefficient transformed to squared Euclidean distance
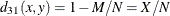
- HAMANN
- RT
- SS1
- SS3
-
Sokal and Sneath 3. The coefficient between an observation and itself is always indeterminate (missing) since there is no mismatch.
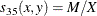
The following notation is used for computing 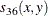 to
to 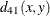 . Notice that only the nonmissing pairs are discussed in the following section; all the pairs with at least one missing value
are excluded from any of the computations in the following section because
. Notice that only the nonmissing pairs are discussed in the following section; all the pairs with at least one missing value
are excluded from any of the computations in the following section because 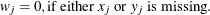
Also, the observed nonmissing data of an asymmetric binary variable can have only two possible outcomes: presence or absence. Therefore, the notation, PX (present mismatches), always has a value of zero for an asymmetric binary variable.
The following methods distinguish between the presence and absence of attributes.
- X
-
mismatches with at least one present
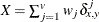 , where
, where

- PM
-
present matches
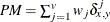 , where
, where
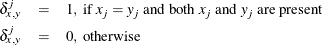
- PX
-
present mismatches
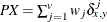 , where
, where
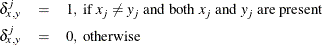
- PP
-
both present = PM + PX
- P
-
at least one present = PM + X
- PAX
-
present-absent mismatches
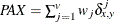 , where
, where
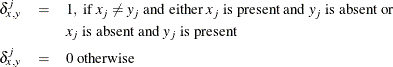
- N
-
total nonmissing pairs
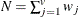
Methods That Accept Asymmetric Nominal and Ratio Variables
- JACCARD
-
Jaccard similarity coefficient
The JACCARD method is equivalent to the SIMRATIO method if there are only ratio variables; if there are both ratio and asymmetric nominal variables, the coefficient is computed as sum of the coefficient from the ratio variables (SIMRATIO) and the coefficient from the asymmetric nominal variables.
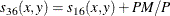
- DJACCARD
-
Jaccard dissimilarity coefficient
The DJACCARD method is equivalent to the DISRATIO method if there are only ratio variables; if there are both ratio and asymmetric nominal variables, the coefficient is computed as sum of the coefficient from the ratio variables (DISRATIO) and the coefficient from the asymmetric nominal variables.
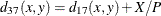
Methods That Accept Asymmetric Nominal Variables
- DICE
-
Dice coefficient or Czekanowski/Sorensen similarity coefficient
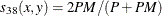
- RR
-
Russell and Rao. This is the binary equivalent of the dot product coefficient.
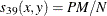
- BLWNM | BRAYCURTIS
-
Binary Lance and Williams, also known as Bray and Curtis coefficient
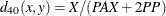
- K1
-
Kulcynski 1. The coefficient between an observation and itself is always indeterminate (missing) since there is no mismatch.
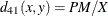

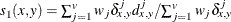
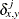
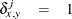
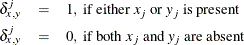
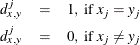
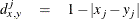
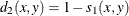
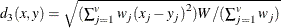
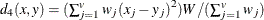
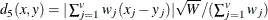
![$ d_{6}(x,y) = \sqrt { (\sum _{j=1}^{v}w_ j[(x_ j-\bar{x})- (y_ j-\bar{y})]^2) W / (\sum _{j=1}^{v}w_ j) }$](images/statug_distance0057.png)
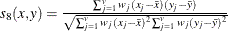
![$ s_{10}(x,y) = \frac{[\sum _{j=1}^{v}w_ j(x_ j-\bar{x}) (y_ j-\bar{y})]^2}{\sum _{j=1}^{v}w_ j(x_ j-\bar{x})^2 \sum _{j=1}^{v}w_ j(y_ j-\bar{y})^2} $](images/statug_distance0062.png)
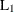
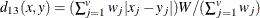
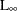
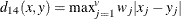
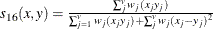
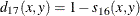
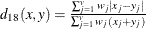
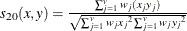
![$ s_{21}(x,y) = [\sum _{j=1}^{v}w_ j(x_{j}y_ j)]/ \sum _{j=1}^{v}w_ j $](images/statug_distance0073.png)
![$ s_{22}(x,y) = \sum _{j=1}^{v}w_ j[\min (x_ j,y_ j)]$](images/statug_distance0074.png)