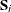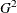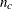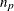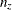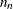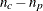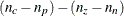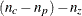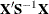The CATMOD Procedure

MODEL Statement

Subsections:

Specifying the Design Matrix Directly

MODEL response-effect = <design-effects> </ options>;

PROC CATMOD requires a MODEL statement. You can specify the following in a MODEL statement:

response-effect

can be either a single variable, a crossed effect with two or more variables joined by asterisks, or _F_. The _F_ specification indicates that the response functions and their estimated covariance matrix are to be read directly into the procedure (see the section Inputting Response Functions and Covariances Directly for details). The response-effect indicates the dependent variables that determine the response categories (the columns of the underlying contingency table).

design-effects

specify potential sources of variation (such as main effects and interactions) in the model. These effects determine the number of model parameters, as well as the interpretation of such parameters. In addition, if there is no POPULATION statement, PROC CATMOD uses these variables to determine the populations (the rows of the underlying contingency table). When fitting the model, PROC CATMOD adjusts the independent effects in the model for all other independent effects in the model.

Design-effects can be any of those described in the section Specification of Effects, or they can be defined by specifying the actual design matrix, enclosed in parentheses (see the section Specifying the Design Matrix Directly). In addition, you can use the keyword _RESPONSE_ alone or as part of an effect. Effects cannot be nested within _RESPONSE_, so effects of the form A(_RESPONSE_) are invalid.

For more information, see the section Log-Linear Model Analysis and the section Repeated Measures Analysis.

Some example MODEL statements are shown in the following table:

Example	Result
`model r=a b;`	Main effects only
`model r=a b a*b;`	Main effects with interaction
`model r=a b(a);`	Nested effect
`model r=a\|b;`	Complete factorial
`model r=a b(a=1) b(a=2);`	Nested-by-value effects
`model r*s=_response_;`	Log-linear model
`model r*s=a _response_(a);`	Nested repeated measurement factor
`model _f_=_response_;`	Direct input of the response functions

The relationship between these specifications and the structure of the design matrix 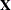$\mb{X}$ is described in the section Generation of the Design Matrix.

Table 32.5 summarizes the options available in the MODEL statement.

Table 32.5: MODEL Statement Options

Options	Task
Specify details of computation
ML=	Generates the maximum likelihood estimates
GLS	Generates the weighted least squares estimates
WLS
NOINT	Omits the intercept term from the model
PARAM=	Specifies the parameterization of classification variables
ADDCELL=	Adds a number to each cell frequency
AVERAGED	Averages the main effects across response functions
EPSILON=	Specifies the convergence criterion for maximum likelihood
MAXITER=	Specifies the number of iterations for maximum likelihood
MISSING=	Specifies how missing cells are treated
ZERO=	Specifies how zero cells are treated
Request additional computation and tables
ALPHA=	Specifies the significance level of confidence intervals
CLPARM	Displays the Wald confidence intervals of estimates
CORRB	Displays the estimated correlation matrix of estimates
COV	Displays the covariance matrix of response functions
COVB	Displays the estimated covariance matrix of estimates
DESIGN	Displays the design and _RESPONSE_ matrix
FREQ	Displays the two-way frequency tables
ITPRINT	Displays the iterations for maximum likelihood
ONEWAY	Displays the one-way frequency tables
PRED=	Displays the predicted values
PREDICT
PROB	Displays the probability estimates
PROFILE	Displays the population profiles
XPX	Displays the crossproducts matrix
TITLE=	Specifies the title
Suppress output
NODESIGN	Suppresses the design matrix
NOPARM	Suppresses the parameter estimates
NOPREDVAR	Suppresses the variable levels
NOPROFILE	Suppresses the population and response profiles
NORESPONSE	Suppresses the _RESPONSE_ matrix

The following list describes these options in alphabetical order.

ADDCELL=number

adds number to the frequency count in each cell, where number is any positive number. This option has no effect on maximum likelihood analysis; it is used only for weighted least squares analysis.

ALPHA=number

sets the significance level for the Wald confidence intervals for parameter estimates. The value must be between 0 and 1. The default value of 0.05 results in the calculation of a 95% confidence interval. This option has no effect unless the CLPARM option is also specified.

AVERAGED

specifies that dependent variable effects can be modeled and that independent variable main effects are averaged across the response functions in a population. For further information about the effect of using (or not using) the AVERAGED option, see the section Generation of the Design Matrix. Direct input of the design matrix or specification of the _RESPONSE_ keyword in the MODEL statement automatically uses an AVERAGED model type.

CLPARM

produces Wald confidence limits for the parameter estimates. The confidence coefficient can be specified with the ALPHA= option.

CORRB

displays the estimated correlation matrix of the parameter estimates.

COV

displays $\mb{S}_ i$ , which is the covariance matrix of the response functions for each population.

COVB

displays the estimated covariance matrix of the parameter estimates.

DESIGN

displays the design matrix $\mb{X}$ for WLS and ML analyses, and also displays the _RESPONSE_ matrix for log-linear models. For further information, see the section Generation of the Design Matrix.

EPSILON=number

specifies the convergence criterion for the maximum likelihood estimation of the parameters. The iterative estimation process stops when the proportional change in the log likelihood is less than number, or after the number of iterations specified by the MAXITER= option, whichever comes first. By default, EPSILON=1E–8.

FREQ

produces the two-way frequency table for the cross-classification of populations by responses.

ITPRINT

displays parameter estimates and other information at each iteration of a maximum likelihood analysis.

MAXITER=number

specifies the maximum number of iterations used for the maximum likelihood estimation of the parameters. By default, MAXITER=20.

ML <= NR | IPF<( ipf-options )> >

computes maximum likelihood estimates (MLE) by using either a Newton-Raphson algorithm (NR) or an iterative proportional fitting algorithm (IPF).

The option ML=NR (or simply ML) is available when you use generalized logits, and also when you perform binary logistic regression with logits, cumulative logits, or adjacent category logits. For generalized logits (the default response functions), ML=NR is the default estimation method.

The option ML=IPF is available for fitting a hierarchical log-linear model with one population (no independent variables and no population variables). The use of bar notation to express the log-linear effects guarantees that the model is hierarchical (the presence of any interaction term in the model requires the presence of all its lower-order terms). If your table is incomplete (that is, your table has a zero or missing entry in at least one cell), then all missing cells and all cells with zero weight are treated as structural zeros by default; this behavior can be modified with the ZERO= and MISSING= options in the MODEL statement.

You can control the convergence of the two algorithms with the EPSILON= and MAXITER= options in the MODEL statement. You can select the convergence criterion for the IPF algorithm with the CONVCRIT= option.

Note: The RESTRICT statement is not available with the ML=IPF option.

You can specify the following ipf-options within parentheses after the ML=IPF option.

CONVCRIT=keyword

specifies the method that determines when convergence of the IPF algorithm occurs. You can specify one of the following keywords:

CELL: termination requires the maximum absolute difference between consecutive cell estimates to be less than 0.001 (or the value of the EPSILON= option, if specified).
LOGL: termination requires the relative difference between consecutive estimates of the log likelihood to be less than 1E–8 (or the value of the EPSILON= option, if specified). This is the default.
MARGIN: termination requires the maximum absolute difference between consecutive margin estimates to be less than 0.001 (or the value of the EPSILON= option, if specified).

DF=keyword

specifies the method used to compute the degrees of freedom for the goodness-of-fit $G^2$ test (labeled "Likelihood Ratio" in the "Estimates" table).

For a complete table (a table having nonzero entries in every cell), the degrees of freedom are calculated as the number of cells in the table ( $n_ c$ ) minus the number of independent parameters specified in the model ( $n_ p$ ). For incomplete tables, these degrees of freedom can be adjusted by the number of fitted zeros ( $n_ z$ , which includes the number of structural zeros) and the number of nonestimable parameters due to the zeros ( $n_ n$ ). If you are analyzing an incomplete table, you should verify that the degrees of freedom are correct.

You can specify one of the following keywords:

UNADJ: computes the unadjusted degrees of freedom as $n_ c-n_ p$ . These are the same degrees of freedom you would get if all cells in the table were positive.
ADJ: computes the degrees of freedom as $(n_ c-n_ p)-(n_ z-n_ n)$ (Bishop, Fienberg, and Holland 1975), which adjusts for fitted zeros and nonestimable parameters. This is the default, and for complete tables it gives the same results as the UNADJ option.
ADJEST: computes the degrees of freedom as $(n_ c-n_ p)-n_ z$ , which adjusts for fitted zeros only. This gives a lower bound on the true degrees of freedom.

PARM

computes parameter estimates, generates the "ANOVA," "Parameter Estimates," and "Predicted Values of Response Functions" tables, and includes the predicted standard errors in the "Predicted Values of Frequencies and Probabilities" tables.

When you specify the PARM option, the algorithm used to obtain the maximum likelihood parameter estimates is weighted least squares on the IPF-predicted frequencies. This algorithm can be much faster than the Newton-Raphson algorithm that is used if you specify the ML=NR option. In the resulting ANOVA table, the likelihood ratio is computed from the initial IPF fit while the degrees of freedom are generated from the WLS analysis; the DF= option can override this. Also, the initial response function, which the WLS method usually computes from the raw data, is computed from the IPF-predicted frequencies.

If there are any zero marginals in the configurations that define the model, then there are predicted cell frequencies of zero and WLS cannot be used to compute the estimates. In this case, PROC CATMOD automatically changes the algorithm from ML=IPF to ML=NR and prints a note in the log.

MISSING=keyword MISS=keyword

specifies whether a missing cell is treated as a sampling or structural zero.

Structural zero cells are removed from the analysis since their expected values are zero, while sampling zero cells can have nonzero expected value and might be estimable. For a single population, the missing cells are treated as structural zeros by default. For multiple populations, as long as some population has a nonzero count for a given population and response profile, the missing values are treated as sampling zeros by default.

The following table displays the available keywords and summarizes how PROC CATMOD treats missing values for one or more populations:

MISSING=	One Population	Multiple Populations
STRUCTURAL (default)	Structural zeros	Sampling zeros
SAMP \| SAMPLING	Sampling zeros	Sampling zeros
value	Sets missing weights and cells to value	Sets missing weights and cells to value

NODESIGN

suppresses the display of the design matrix $\mb{X}$ when the DESIGN option is also specified. This enables you to display only the _RESPONSE_ matrix for log-linear models.

NOINT

suppresses the intercept term in the model.

NOPARM

suppresses the display of the estimated parameters and the statistics for testing that each parameter is zero.

NOPREDVAR

suppresses the display of the variable levels in tables requested with the PRED= option and in the "Estimates" table. Population profiles are replaced with the sample number, classification variable levels are suppressed, and response profiles are replaced with a function number.

NOPRINT

suppresses the normal display of results. The NOPRINT option is useful when you only want to create output data sets with the OUT= or OUTEST= option in the RESPONSE statement. A NOPRINT option is also available in the PROC CATMOD statement. Note that this option temporarily disables the Output Delivery System (ODS); see Chapter 20: Using the Output Delivery System, for more information.

NOPROFILE

suppresses the display of the population profiles and the response profiles.

NORESPONSE

suppresses the display of the _RESPONSE_ matrix for log-linear models when the DESIGN option is also specified. This enables you to display only the design matrix for log-linear models.

ONEWAY

produces a one-way table of frequencies for each variable used in the analysis. This table is useful in determining the order of the observed levels for each variable.

PARAM=EFFECT | REFERENCE

specifies the parameterization method for the classification variable or variables. The default is PARAM=EFFECT. Both the effect and reference parameterizations are full rank. See the section Generation of the Design Matrix for further details.

PREDICT PRED=FREQ | PROB

displays the observed and predicted values of the response functions for each population, together with their standard errors and the residuals (observed minus predicted). In addition, if the response functions are the standard ones (generalized logits), then the PRED=FREQ option specifies the computation and display of predicted cell frequencies, while PRED=PROB (or just PREDICT) specifies the computation and display of predicted cell probabilities.

The OUT= data set always contains the predicted probabilities. If the response functions are the generalized logits, the predicted cell probabilities are output unless the option PRED=FREQ is specified, in which case the predicted cell frequencies are output.

PROB

produces the two-way table of probability estimates for the cross-classification of populations by responses. These estimates sum to one across the response categories for each population.

PROFILE

displays all of the population profiles. If you have more than 60 populations, then by default only the first 40 profiles are displayed; the PROFILE option overrides this default behavior.

TITLE=’title’

displays the title at the top of certain pages of output that correspond to this MODEL statement.

WLS GLS

computes weighted least squares estimates. This type of estimation is also called generalized least squares estimation. For response functions other than the default (of generalized logits), WLS is the default estimation method.

XPX

displays $\mb{X}’\mb{S}^{-1}\mb{X}$ , the crossproducts matrix for the normal equations.

ZERO=keyword

specifies whether a nonmissing cell with zero weight in the data set is treated as a sampling or structural zero.

Structural zero cells are removed from the analysis since their expected values are zero, while sampling zero cells have nonzero expected value and might be estimable. For a single population, the zero cells are treated as structural zeros by default; with multiple populations, as long as some population has a nonzero count for a given population and response profile, the zeros are treated as sampling zeros by default.

The following table displays the available keywords and summarizes how PROC CATMOD treats zeros for one or more populations:

ZERO=	One Population	Multiple Populations
STRUCTURAL (default)	Structural zeros	Sampling zeros
SAMP \| SAMPLING	Sampling zeros	Sampling zeros
value	Sets zero weights to value	Sets zero weights to value

Specifying the Design Matrix Directly

If you specify the design matrix directly, adjacent rows of the matrix must be separated by a comma, and the matrix must have 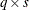$q \times s$ rows, where s is the number of populations and q is the number of response functions per population. The first q rows correspond to the response functions for the first population, the second set of q rows corresponds to the functions for the second population, and so forth. The following is an example of using direct specification of the design matrix.

proc catmod;
   model R=(1 0,
            1 1,
            1 2,
            1 3);
run;

These statements are appropriate for the case of one population and for R with five levels (generating four response functions), so that 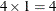$4 \times 1=4$ . These statements are also appropriate for a situation with two populations and two response functions per population, giving 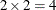$2 \times 2=4$ rows of the design matrix. (To accommodate more than one population, the POPULATION statement is needed.)

When you input the design matrix directly, you also have the option of specifying that any subsets of the parameters be tested for equality to zero. Indicate each subset by specifying the appropriate column numbers of the design matrix, followed by an equal sign and a label (24 characters or less, in quotes) that describes the subset. Adjacent subsets are separated by a comma, and the entire specification is enclosed in parentheses and placed after the design matrix. For example:

proc catmod;
   population Group Time;
   model R=(1  1  0  0,
            1  1  0  1,
            1  1  0  2,
            1  0  1  0,
            1  0  1  1,
            1  0  1  2,
            1 -1 -1  0,
            1 -1 -1  1,
            1 -1 -1  2) (1  ='Intercept',
                         2 3='Group main effect',
                         4  ='Linear effect of Time');
run;

The preceding statements are appropriate when Group and Time each have three levels and R is dichotomous. The POPULATION statement produces nine populations, and q = 1 (since R is dichotomous), so 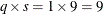$q \times s=1 \times 9=9$ .

If you input the design matrix directly but do not specify any subsets of the parameters to be tested, then PROC CATMOD tests the effect of MODEL | MEAN, which represents the significance of the model beyond what is explained by an overall mean. For the previous example, the MODEL | MEAN effect is the same as that obtained by specifying the following at the end of the MODEL statement:

(2 3 4='model|mean');