The SURVEYREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC SURVEYREG StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement
PROC SURVEYREG StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
Details

-
Examples

- References
This example illustrates the use of the SURVEYREG procedure to perform a regression in a stratified sample design. Consider
a population of 235 farms producing corn in Nebraska and Iowa. You are interested in the relationship between corn yield (CornYield) and total farm size (FarmArea).
Each state is divided into several regions, and each region is used as a stratum. Within each stratum, a simple random sample with replacement is drawn. A total of 19 farms is selected by using a stratified simple random sample. The sample size and population size within each stratum are displayed in Table 101.12.
Table 101.12: Number of Farms in Each Stratum
|
Number of Farms |
||||
|---|---|---|---|---|
|
Stratum |
State |
Region |
Population |
Sample |
|
1 |
Iowa |
1 |
100 |
3 |
|
2 |
2 |
50 |
5 |
|
|
3 |
3 |
15 |
3 |
|
|
4 |
Nebraska |
1 |
30 |
6 |
|
5 |
2 |
40 |
2 |
|
|
Total |
235 |
19 |
||
The following three models are considered:
-
Model I — Common intercept and slope:
![\[ \mbox{Corn Yield}=\alpha +\beta *\mbox{Farm Area} \]](images/statug_surveyreg0119.png)
-
Model II — Common intercept, different slope:
![\[ \mbox{Corn Yield} =\left\{ {\begin{array}{ll} \alpha +\beta _{\mbox{Iowa}}*\mbox{Farm Area} & \mbox{if the farm is in Iowa} \\ \alpha +\beta _{\mbox{Nebraska}}*\mbox{Farm Area} & \mbox{if the farm is in Nebraska} \end{array} } \right. \]](images/statug_surveyreg0120.png)
-
Model III — Different intercept and different slope:
![\[ \mbox{Corn Yield}=\left\{ {\begin{array}{ll} \alpha _{\mbox{Iowa}}+\beta _{\mbox{Iowa}}*\mbox{Farm Area} & \mbox{if the farm is in Iowa} \\ \alpha _{\mbox{Nebraska}}+\beta _{\mbox{Nebraska}}* \mbox{Farm Area} & \mbox{if the farm is in Nebraska} \end{array}} \right. \]](images/statug_surveyreg0121.png)
Data from the stratified sample are saved in the SAS data set Farms. The variable Weight contains the sampling weights, which are reciprocals of the selection probabilities.
data Farms; input State $ Region FarmArea CornYield Weight; datalines; Iowa 1 100 54 33.333 Iowa 1 83 25 33.333 Iowa 1 25 10 33.333 Iowa 2 120 83 10.000 Iowa 2 50 35 10.000 Iowa 2 110 65 10.000 Iowa 2 60 35 10.000 Iowa 2 45 20 10.000 Iowa 3 23 5 5.000 Iowa 3 10 8 5.000 Iowa 3 350 125 5.000 Nebraska 1 130 20 5.000 Nebraska 1 245 25 5.000 Nebraska 1 150 33 5.000 Nebraska 1 263 50 5.000 Nebraska 1 320 47 5.000 Nebraska 1 204 25 5.000 Nebraska 2 80 11 20.000 Nebraska 2 48 8 20.000 ;
The SAS data set StratumTotals contains the stratum population sizes.
data StratumTotals; input State $ Region _TOTAL_; datalines; Iowa 1 100 Iowa 2 50 Iowa 3 15 Nebraska 1 30 Nebraska 2 40 ;
Using the sample data from the data set Farms and the control information data from the data set StratumTotals, you can fit Model I by using the following statements in PROC SURVEYREG:
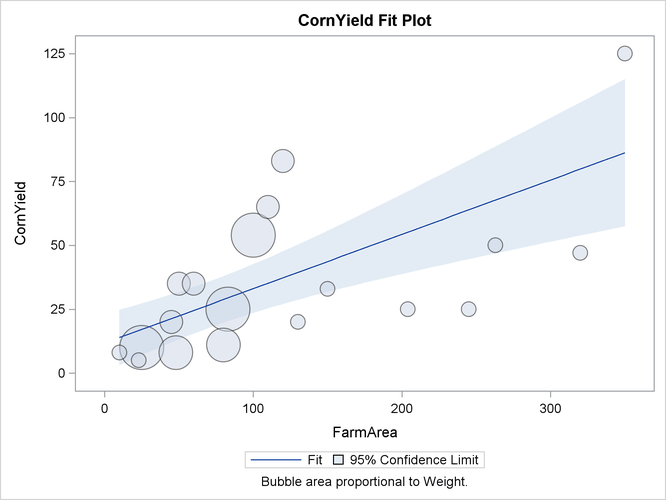
ods graphics on; title1 'Analysis of Farm Area and Corn Yield'; title2 'Model I: Same Intercept and Slope'; proc surveyreg data=Farms total=StratumTotals; strata State Region / list; model CornYield = FarmArea / covB; weight Weight; run; ods graphics off;
Output 101.4.1 displays the data summary and stratification information fitting Model I. The sampling rates are automatically computed by the procedure based on the sample sizes and the population totals in strata.
Output 101.4.2 displays tests of model effects and the estimated regression coefficients.
Output 101.4.3 displays the fit of the regression.
Alternatively, you can assume that the linear relationship between corn yield (CornYield) and farm area (FarmArea) is different among the states (Model II). In order to analyze the data by using this model, you create auxiliary variables
FarmAreaNE and FarmAreaIA to represent farm area in different states:
The following statements create these variables in a new data set called FarmsByState and use PROC SURVEYREG to fit Model II:
data FarmsByState;
set Farms;
if State='Iowa' then do;
FarmAreaIA=FarmArea;
FarmAreaNE=0;
end;
else do;
FarmAreaIA=0;
FarmAreaNE=FarmArea;
end;
run;
The following statements perform the regression by using the new data set FarmsByState. The analysis uses the auxiliary variables FarmAreaIA and FarmAreaNE as the regressors:
title1 'Analysis of Farm Area and Corn Yield'; title2 'Model II: Same Intercept, Different Slopes'; proc surveyreg data=FarmsByState total=StratumTotals; strata State Region; model CornYield = FarmAreaIA FarmAreaNE / covB; weight Weight; run;
Output 101.4.4 displays the fit statistics and parameter estimates. The estimated slope parameters for each state are quite different from the estimated slope in Model I. The results from the regression show that Model II fits these data better than Model I.
For Model III, different intercepts are used for the linear relationship in two states. The following statements illustrate the use of the NOINT option in the MODEL statement associated with the CLASS statement to fit Model III:
title1 'Analysis of Farm Area and Corn Yield'; title2 'Model III: Different Intercepts and Slopes'; proc surveyreg data=FarmsByState total=StratumTotals; strata State Region; class State; model CornYield = State FarmAreaIA FarmAreaNE / noint covB solution; weight Weight; run;
The model statement includes the classification effect State as a regressor. Therefore, the parameter estimates for effect State present the intercepts in two states.
Output 101.4.5 displays the regression results for fitting Model III, including parameter estimates, and covariance matrix of the regression coefficients. The estimated covariance matrix shows a lack of correlation between the regression coefficients from different states. This suggests that Model III might be the best choice for building a model for farm area and corn yield in these two states.
However, some statistics remain the same under different regression models—for example, Weighted Mean of CornYield. These estimators do not rely on the particular model you use.
Output 101.4.5: Regression Results for Fitting Model III
| Estimated Regression Coefficients | ||||
|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
t Value | Pr > |t| |
| State Iowa | 5.27797099 | 5.27170400 | 1.00 | 0.3337 |
| State Nebraska | 0.65275201 | 1.70031616 | 0.38 | 0.7068 |
| FarmAreaIA | 0.40680971 | 0.06458426 | 6.30 | <.0001 |
| FarmAreaNE | 0.14630563 | 0.01997085 | 7.33 | <.0001 |
| Note: | The degrees of freedom for the t tests is 14. |