The SURVEYPHREG Procedure

OUTPUT Statement

  • OUTPUT <OUT=SAS-data-set> <keyword=name …keyword=name> </ options>;

The OUTPUT statement creates a new SAS data set that contains statistics that are calculated for each observation unit. These statistics can include the estimated linear predictor (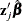$\mb{z}_{j}’{\hat{\bbeta }}$) and its standard error, residuals, and influence statistics. In addition, this data set includes all the variables from the DATA= input data set.

Only score residuals are available in the OUTPUT data set if the model contains a time-dependent variable that is defined by means of programming statements.

The following list explains specifications in the OUTPUT statement:

OUT=SAS-data-set

names the output data set. If you omit the OUT= option, the OUTPUT data set is named by using the DATAn convention. See the section OUT= Data Set for the OUTPUT statement for more information.

keyword=name

specifies the statistics to include in the OUTPUT data set and names the new variables that contain the statistics. Specify a keyword for each desired statistic (see the following list of keywords), and optionally an equal sign with either a variable or a list of variables in parentheses to contain the statistics. If you specify a keyword without a variable name, then the procedure uses default names. The keywords that accept a list of variables are RESSCH, RESSCO, and WTRESSCH. For these keywords, you can specify as many names in name as the number of explanatory variables in the MODEL statement. If you specify k names and k is less than the total number of explanatory variables, only the first k names are taken from the list; the procedure assigns default names for the rest of the statistics. The keywords and the corresponding statistics are as follows:

ATRISK

specifies the number of subjects at risk at the observation time 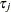$\tau _ j$.

RESDEV

specifies the deviance residual 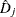${\hat{D}}_ j$. This is a transform of the martingale residual to achieve a more symmetric distribution.

RESMART

specifies the martingale residual 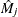${\hat{M}}_ j$. The residual at the observation time 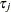$\tau _ j$ can be interpreted as the difference over $[0, {\tau }_{j}]$ in the observed number of events minus the expected number of events given by the model.

RESSCH

specifies the Schoenfeld residuals. These residuals are useful in assessing the proportional hazards assumption.

RESSCO

specifies the score residuals. These residuals are a decomposition of the first partial derivative of the log likelihood. They can be used to assess the leverage that is exerted by each subject in the parameter estimation. They are also useful in constructing design-based variance estimators.

STDXBETA

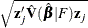specifies the standard error of the estimated linear predictor , $\sqrt { \mb{z}_{j}’\hat{\mb V} (\hat{\bbeta }|F) \mb{z}_{j} }$.

WTATRISK

specifies the weighted number of subjects at risk at the observation time 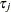$\tau _ j$.

XBETA

specifies the estimate of the linear predictor, 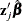$\mb{z}_{j}’\hat{\bbeta }$.