The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data - References
Measures of predictive accuracy of regression models quantify the extent to which covariates determine an individual outcome. Schemper and Henderson’s (2000) proposed predictive accuracy measure is defined as the difference between individual processes and the fitted survivor function.
For the ith individual (![]() ), let
), let ![]() and
and ![]() be the left-truncation time, observed time, event indicator (1 for death and 0 for censored), and covariate vector, respectively.
If there is no delay entry, then
be the left-truncation time, observed time, event indicator (1 for death and 0 for censored), and covariate vector, respectively.
If there is no delay entry, then ![]() . Let
. Let ![]() be m distinct event times with
be m distinct event times with ![]() deaths at
deaths at ![]() . The survival process
. The survival process ![]() for the ith individual is
for the ith individual is
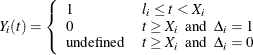
Let ![]() be the Kaplan-Meier estimate of the survivor function (assuming no covariates). Let
be the Kaplan-Meier estimate of the survivor function (assuming no covariates). Let ![]() be the fitted survivor function with covariates
be the fitted survivor function with covariates ![]() , and if you specify TIES=EFRON, then
, and if you specify TIES=EFRON, then ![]() is computed by the Efron method; otherwise, the Breslow estimate is used.
is computed by the Efron method; otherwise, the Breslow estimate is used.
The predictive accuracy is defined as the difference between individual survival processes ![]() and the fitted survivor functions with (
and the fitted survivor functions with (![]() )) or without (
)) or without (![]() ) covariates between 0 and
) covariates between 0 and ![]() , the largest observed time. For each death time
, the largest observed time. For each death time ![]() , define a mean absolute distance between the
, define a mean absolute distance between the ![]() and the
and the ![]() as
as
![\begin{eqnarray*} \hat{M}(t_{(j)}) & =& \frac{1}{n_ j} \sum _{i=1}^ n I(l_ i \le t_{(j)}) \biggl \{ I(X_ i>t_{(j)} \ge l_ i)(1-\hat{S}(t_{(j)}))+ \Delta _ i I(X_ i \leq t_{(j)})\hat{S}(t_{(j)}) \\ & & + ~ (1-\Delta _ i)I(X_ i \le t_{(j)}) \left[ (1-\hat{S}(t_{(j)}) )\frac{\hat{S}(t_{(j)})}{\hat{S}(X_ i)} +\hat{S}(t_{(j)}) \left(1 - \frac{\hat{S}(t_{(j)})}{\hat{S}(X_ i)} \right) \right] \biggr \} \end{eqnarray*}](images/statug_phreg0564.png)
where ![]() . Let
. Let ![]() be defined similarly to
be defined similarly to ![]() , but with
, but with ![]() replaced by
replaced by ![]() and
and ![]() replaced by
replaced by ![]() . Let
. Let ![]() be the Kaplan-Meier estimate of the censoring or potential follow-up distribution, and let
be the Kaplan-Meier estimate of the censoring or potential follow-up distribution, and let
The overall estimator of the predictive accuracy with (![]() ) and without (
) and without (![]() ) covariates are weighted averages of
) covariates are weighted averages of ![]() and
and ![]() , respectively, given by
, respectively, given by
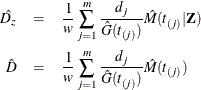
The explained variation by the Cox regression is
Because the predictive accuracy measures ![]() and
and ![]() are based on differences between individual survival processes and fitted survivor functions, a smaller value indicates a
better prediction. For this reason,
are based on differences between individual survival processes and fitted survivor functions, a smaller value indicates a
better prediction. For this reason, ![]() and
and ![]() are also referred to as predictive inaccuracy measures.
are also referred to as predictive inaccuracy measures.