The MDS Procedure

Formulas

The following notation is used:

$A_{p}$

intercept for partition p

$B_{p}$

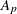
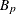
slope for partition p

$C_{p}$

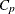
power for partition p

$D_{rcs}$

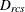
distance computed from the model between objects r and c for subject s

$F_{rcs}$

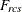
data weight for objects r and c for subject s obtained from the cth WEIGHT variable, or 1 if there is no WEIGHT statement

f

value of the FIT= option

N

number of objects

$O_{rcs}$

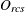
observed dissimilarity between objects r and c for subject s

$P_{rcs}$

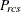
partition index for objects r and c for subject s

$Q_{rcs}$

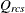
dissimilarity after applying any applicable estimated transformation for objects r and c for subject s

$R_{rcs}$

residual for objects r and c for subject s

$S_{p}$

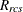
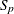
standardization factor for partition p

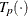
$T_{p}({\cdot })$

estimated transformation for partition p

$V_{sd}$

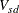
coefficient for subject s on dimension d

$X_{nd}$

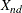
coordinate for object n on dimension d

Summations are taken over nonmissing values.

Distances are computed from the model as

\[ D_{rcs} = \begin{cases} \sqrt {\sum _ d(X_{rd}-X_{cd})^2} & \mbox{for COEF=IDENTITY:}\\ & \text {Euclidean distance}\\[2ex] \sqrt {\sum _ d V_{sd}^2(X_{rd}-X_{cd})^2}& \mbox{for COEF=DIAGONAL:}\\ & \text {weighted Euclidean distance} \end{cases} \]

Partition indexes are

\[ \begin{array}{llll} P_{rcs} & = & 1 & \mbox{for CONDITION=UN} \\ & = & s & \mbox{for CONDITION=MATRIX} \\ & = & (s-1)N+r & \mbox{for CONDITION=ROW} \end{array} \]

The estimated transformation for each partition is

\[ \begin{array}{llll} T_ p(d) & = & d & \mbox{for LEVEL=ABSOLUTE} \\ & = & B_ pd & \mbox{for LEVEL=RATIO} \\ & = & A_ p+B_ pd & \mbox{for LEVEL=INTERVAL} \\ & = & B_ pd^{C_ p} & \mbox{for LEVEL=LOGINTERVAL} \end{array} \]

For LEVEL=ORDINAL, $T_{p}({\cdot })$ is computed as a least-squares monotone transformation.

For LEVEL=ABSOLUTE, RATIO, or INTERVAL, the residuals are computed as

\begin{eqnarray*} Q_{rcs} & =& O_{rcs} \\ R_{rcs} & =& Q_{rcs}^ f - [T_{P_{rcs}}(D_{rcs})]^ f \end{eqnarray*}

For LEVEL=ORDINAL, the residuals are computed as

\begin{eqnarray*} Q_{rcs} & =& T_{P_{rcs}}(O_{rcs}) \\ R_{rcs} & =& Q_{rcs}^ f - D_{rcs}^ f \end{eqnarray*}

If f is 0, then natural logarithms are used in place of the fth powers.

For each partition, let

\[ U_ p = \frac{\displaystyle {\sum _{r,c,s}F_{rcs}}}{\displaystyle {\sum _{r,c,s | P_{rcs}=p}F_{rcs}}} \]

and

\[ \overline{Q}_ p = \frac{\displaystyle {\sum _{r,c,s | P_{rcs}=p}Q_{rcs}F_{rcs}}}{\displaystyle {\sum _{r,c,s | P_{rcs}=p}F_{rcs}}} \]

Then the standardization factor for each partition is

\[ \begin{array}{llll} S_ p & =& 1 & \mbox{for FORMULA=0} \\ & =& U_ p \displaystyle {\sum _{r,c,s | P_{rcs}=p} Q_{rcs}^2F_{rcs} } & \mbox{for FORMULA=1} \\ & =& U_ p \displaystyle {\sum _{r,c,s | P_{rcs}=p} (Q_{rcs}-\overline{Q}_ p)^2F_{rcs} } & \mbox{for FORMULA=2} \end{array} \]

The badness-of-fit criterion that the MDS procedure tries to minimize is

\[ \sqrt {\displaystyle {\sum _{r,c,s} \frac{R_{rcs}^2 F_{rcs} }{S_{P_{rcs}}} } } \]