Introduction to Statistical Modeling with SAS/STAT Software
A class of models that has gained increasing importance in the past several decades is the class of generalized linear models. The theory of generalized linear models originated with Nelder and Wedderburn (1972); Wedderburn (1974), and was subsequently made popular in the monograph by McCullagh and Nelder (1989). This class of models extends the theory and methods of linear models to data with nonnormal responses. Before this theory was developed, modeling of nonnormal data typically relied on transformations of the data, and the transformations were chosen to improve symmetry, homogeneity of variance, or normality. Such transformations have to be performed with care because they also have implications for the error structure of the model, Also, back-transforming estimates or predicted values can introduce bias.
Generalized linear models also apply a transformation, known as the link function, but it is applied to a deterministic component, the mean of the data. Furthermore, generalized linear models take the distribution of the data into account, rather than assuming that a transformation of the data leads to normally distributed data to which standard linear modeling techniques can be applied.
To put this generalization in place requires a slightly more sophisticated model setup than that required for linear models for normal data:
-
The systematic component is a linear predictor similar to that in linear models,
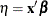 . The linear predictor is a linear function in the parameters. In contrast to the linear model,
. The linear predictor is a linear function in the parameters. In contrast to the linear model, 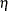 does not represent the mean function of the data.
does not represent the mean function of the data.
-
The link function
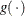 relates the linear predictor to the mean,
relates the linear predictor to the mean, 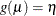 . The link function is a monotonic, invertible function. The mean can thus be expressed as the inversely linked linear predictor,
. The link function is a monotonic, invertible function. The mean can thus be expressed as the inversely linked linear predictor,
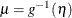 . For example, a common link function for binary and binomial data is the logit link,
. For example, a common link function for binary and binomial data is the logit link, 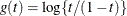 . The mean function of a generalized linear model with logit link and a single regressor can thus be written as
. The mean function of a generalized linear model with logit link and a single regressor can thus be written as
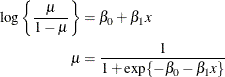
This is known as a logistic regression model.
-
The random component of a generalized linear model is the distribution of the data, assumed to be a member of the exponential family of distributions. Discrete members of this family include the Bernoulli (binary), binomial, Poisson, geometric, and negative binomial (for a given value of the scale parameter) distribution. Continuous members include the normal (Gaussian), beta, gamma, inverse Gaussian, and exponential distribution.
The standard linear model with normally distributed error is a special case of a generalized linear model; the link function is the identity function and the distribution is normal.