Introduction to Statistical Modeling with SAS/STAT Software

Fixed, Random, and Mixed Models

Each term in a statistical model represents either a fixed effect or a random effect. Models in which all effects are fixed are called fixed-effects models. Similarly, models in which all effects are random—apart from possibly an overall intercept term—are called random-effects models. Mixed models, then, are those models that have fixed-effects and random-effects terms. In matrix notation, the linear fixed, linear random, and linear mixed model are represented by the following model equations, respectively:

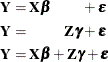
\begin{align*} \bY & = \bX \bbeta \phantom{ + \mb{Z}\bgamma } \, + \bepsilon \\ \bY & = \phantom{\bX \bbeta +}\, \mb{Z}\bgamma + \bepsilon \\ \bY & = \bX \bbeta + \mb{Z}\bgamma + \bepsilon \end{align*}

In these expressions, $\bX $ and $\bZ $ are design or regressor matrices associated with the fixed and random effects, respectively. The vector $\bbeta $ is a vector of fixed-effects parameters, and the vector $\bgamma $ represents the random effects. The mixed modeling procedures in SAS/STAT software assume that the random effects $\bgamma $ follow a normal distribution with variance-covariance matrix $\bG $ and, in most cases, that the random effects have mean zero.

Random effects are often associated with classification effects, but this is not necessary. As an example of random regression effects, you might want to model the slopes in a growth model as consisting of two components: an overall (fixed-effects) slope that represents the slope of the average individual, and individual-specific random deviations from the overall slope. The $\bX $ and $\bZ $ matrix would then have column entries for the regressor variable associated with the slope. You are modeling fixed and randomly varying regression coefficients.

Having random effects in your model has a number of important consequences:

  • Some observations are no longer uncorrelated but instead have a covariance that depends on the variance of the random effects.

  • You can and should distinguish between the inference spaces; inferences can be drawn in a broad, intermediate, and narrow inference space. In the narrow inference space, conclusions are drawn about the particular values of the random effects selected in the study. The broad inference space applies if inferences are drawn with respect to all possible levels of the random effects. The intermediate inference space can be applied for effects consisting of more than one random term, when inferences are broad with respect to some factors and narrow with respect to others. In fixed-effects models, there is no corresponding concept to the broad and intermediate inference spaces.

  • Depending on the structure of 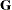$\bG $ and $\mr{Var}[\bepsilon ]$ and also subject to the balance in your data, there might be no closed-form solution for the parameter estimates. Although the model is linear in 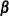$\bbeta $, iterative estimation methods might be required to estimate all parameters of the model.

  • Certain concepts, such as least squares means and Type III estimable functions, are meaningful only for fixed effects.

  • By using random effects, you are modeling variation through variance. Variation in data simply implies that things are not equal. Variance, on the other hand, describes a feature of a random variable. Random effects in your model are random variables: they model variation through variance.

It is important to properly determine the nature of the model effects as fixed or random. An effect is either fixed or random by its very nature; it is improper to consider it fixed in one analysis and random in another depending on what type of results you want to produce. If, for example, a treatment effect is random and you are interested in comparing treatment means, and only the levels selected in the study are of interest, then it is not appropriate to model the treatment effect as fixed so that you can draw on least squares mean analysis. The appropriate strategy is to model the treatment effect as random and to compare the solutions for the treatment effects in the narrow inference space.

In determining whether an effect is fixed or random, it is helpful to inquire about the genesis of the effect. If the levels of an effect are randomly sampled, then the effect is a random effect. The following are examples:

  • In a large clinical trial, drugs A, B, and C are applied to patients in various clinical centers. If the clinical centers are selected at random from a population of possible clinics, their effect on the response is modeled with a random effect.

  • In repeated measures experiments with people or animals as subjects, subjects are declared to be random because they are selected from the larger population to which you want to generalize.

  • Fertilizers could be applied at a number of levels. Three levels are randomly selected for an experiment to represent the population of possible levels. The fertilizer effects are random effects.

Quite often it is not possible to select effects at random, or it is not known how the values in the data became part of the study. For example, suppose you are presented with a data set consisting of student scores in three school districts, with four to ten schools in each district and two to three classrooms in each school. How do you decide which effects are fixed and which are random? As another example, in an agricultural experiment conducted in successive years at two locations, how do you decide whether location and year effects are fixed or random? In these situations, the fixed or random nature of the effect might be debatable, bearing out the adage that "one modeler’s fixed effect is another modeler’s random effect." However, this fact does not constitute license to treat as random those effects that are clearly fixed, or vice versa.

When an effect cannot be randomized or it is not known whether its levels have been randomly selected, it can be a random effect if its impact on the outcome variable is of a stochastic nature—that is, if it is the realization of a random process. Again, this line of thinking relates to the genesis of the effect. A random year, location, or school district effect is a placeholder for different environments that cannot be selected at random but whose effects are the cumulative result of many individual random processes. Note that this argument does not imply that effects are random because the experimenter does not know much about them. The key notion is that effects represent something, whether or not that something is known to the modeler. Broadening the inference space beyond the observed levels is thus possible, although you might not be able to articulate what the realizations of the random effects represent.

A consequence of having random effects in your model is that some observations are no longer uncorrelated but instead have a covariance that depends on the variance of the random effect. In fact, in some modeling applications random effects might be used not only to model heterogeneity in the parameters of a model, but also to induce correlations among observations. The typical assumption about random effects in SAS/STAT software is that the effects are normally distributed.

For more information about mixed modeling tools in SAS/STAT software, see Chapter 6: Introduction to Mixed Modeling Procedures.