The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
You can use the GENMOD procedure to fit a variety of statistical models. A typical use of PROC GENMOD is to perform Poisson regression.
You can use the Poisson distribution to model the distribution of cell counts in a multiway contingency table. Aitkin et al. (1989) have used this method to model insurance claims data. Suppose the following hypothetical insurance claims data are classified by two factors: age group (with two levels) and car type (with three levels).
data insure; input n c car$ age; ln = log(n); datalines; 500 42 small 1 1200 37 medium 1 100 1 large 1 400 101 small 2 500 73 medium 2 300 14 large 2 ;
In the preceding data set, the variable n represents the number of insurance policyholders and the variable c represents the number of insurance claims. The variable car is the type of car involved (classified into three groups) and the variable age is the age group of a policyholder (classified into two groups).
You can use PROC GENMOD to perform a Poisson regression analysis of these data with a log link function. This type of model is sometimes called a log-linear model.
Assume that the number of claims c has a Poisson probability distribution and that its mean, ![]() , is related to the factors
, is related to the factors car and age for observation i by
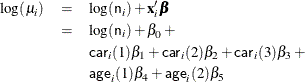
The indicator variables ![]() and
and ![]() are associated with the jth level of the variables
are associated with the jth level of the variables car and age for observation i
The ![]() s are unknown parameters to be estimated by the procedure. The logarithm of the variable
s are unknown parameters to be estimated by the procedure. The logarithm of the variable n is used as an offset—that is, a regression variable with a constant coefficient of 1 for each observation. A log-linear relationship between the mean
and the factors car and age is specified by the log link function. The log link function ensures that the mean number of insurance claims for each car
and age group predicted from the fitted model is positive.
The following statements invoke the GENMOD procedure to perform this analysis:
proc genmod data=insure;
class car age;
model c = car age / dist = poisson
link = log
offset = ln;
run;
The variables car and age are specified as CLASS variables so that PROC GENMOD automatically generates the indicator variables associated with car and age.
The MODEL statement specifies c as the response variable and car and age as explanatory variables. An intercept term is included by default. Thus, the model matrix ![]() (the matrix that has as its ith row the transpose of the covariate vector for the ith observation) consists of a column of 1s representing the intercept term and columns of 0s and 1s derived from indicator
variables representing the levels of the
(the matrix that has as its ith row the transpose of the covariate vector for the ith observation) consists of a column of 1s representing the intercept term and columns of 0s and 1s derived from indicator
variables representing the levels of the car and age variables.
That is, the model matrix is
![\[ \mb{X} = \left[ \begin{array}{r|rrr|rr} 1& 1& 0& 0& 1& 0 \\ 1& 0& 1& 0& 1& 0 \\ 1& 0& 0& 1& 1& 0 \\ 1& 1& 0& 0& 0& 1 \\ 1& 0& 1& 0& 0& 1 \\ 1& 0& 0& 1& 0& 1 \end{array} \right] \]](images/statug_genmod0039.png)
where the first column corresponds to the intercept, the next three columns correspond to the variable car, and the last two columns correspond to the variable age.
The response distribution is specified as Poisson, and the link function is chosen to be log. That is, the Poisson mean parameter
![]() is related to the linear predictor by
is related to the linear predictor by
The logarithm of n is specified as an offset variable, as is common in this type of analysis. In this case, the offset variable serves to normalize
the fitted cell means to a per-policyholder basis, since the total number of claims, not individual policyholder claims, is
observed. PROC GENMOD produces the following default output from the preceding statements.
The "Model Information" table displayed in Figure 43.1 provides information about the specified model and the input data set.
Figure 43.2 displays the "Class Level Information" table, which identifies the levels of the classification variables that are used in
the model. Note that car is a character variable, and the values are sorted in alphabetical order. This is the default sort order, but you can select
different sort orders with the ORDER=
option in the PROC GENMOD statement.
Figure 43.3: Goodness of Fit
| Criteria For Assessing Goodness Of Fit | |||
|---|---|---|---|
| Criterion | DF | Value | Value/DF |
| Deviance | 2 | 2.8207 | 1.4103 |
| Scaled Deviance | 2 | 2.8207 | 1.4103 |
| Pearson Chi-Square | 2 | 2.8416 | 1.4208 |
| Scaled Pearson X2 | 2 | 2.8416 | 1.4208 |
| Log Likelihood | 837.4533 | ||
| Full Log Likelihood | -16.4638 | ||
| AIC (smaller is better) | 40.9276 | ||
| AICC (smaller is better) | 80.9276 | ||
| BIC (smaller is better) | 40.0946 | ||
The "Criteria For Assessing Goodness Of Fit" table displayed in Figure 43.3 contains statistics that summarize the fit of the specified model. These statistics are helpful in judging the adequacy of a model and in comparing it with other models under consideration. If you compare the deviance of 2.8207 with its asymptotic chi-square with 2 degrees of freedom distribution, you find that the p-value is 0.24. This indicates that the specified model fits the data reasonably well.
Figure 43.4: Analysis of Parameter Estimates
| Analysis Of Maximum Likelihood Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | -1.3168 | 0.0903 | -1.4937 | -1.1398 | 212.73 | <.0001 | |
| car | large | 1 | -1.7643 | 0.2724 | -2.2981 | -1.2304 | 41.96 | <.0001 |
| car | medium | 1 | -0.6928 | 0.1282 | -0.9441 | -0.4414 | 29.18 | <.0001 |
| car | small | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| age | 1 | 1 | -1.3199 | 0.1359 | -1.5863 | -1.0536 | 94.34 | <.0001 |
| age | 2 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | |||
| Note: | The scale parameter was held fixed. |
Figure 43.4 displays the "Analysis Of Parameter Estimates" table, which summarizes the results of the iterative parameter estimation process. For each parameter in the model, PROC GENMOD displays columns with the parameter name, the degrees of freedom associated with the parameter, the estimated parameter value, the standard error of the parameter estimate, the confidence intervals, and the Wald chi-square statistic and associated p-value for testing the significance of the parameter to the model. If a column of the model matrix corresponding to a parameter is found to be linearly dependent, or aliased, with columns corresponding to parameters preceding it in the model, PROC GENMOD assigns it zero degrees of freedom and displays a value of zero for both the parameter estimate and its standard error.
This table includes a row for a scale parameter, even though there is no free scale parameter in the Poisson distribution. See the section Response Probability Distributions for the form of the Poisson probability distribution. PROC GENMOD allows the specification of a scale parameter to fit overdispersed Poisson and binomial distributions. In such cases, the SCALE row indicates the value of the overdispersion scale parameter used in adjusting output statistics. See the section Overdispersion for more about overdispersion and the meaning of the SCALE parameter output by the GENMOD procedure. PROC GENMOD displays a note indicating that the scale parameter is fixed—that is, not estimated by the iterative fitting process.
It is usually of interest to assess the importance of the main effects in the model. Type 1 and Type 3 analyses generate statistical tests for the significance of these effects. You can request these analyses with the TYPE1 and TYPE3 options in the MODEL statement, as follows:
proc genmod data=insure;
class car age;
model c = car age / dist = poisson
link = log
offset = ln
type1
type3;
run;
The results of these analyses are summarized in the figures that follow.
In the table for Type 1 analysis displayed in Figure 43.5, each entry in the deviance column represents the deviance for the model containing the effect for that row and all effects
preceding it in the table. For example, the deviance corresponding to car in the table is the deviance of the model containing an intercept and car. As more terms are included in the model, the deviance decreases.
Entries in the chi-square column are likelihood ratio statistics for testing the significance of the effect added to the model
containing all the preceding effects. The chi-square value of 67.69 for car represents twice the difference in log likelihoods between fitting a model with only an intercept term and a model with an
intercept and car. Since the scale parameter is set to 1 in this analysis, this is equal to the difference in deviances. Since two additional
parameters are involved, this statistic can be compared with a chi-square distribution with two degrees of freedom. The resulting
p-value (labeled Pr>Chi) of less than 0.0001 indicates that this variable is highly significant. Similarly, the chi-square
value of 104.64 for age represents the difference in log likelihoods between the model with the intercept and car and the model with the intercept, car, and age. This effect is also highly significant, as indicated by the small p-value.
The Type 3 analysis results in the same conclusions as the Type 1 analysis. The Type 3 chi-square value for the car variable, for example, is twice the difference between the log likelihood for the model with the variables Intercept, car, and age included and the log likelihood for the model with the car variable excluded. The hypothesis tested in this case is the significance of the variable car given that the variable age is in the model. In other words, it tests the additional contribution of car in the model.
The values of the Type 3 likelihood ratio statistics for the car and age variables indicate that both of these factors are highly significant in determining the claims performance of the insurance
policyholders.